1.   引言

随着电子战与信息化战争形态的不断演进，雷达系统作为战场态势感知的核心装备，其任务调度的效率直接影响作战指挥的精确性和响应迅捷性^[1]。雷达体制的发展使得雷达资源管理自由度和灵活性不断提升^[2]。对于岸基雷达而言，要有效应对海空作战的复杂需求，就需要提升其搜索、识别、跟踪、引导、制导以及侦察和抗干扰等多种能力^[3]。在处理海上任务时，由于海上目标具有种类多、数量大、分布密集、速度慢、动态性强等特点，任务的生成一般依靠战术和人工规则，雷达体系整体作战能力不足^[4]。这些任务生成后各自带有不同的优先级和时效要求^[5,6]，单个任务可能需要多个雷达发射不同波段的信号来协同完成^[7]，任务之间还存在着复杂的约束关系。因此，如何科学合理地分配雷达资源，从时间资源管理角度出发，在约束条件范围内确定任务调度顺序^[8]，保障关键任务的优先执行，构成了多雷达协同任务调度问题的核心。文献[9]已证实，针对带有时间窗约束的单雷达调度问题，其本质上属于NP-Hard问题，求解过程极具挑战性。相比之下，当问题扩展到包含时间窗及多种约束条件的多雷达协同调度时，其求解的复杂性更是显著提升，难度进一步加大。并且，复杂约束条件下，调度如果只考虑某一个阶段的任务情况，容易陷入局部最优。如何使算法可以根据问题动态地调整策略，把握全局信息，在合理的求解时间内提升整体的调度效果非常重要。

为了解决雷达任务调度问题，研究者提出了多种调度策略，文献[5]采用规则调度方法，根据任务的重要性和紧急性为任务分配优先级，根据优先级规则进行任务排布，可以在较短的时间内提供解决方案。文献[10]对影响单机雷达截获目标的关键因素采取多属性决策方法进行任务规划。文献[11]研究了基于综合优先级的任务规划方法。文献[12]引入了时间指针来指示何时选择具有最高综合优先级的波束驻留任务。以上方法均是基于规则进行调度，有其特定的适用场景，总体来说该类方法并不具有普适性，无法兼顾多方面的性能指标。目前，调度策略已由此类模板式的调度策略向自适应方向转变。

数学规划方法是典型的精确优化方法，文献[13]将任务节点聚合形成分支，通过筛掉收益较低的分支来提升求解效率。文献[14]将多雷达协同任务分配问题建模成多变量混合整数规划优化问题，用启发式穷举法和凸松弛两步解耦算法进行求解。文献[15]针对组网雷达多目标跟踪资源分配优化问题，采用两步分解法，结合半正定规划算法和循环最小算法对问题进行求解。文献[16]针对分布式组网雷达场景，建立了波束分配和驻留时间联合优化模型，采用基于奖励的迭代下降搜索算法求解资源在多目标间的分配问题。文献[17]建立了相控阵雷达任务的二次规划数学模型，证明了其最优解的存在性，但也侧面说明了调度问题最优解求解的难度。雷达调度问题本身是NP-Hard问题，随着问题规模的增加，求解难度会显著增高。近似方法旨在在可接受的时间范围内找到接近最优解的解。为了解决MIMO雷达任务调度与资源分配问题，文献[18]建立了抢占式单机雷达任务优化调度模型，提出了一种新的启发式任务交错调度算法，文献[19]将混合粒子群优化和Levy飞行结合来求解MIMO雷达任务调度优化模型，并在文献[20]中将整数规划和混合粒子群算法进行了结合，兼具探索性的同时提升了多方面的性能，此类方法对于非抢占式多雷达协同任务调度问题仍具有参考意义。文献[21]将时间分割成多个时间窗口，根据任务特性和当前任务饱和度为不同任务分配特定的时间段。文献[22]将多目标车间调度问题转化为单目标优化问题，用混合差分进化算法进行求解，车间调度问题与多雷达协同问题存在共同之处，但是没有考虑到机器之间的协作和任务之间的约束条件。文献[6]基于背包问题对相控阵雷达的功率和时间资源进行了规划，使雷达可以在有限时间内跟踪更多目标。文献[23]根据雷达启动准备时间和完全准备时间构造折扣因子，通过拍卖机制，对时效性受限的任务进行调度。上述启发式的近似方法求解复杂度低，但是存在缺乏全局优化能力的缺点，且对任务复杂约束关注较少，不能直接适用于岸基雷达任务调度场景。

随着人工智能和机器学习技术的发展，针对雷达任务调度问题的研究也在不断进步。在调度的监督学习方法中，支持向量机^[24]和神经网络方法可以用来对现有调度方法进行选择，也可以学习新的调度规则^[25]。文献[26]对小规模样本进行离线计算得到标签，通过卷积神经网络进行了监督学习。最优的样本标签通常很难获得，相比之下，强化学习^[27]、多智能体系统^[28]等方法具有自主学习能力，可以开发出更加智能和自适应性的调度算法。文献[29]在强化学习过程中根据奖惩策略迭代地改变任务优先级，将选出的最佳任务传递给最早开始时间算法进行调度。深度强化学习是强化学习和深度学习的结合^[30]，文献[31]采用深度强化学习方法解决了伴随压制干扰下的组网雷达功率分配博弈问题。使用深度学习网络自动学习数据，提取复杂而有用的特征，为智能体提供了更为丰富全面的环境感知能力。从技术发展和应用需求角度来看，数学建模和人工智能相结合的协同调度方法是未来的重要发展趋势^[7]。

在当前复杂多变的雷达任务调度场景中，传统规则调度方法已显局限，而数学模型求解方法因其高复杂度难以迅速获取可行解。尽管神经网络学习方法具备高效求解和低复杂度的优势，但其对特征的全覆盖需求却对网络构成挑战。为应对雷达任务调度中的复杂约束与高效求解需求，本文提出了一种融合模型知识与图神经网络的方法。首先，本文设计了一种异构图结构，用于精确表述雷达任务间的约束关系以及雷达与任务之间的关联信息。基于这一图结构，构建了拉普拉斯矩阵，并通过谱分析提出了全局信息的有效计算方法，创新性地实现了对问题特征的全面覆盖。此图结构具备灵活性，可适应不同规模问题的求解，使得算法具备快速求解复杂问题的能力。为了有效提取和嵌入图中的节点特征，采用了图卷积神经网络，并在此基础上设计了策略网络，采用了近端策略优化方法对网络进行训练，并提出了由问题引导解和经验解构成的上下界信息来减少决策空间大小的方法，使求解更为高效。实验结果表明，本文所提出的方法不仅训练效率高，在调度效果上显著优于其他调度方法，且关注到了任务之间的约束关系，展现了对不同规模雷达任务调度问题的强大适应性。

2.   多雷达协同任务调度问题模型

假设当前雷达网络中包含多部高性能雷达，每台雷达配备了不同的波束波段，通过协同的方式共同承担监测区域内的搜索、多目标跟踪、定位、打击等任务。雷达系统中，系统前端和处理模块会按照设定的程序进行数据交换，任务生成模块根据返回数据情况，形成波束驻留调度任务请求，在调度资源的约束条件下，生成下一个调度间隔内各个雷达节点的波束驻留任务列表^[32]。任务调度的目标是在有限的资源下最大化任务调度的成功率。

基于雷达任务实现的实际业务流程，定义如下约束和假设。

(1) 任务的不可抢占性：系统中的每个实时任务均直接关联特定的雷达波束和传感器，这些雷达需要在特定的方向上进行一段时间的连续观测，因此，在驻留期间任务不会被其他任务所打断或中断。

(2) 优先约束：任务之间存在先后约束。例如在单雷达检测跟踪识别任务中，首先需经由检测跟踪任务实现目标起批，随后才能对起批目标实现逐批次识别。

(3) 同步约束：对于多雷达协同调度场景，某些任务必须在不同的雷达上同步执行，例如在多波段雷达检测跟踪任务中，为提升雷达检测跟踪及抗干扰性能，由不同波段雷达传感器同步执行目标检测跟踪任务后，才能实现后续的目标融合。采用任务分解方法，将一个需要多雷达协同完成的任务视作多个子任务的集合，每个子任务由对应的单个雷达执行，子任务之间定义同步执行约束。

(4) 截止时间约束：所有任务必须在截止期之前完成，否则该任务调度失败。

为更好地描述模型，首先给出一些符号定义：$ {{\boldsymbol{T}}} $为全部任务集合。$ {N} $为任务个数。将多雷达协同任务分解为多个单雷达子任务集合，每个子任务在建模时当作一个单独的任务处理。$ {{\boldsymbol{M}}} $表示全部雷达集合。$ {{{\boldsymbol{T}}}}_{{m}} $表示在雷达$ {m} $上待处理的任务集，$ {T}{=} {{\cup }}_{{m}{\in}{{\boldsymbol{M}}}}{\boldsymbol{T}}_{{m}} $。$ {i,j}\in {{\boldsymbol{T}}} $表示任务$ {i} $和任务$ {j} $。$ {m}{\in}{{\boldsymbol{M}}} $表示雷达$ {m} $，$ {{m}}_{{i}} $表示执行任务$ {i} $的雷达，具有唯一性，即任务$ {i} $由指定的某一个雷达完成。$ {{p}}_{{i}} $表示任务$ {i} $的驻留时间。$ {{r}}_{{i}} $表示任务$ {i} $的释放时间。$ {{x}}_{{i}} $表示任务$ {i} $开始执行时间。$ {{d}}_{{i}} $表示任务$ {i} $截止期。

$ {\boldsymbol{\phi}}_{{i}} $表示惩罚权重，若任务$ {i} $没有被成功调度，则会导致惩罚。$ {\boldsymbol{\phi}}_{{i}} $的设定与任务的优先级有关，如果任务的优先级高，则相应的惩罚因子较大，反之则较小。所以，一个雷达任务实体模型$ {{{\boldsymbol{F}}}}_{{i}} $可用一个三元组表示：

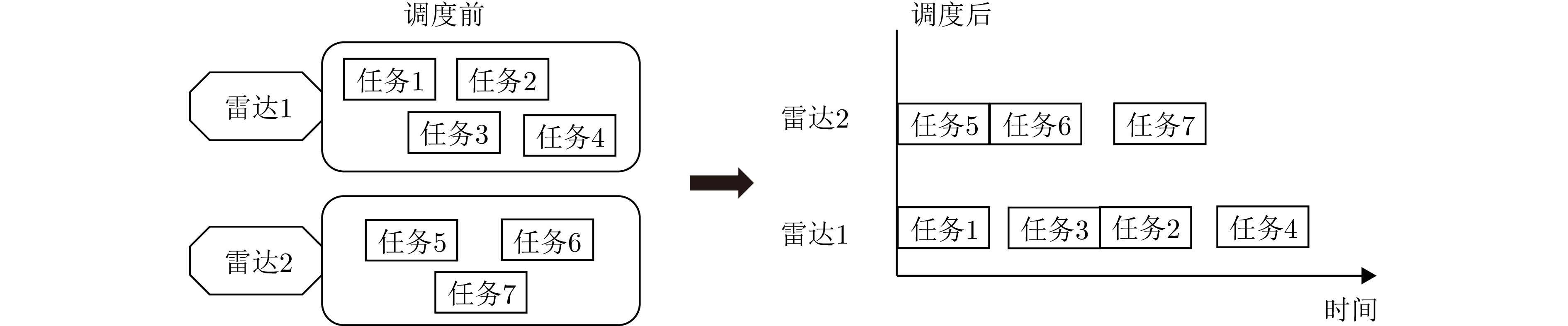
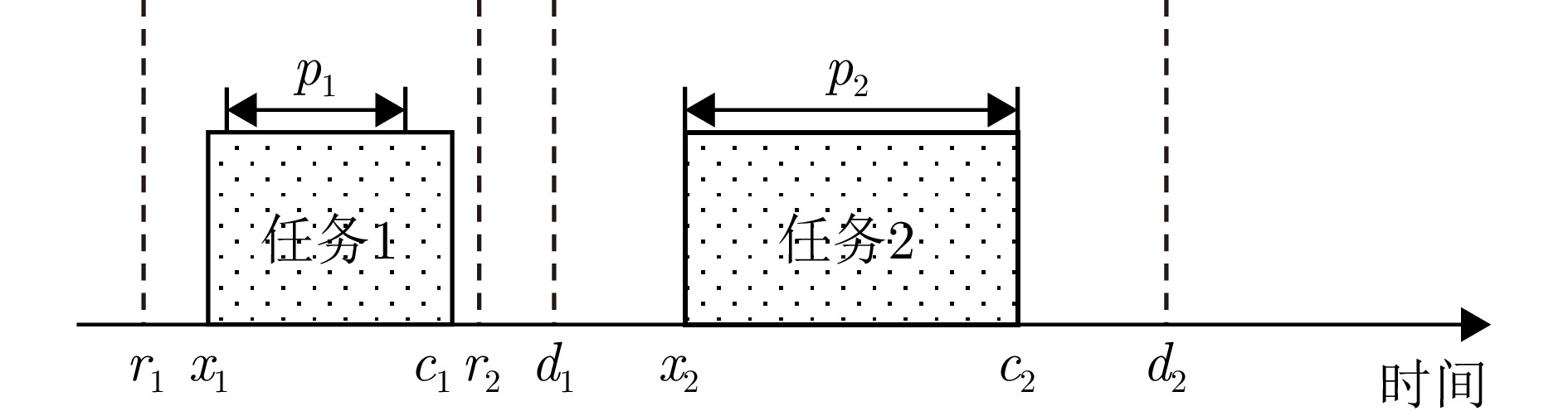
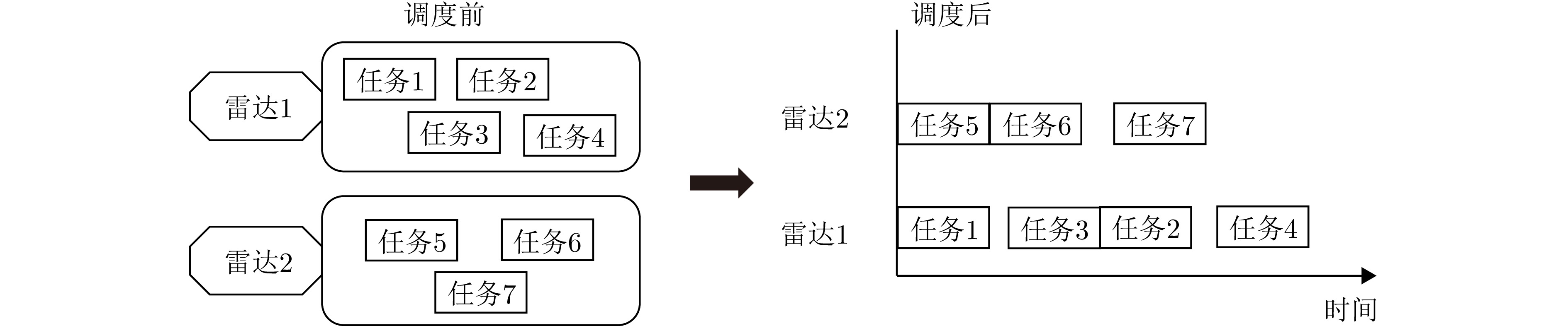
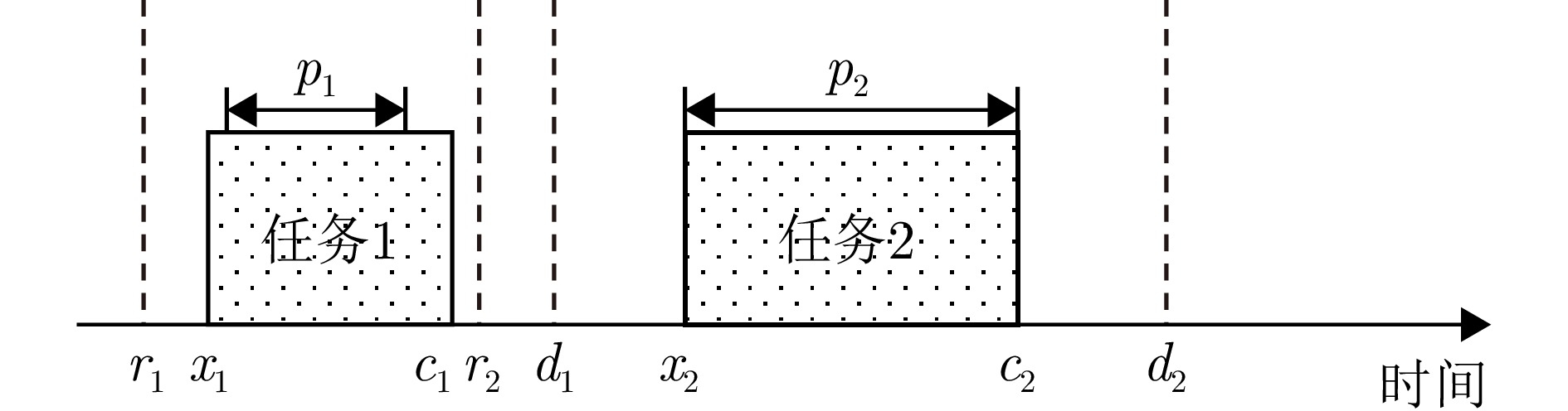
其中，$ \left[{{r}}_{{i}}{}{{d}}_{{i}}\right] $为时间窗。雷达任务在时间轴上的结构表示如图1所示，图2是雷达任务调度的示意图。多雷达协同任务调度问题可归纳为，给定包含多个任务的任务集$ {{\boldsymbol{T}}} $，确定每个任务在各自雷达上的开始执行时间，使得未成功调度任务导致的惩罚成本最小。

图  1  雷达任务结构

Figure  1.  Structure of radar task

下载: 全尺寸图片 幻灯片

图  2  任务调度示意

Figure  2.  Schematic of task scheduling

下载: 全尺寸图片 幻灯片

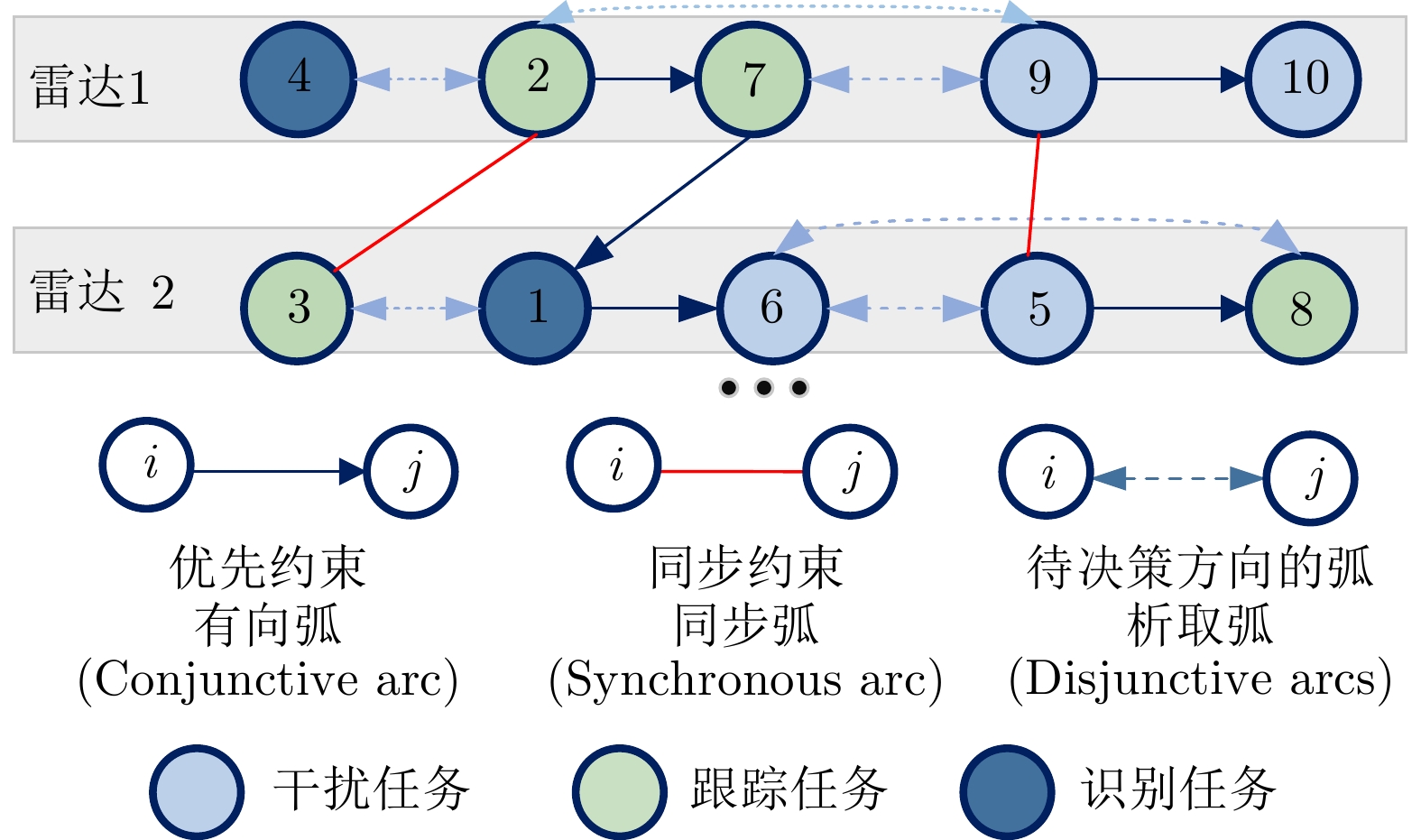
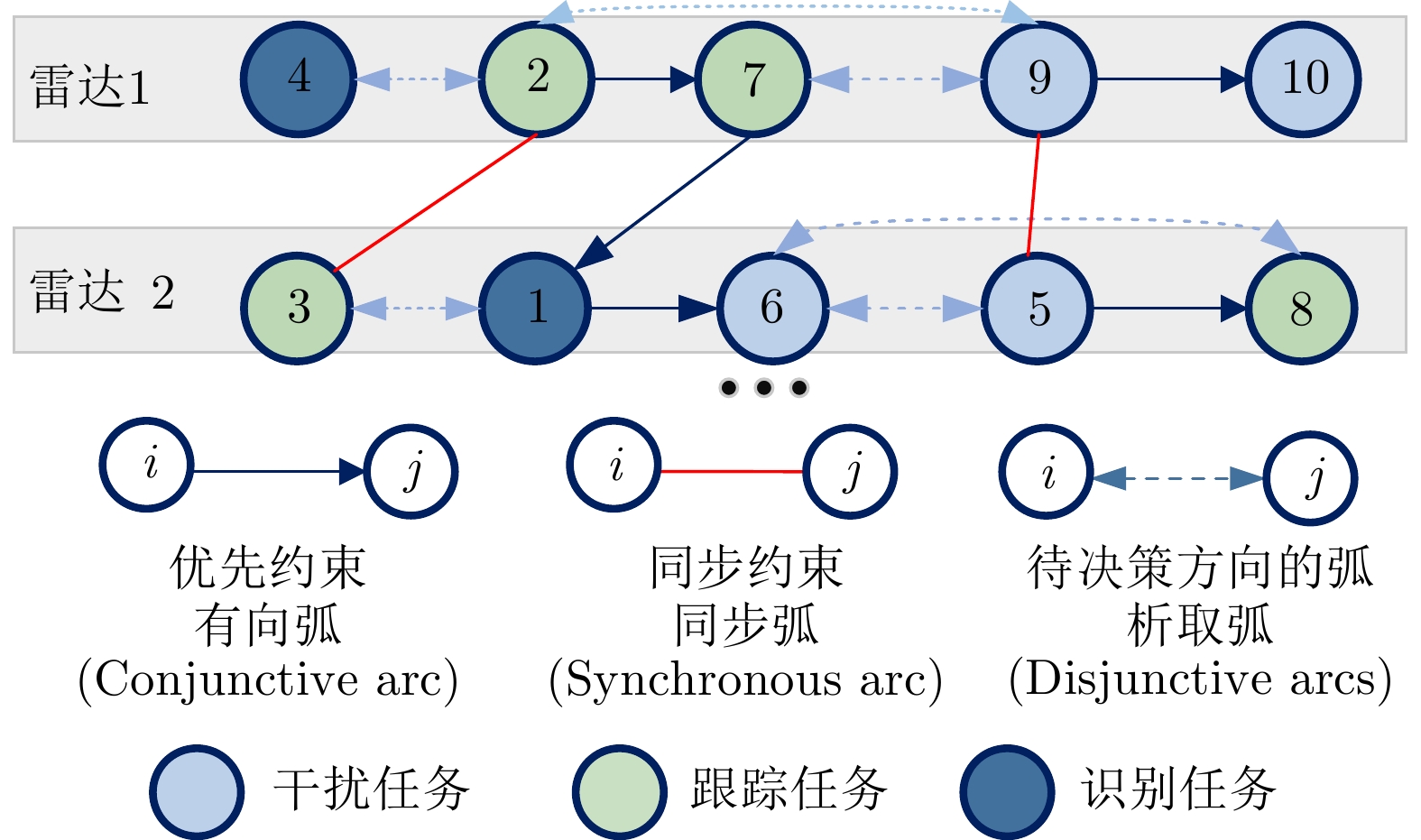
将雷达看作机器资源，任务看作待加工的部件，多雷达任务协同调度问题可以被看作多机器离散加工调度问题，约束条件和决策变量可通过异构图进行建模^[27]。如图3所示，在该示例中，有2部雷达，10个任务，其中雷达1需要处理任务集$ \left\{\mathrm{4,2},\mathrm{7,9},10\right\} $，雷达2需要处理任务集$ \left\{\mathrm{3,1},\mathrm{6,5},8\right\} $。对于优先约束，用确定的有向弧表示，代表任务间的顺序已确定，定义合取弧集为$ {{\boldsymbol{C}}} $。如图3所示，存在有向弧$ \left(7\to 1\right) $，说明任务7必须在任务1之前执行。对于同步约束，用无向弧集$ {{\boldsymbol{S}}} $表示，在图3中存在无向弧$ \left(2-3\right) $，说明任务2必须与任务3同时执行。任务调度的实质是在约束条件下，确定每个任务在对应雷达上的执行顺序，如果两个任务之间没有确定顺序，即可建模为析取弧，析取弧集用$ {{\boldsymbol{D}}} $表示，需要根据优化目标来确定析取弧方向，将析取弧转换为合取弧。当所有的析取弧都确定了方向，任务的调度顺序就确定了，在无等待调度条件下^[9]，所有任务的开始执行时间也将完全确定。

图  3  基于异构图网络的雷达任务调度问题描述

Figure  3.  Description of the radar task scheduling problem based on heterogeneous graph networks

下载: 全尺寸图片 幻灯片

定义$ {{c}}_{{i}} $为任务$ {i} $的完成时间，因此，$ {{c}}_{{i}}{=}{{x}}_{{i}}{+}{{p}}_{{i}} $。

$ {}{ \varepsilon } $表示阶跃函数，$ \varepsilon ({x}){=}\left\{ $$\begin{array}{lllllll}{1},& {x}{\ge}{0}\\{0},& {x}{ < }{0}\end{array}$$ \right. $

定义决策变量为$ {{x}}_{{i}} $，建立如下数学规划模型^[33](FP)：

其中，式(1)为优化目标，即最小化加权调度惩罚，$ {{{\boldsymbol{\phi}}}}_{{i}} $表示当任务$ {i} $调度失败时导致的惩罚值，当$ {{{\boldsymbol{\phi}}}}_{{i}}{=1} $时问题的优化目标也可以看作为求最大调度成功率。约束(2)表示带有优先约束的任务之间的先后顺序约束；约束(3)表示当两个任务由同一台雷达来执行时，它们之间的先后顺序待确定，用析取弧来连接。需要确定这两个任务的先后关系，并且任务之间是非抢占式关系^[34]；约束(4)表示这两个任务需要多个雷达协同处理，且同时开始。

模型FP必定是强NP-hard问题。从计算理论角度看，因为约束(2)和约束(4)的存在使得FP模型存在多雷达的协同，增加了调度的复杂度。即使松弛约束(2)、约束(4)，则FP将退化为$ {m} $个独立的带时间窗的单雷达任务调度，文献[9]证明即使是带时间窗的单雷达任务调度，该问题也是NP-Hard问题，所以FP问题的求解必定会更困难。

3.   基于模型知识融合的图神经网络多雷达协同任务调度算法

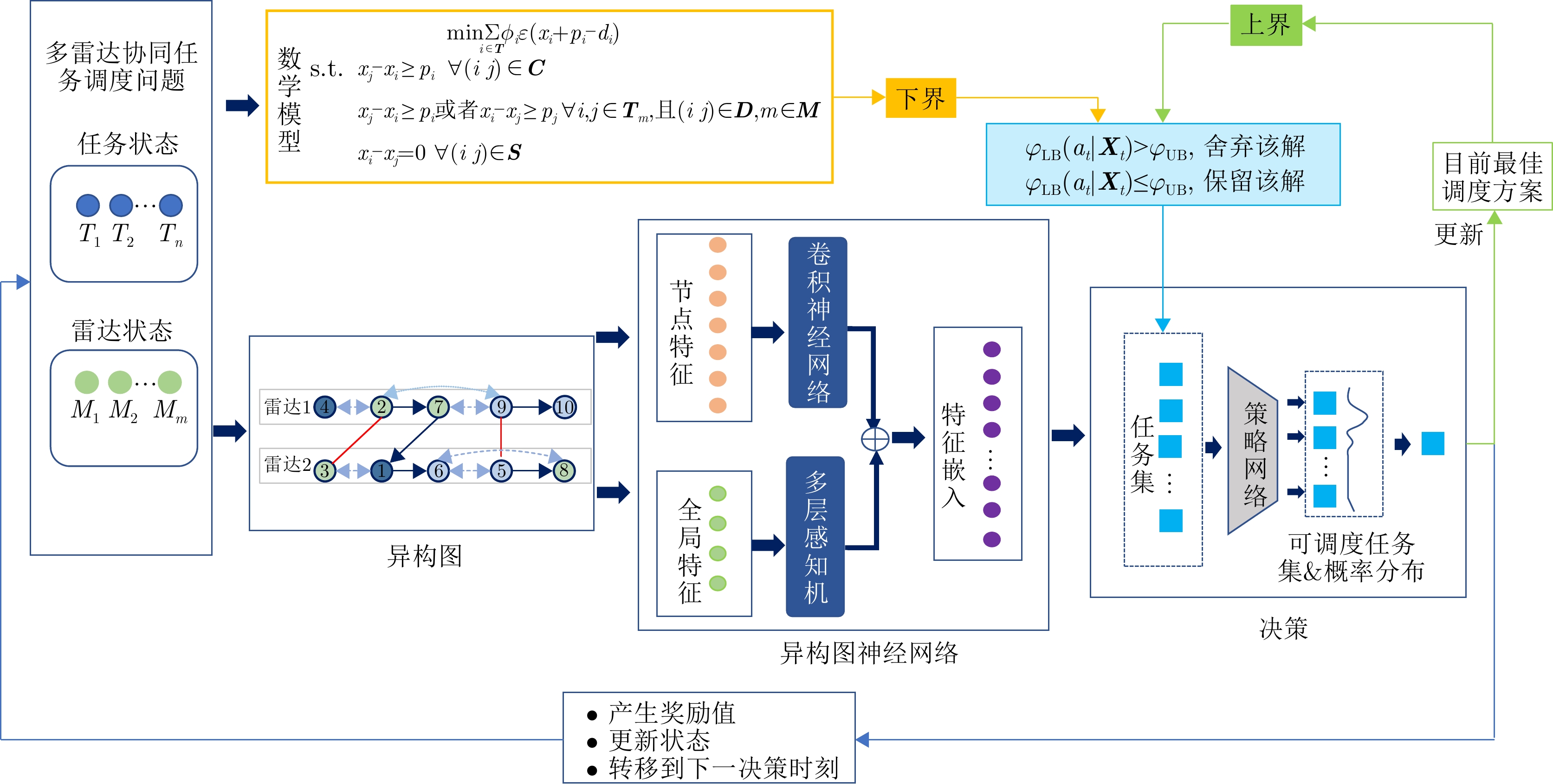
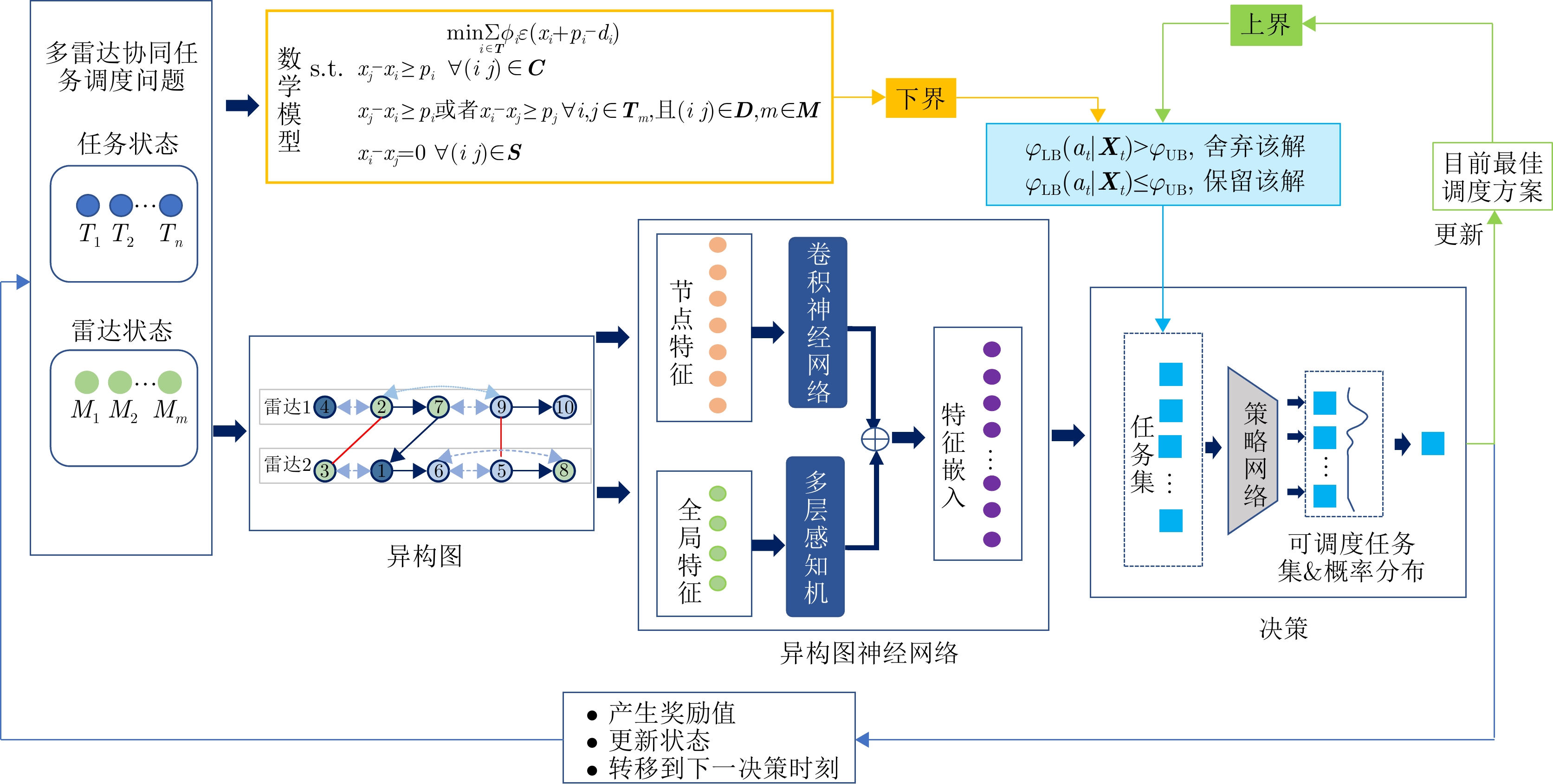
为了解决以上优化问题，本文提出了一种基于模型知识融合的图神经网络多雷达协同任务调度算法(Model Knowledge Embedded Graph Neural Networks, MKEGNN)。该算法首先将多雷达任务协同调度问题建模为异构图模型和数学模型，利用图结构直观展现任务之间的约束关系。为了对图中信息进行全面覆盖，使用两部分图神经网络来分别提取节点特征和全局特征。其中，在全局特征选取部分创新性地提出了随机拉普拉斯矩阵谱特征选取方法。求解调度问题的过程可以认为是一个连续的决策过程，策略的好坏直接影响最终的调度结果。因此采用强化学习中的近端策略优化算法(Proximal Policy Optimization, PPO)来指导决策，进行整体网络训练^[28]。为了提升强化学习的效率，结合问题的数学模型，从松弛数学模型中获取问题的引导解，计算下界信息。利用网络训练过程中的最优解，也即经验解，计算问题的上界信息。上下界信息结合起来对决策任务进行筛选，从而提前筛掉劣质解，提升算法计算效率，同时指导网络朝更优的方向更新。算法的整体架构如图4所示。

图  4  基于模型知识融合的图神经网络框架

Figure  4.  Framework for model knowledge embedded graph neural networks

下载: 全尺寸图片 幻灯片

求解调度问题的过程是一个连续的决策过程，在每个决策步骤$ {t} $(时间为0或者上一步决策完成时)策略网络会根据当前系统状态$ {{{\boldsymbol{S}}}}_{{t}} $做出决策，选出下一步调度的任务$ {{a}}_{{t}} $，环境转移到下一个决策步骤$ {t}{+1} $。该流程迭代，直到所有可调度任务均被调度结束，相应的MDP建模过程如下。

状态：步骤$ {t} $中所有任务的状态构成状态$ {{{\boldsymbol{S}}}}_{{t}} $。动作：基于当前可选任务集$ {{{\boldsymbol{X}}}}_{{t}} $选出下一步调度的任务$ {{a}}_{{t}} $。状态转移：根据状态$ {{{\boldsymbol{S}}}}_{{t}} $和动作$ {{a}}_{{t}} $，环境可以确定性地转移到下一个状态$ {{{\boldsymbol{S}}}}_{{t}{+1}} $，本文通过不同的异构图拓扑结构和特征来区分不同的两种状态。奖励：奖励定义为在状态$ {{{\boldsymbol{S}}}}_{{t}} $和$ {{{\boldsymbol{S}}}}_{{t}{+1}} $下的调度成功率之差$ r\left({{{\boldsymbol{S}}}}_{{t}}{,}{{{a}}_{{t}}{,}{{\boldsymbol{S}}}}_{{t}{+1}}\right){=}{\eta}\left({{{\boldsymbol{S}}}}_{{t}}\right){-}{\eta}\left({{{\boldsymbol{S}}}}_{{t}{+1}}\right) $。策略：策略$ \pi \left({{a}}_{{t}}|{{{\boldsymbol{S}}}}_{{t}}\right) $表示在状态$ {{{\boldsymbol{S}}}}_{{t}} $下，可调度任务集合$ {{{\boldsymbol{X}}}}_{{t}} $上的动作概率分布。

3.1   基于任务节点的特征计算

对每个任务节点$ {i} $，其特点和属性较为固定。参考文献[27]，定义7个维度的任务基本特征，如表1所示。

表  1  基于任务节点的7维度特征嵌入

Table  1.  7-dimensional feature embedding based on task nodes

序号	特征维度	特征说明
1	任务状态$ {\rm{ST}}_{{i}} $	标识任务此前是否被调度过，已调度任务状态为$ {\rm{ST}}_{{i}}=1 $，否则为$ {\rm{ST}}_{{i}}=0 $
2	处理时间$ {{p}}_{{i}} $	雷达资源执行任务所需时间，包括准备时间
3	时间裕度tr	任务的截止期$ {{d}}_{{i}} $与雷达最早可用时间$ {{t}}_{{a}}^{{{m}}_{{i}}} $之差，反映任务的紧急程度
4	任务所关联雷达的未调度任务个数$ {{N}}_{{i}}^{{t}} $	$ {t} $时刻待处理任务队列中，与属于任务$ {i} $同属于雷达$ {{m}}_{{i}} $，且尚未调度的任务的个数
5	权重值$ {{\varphi}}_{{i}} $	与任务优先级相关的权重值
6	入度弧个数$ {{E}}_{{i}} $	表示有向弧中指向任务$ {i} $的弧的个数
7	同步弧个数$ {{{\mathrm{Syn}}}}_{{i}} $	表示与任务$ {i} $同步任务的个数

下载: 导出CSV 

| 显示表格

3.2   基于异构图模型知识的全局特征计算

研究^[5,10,33]普遍认为，待调度任务的参数和约束关系对于调度的成功率影响很大，已有的算法无论是规则型算法还是图神经网络算法，提取的特征要么不够全面，要么过于个性化，泛化性能不强。因此，当调度问题场景的类型发生变化时，算法的稳定性不高。异构图的拓扑结构是图重要的全局信息来源，为挖掘图中的共性全局特征，本文引入拉普拉斯矩阵$ {{\boldsymbol{L}}} $来描述图$ \boldsymbol{G}{=}\left({{\boldsymbol{T}}}{,}{{\boldsymbol{J}}}\right) $的拓扑结构信息，其中，$ {{\boldsymbol{T}}} $为任务集，$ {{\boldsymbol{J}}}{=}{{\boldsymbol{C}}}{\cup}{{\boldsymbol{S}}}{\cup}{{\boldsymbol{D}}} $为所有的弧集。首先计算异构图$ {{\boldsymbol{G}}} $对应的拉普拉斯矩阵，其计算公式为

其中，$ {{\boldsymbol{W}}} $为权重矩阵，其权重表示任务在其前置任务之后执行的最小等待时间，若任务$ {i} $为任务$ {j} $的前置任务，则$ {\boldsymbol{W}}_{{ij}}{=}{{p}}_{{i}} $，其余情况下$ {\boldsymbol{W}}_{{ij}}{=}{0} $。$ {\boldsymbol{D}}_{{e}} $为图的出度矩阵，可以使用奇异值分解技术对拉普拉斯矩阵进行分解：

其中，$ {{\boldsymbol{A}}} $, $ {{\boldsymbol{V}}} $都是酉矩阵，满足$ {{{\boldsymbol{A}}}}^{\rm{H}}{{\boldsymbol{A}}}{=}{{\boldsymbol{A}}}{\boldsymbol{A}}^{\rm{H}}{=}{{\boldsymbol{I}}} $，$ {{\boldsymbol{I}}} $是单位矩阵。$ {\boldsymbol{V}}^{\rm{H}} $是矩阵$ {{\boldsymbol{V}}} $的转置矩阵，$ {{\boldsymbol{ \varSigma}} } $是对角矩阵，对角线数值为$ {{\boldsymbol{L}}} $的实数奇异值^[35]。进而有

为了强化出调度问题的共性特征，基于随机矩阵理论，可以对矩阵进行一定的随机性处理，增添扰动噪声信息，从而提升抗干扰能力，增强算法鲁棒性^[36,37]。对矩阵左乘随机矩阵是数据处理领域常见的矩阵降维手段，可以改变数据表示而不改变内在结构，减小特征计算难度^[38]。如果随机矩阵的维度与原矩阵维度相同，则可以在不改变维度的情况下对原矩阵添加扰动信息，从而模糊掉节点之间的差异，以减少特性因素对调度结果的干扰，关注整体的共性特征^[37,39]。因此，生成随机矩阵$ {{\boldsymbol{P}}}\in {{{\boldsymbol{R}}}}^{{N}{\times}{N}} $，$ {{\boldsymbol{P}}} $中元素$ {{{\boldsymbol{P}}}}_{{ij}} $为0到1之间的随机数，服从均匀独立同分布^[35]。对$ {{\boldsymbol{P}}} $进行分解得到随机酉矩阵

对矩阵$ \sqrt{{{{\boldsymbol{L}}}}^{{{\mathrm{H}}}}{{\boldsymbol{L}}}} $左乘随机酉矩阵$ {{\boldsymbol{U}}} $，

其中，$ {{\boldsymbol{H}}}{=}{{\boldsymbol{UV}}} $也是酉矩阵，$ {{{\boldsymbol{L}}}}_{{u}} $又称为$ {{\boldsymbol{L}}} $的奇异值等价矩阵，有相似的奇异值分布^[37]。

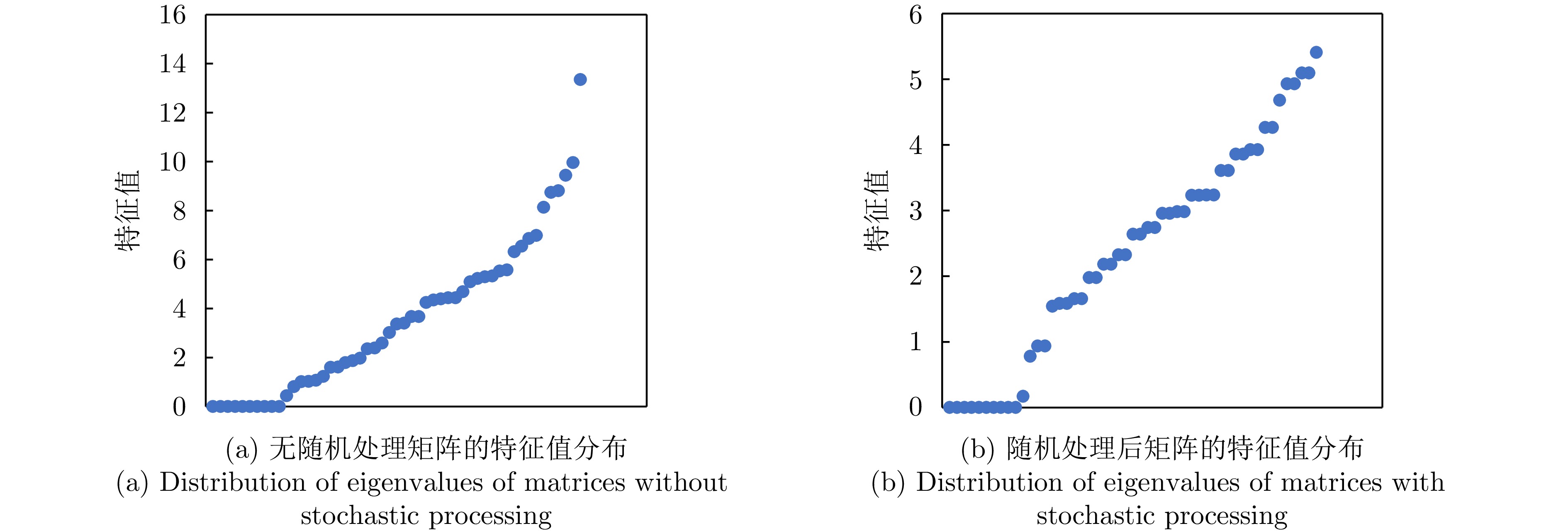
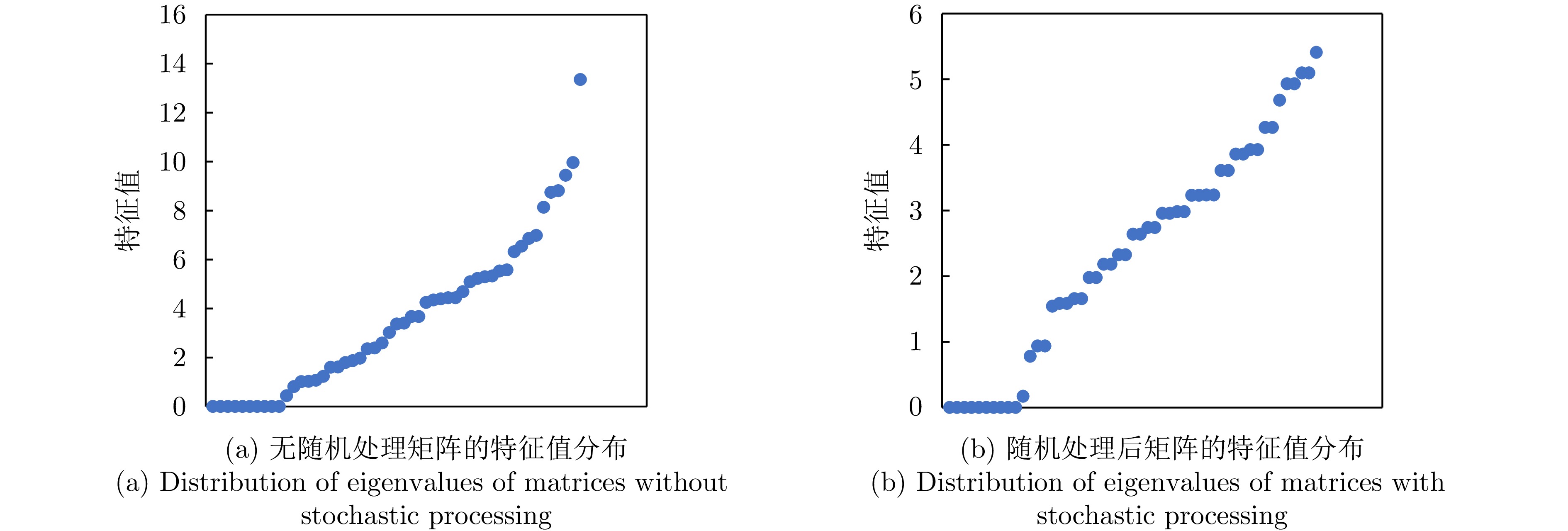
定义平均前置任务个数$ E=\dfrac{1}{N}\displaystyle\sum\nolimits_{i=1}^{N}\left|{E}_{i}\right| $，$ {{E}}_{{i}} $为任务的前置任务的个数。定义处理时间分布标准差$ \sigma {=}\sqrt{\dfrac{{1}}{{N}{-1}}\displaystyle\sum\nolimits _{{i}{=1}}^{{N}}{{(}{{p}}_{{i}}{-}{{{\bar p}}_{{i}}}{)}}^{{2}}} $，$ {{p}}_{{i}} $为任务的驻留时间，$ {{\bar{p}}_{{i}}} $为驻留时间均值。对一个包含50个任务和5台雷达的任务调度实例，改变其平均前置约束个数，构建上述矩阵$ \sqrt{{\boldsymbol{L}}^{\rm{H}}{{\boldsymbol{L}}}} $，对比随机处理前后的特征值的模的变化情况，如图5所示。随机处理后，矩阵的特征值整体规模变小，数值更稳定，有助于提升神经网络算法的稳定性，加速收敛，提升效率。数据内部的结构关系更加清晰，特征值的模的分布情况由处理前的连续均匀分布，转为呈现一定的走势，分布情况更稀疏，有助于在特征选择和降维时保留更为重要的特征。

图  5  随机处理对任务集关系网络特征值分布的影响

Figure  5.  The effect of stochastic processing on the distribution of eigenvalues of task-set relational networks

下载: 全尺寸图片 幻灯片

通过以上分析，将原始的雷达任务关系图的拉普拉斯矩阵映射成一个随机矩阵$ {\boldsymbol{L}}_{{u}} $。为了全面刻画该问题的全局特征，对$ {\boldsymbol{L}}_{{u}} $计算以下4个关键指标^[37]作为问题的全局特征。

(1) 零特征值的个数$ {{n}}_{{0}} $：在物理上反映图中连通区域的个数。

(2) 最小非零特征值$ {{ \lambda }}_{{\min+}} $：在物理上反映图的代数连通度。

(3) 平均谱半径MSR：表征系统宏观情况，对状态变化敏感^[37]，计算公式如下：

其中，$ {{ \lambda }}_{{i}}\left({i}{=1,2,\cdots,}{N}\right) $是矩阵$ {\boldsymbol{L}}_{{u}} $的特征值，$ {{\mathrm{MSR}}} $即为各特征值模的均值。

(4) 谱半径$ {\rho} $，计算公式如下：

其中，$ {{ \lambda }}_{{i}}\left({i}{=1,2,\cdots,}{N}\right) $是矩阵$ {\boldsymbol{L}}_{{u}} $的特征值，谱半径即为特征值的最大值。

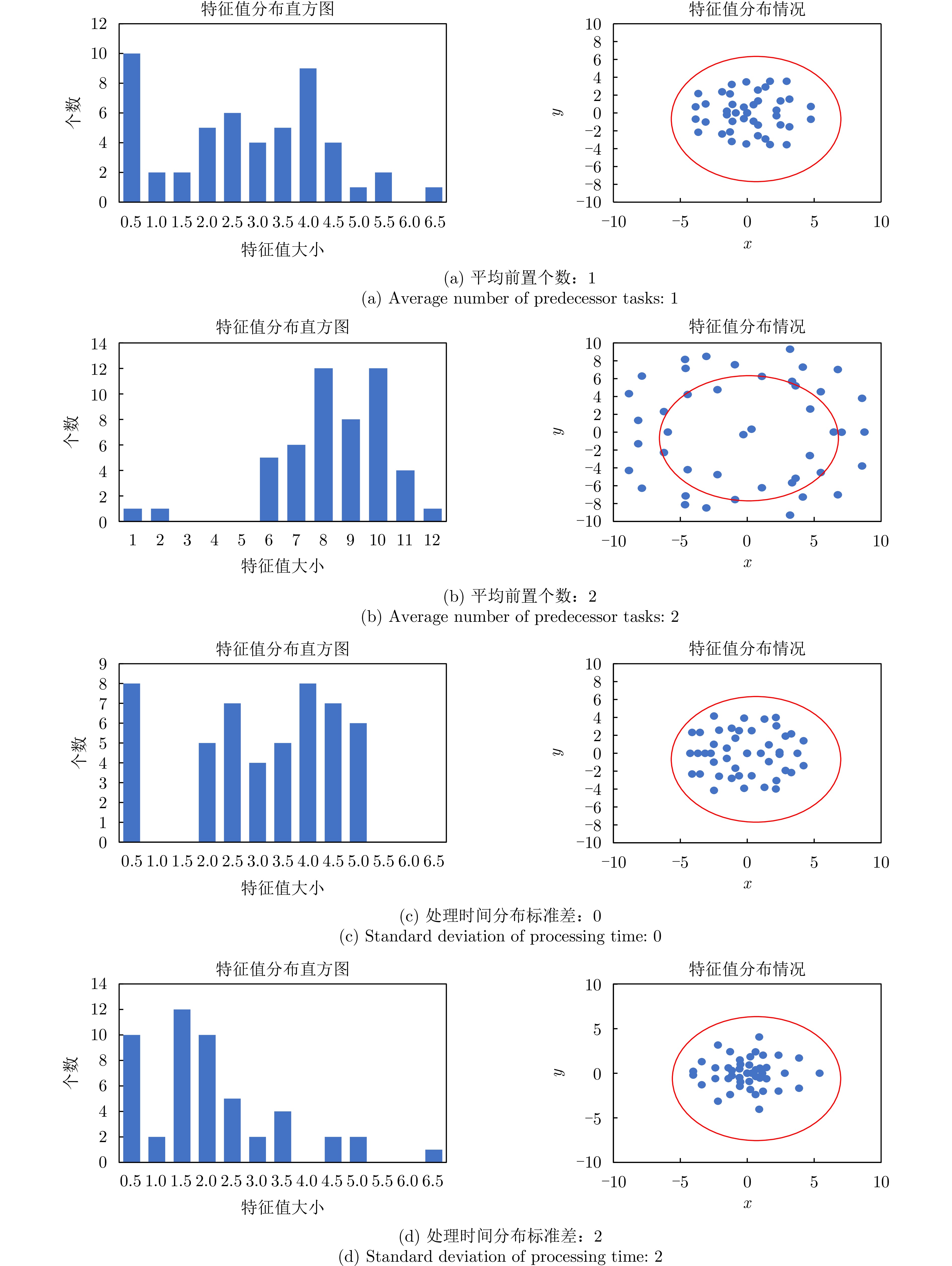
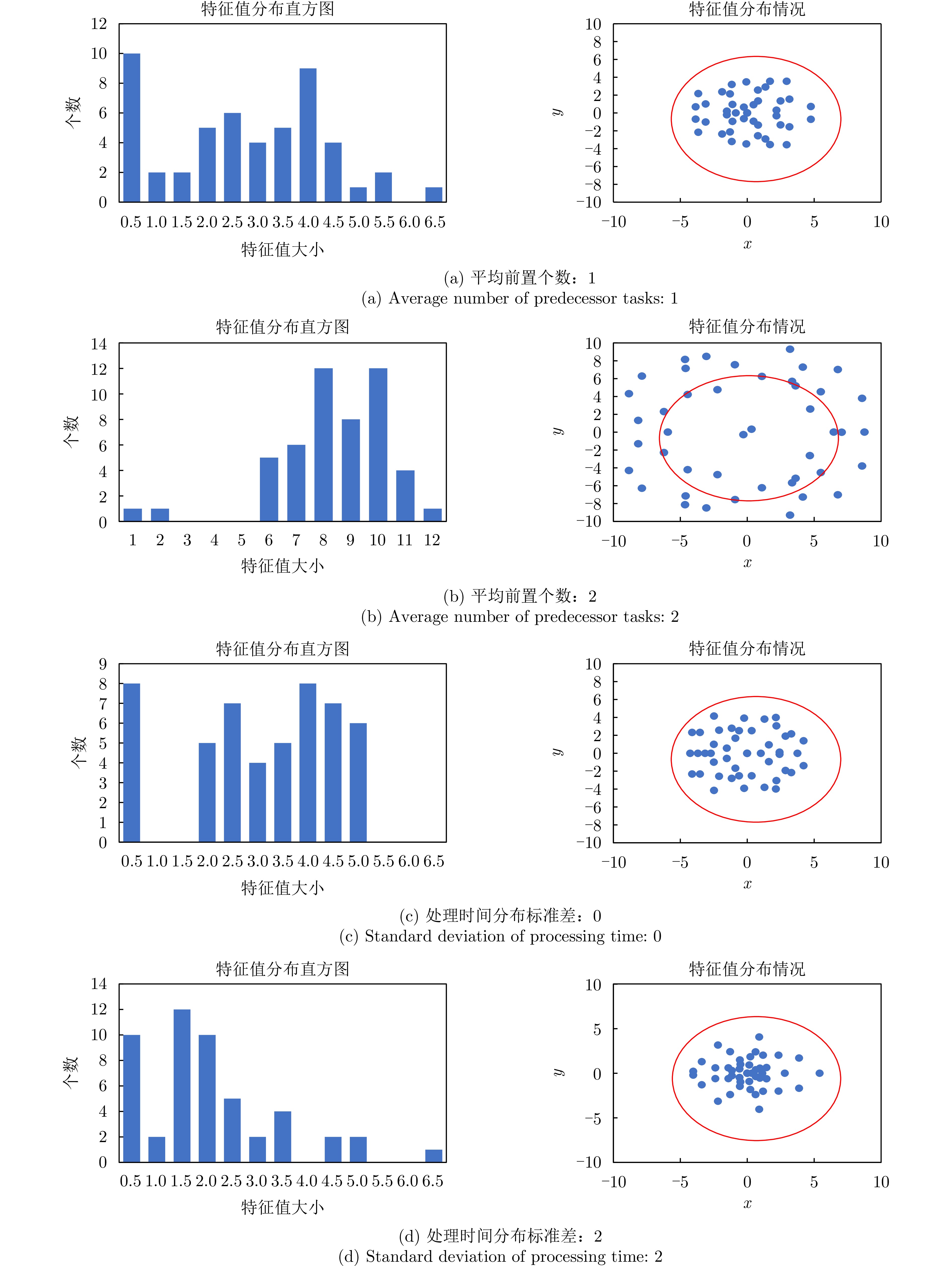
图6为不同参数下任务数据集的异构图表示经过随机变换后的谱分布情况，表2为对应的四维全局特征。图6(a)和图6(b)的区别在于前置逻辑约束个数不同，当平均前置任务个数增加时，特征在复平面上向外扩散分布，在直方图中大多数的特征值向右移动，特征值呈现增大和分散趋势。综合表2，平均前置任务个数增加，零特征值个数减少，说明问题异构图中的节点之间的连接关系变多，连通性增强；最小非零特征值减小，图可能更容易被分割成多个连通性较强的子图；特征值整体数值增大，因此谱半径和MSR显著变大。

图  6  不同参数任务数据集随机变换后的特征分布

Figure  6.  Distribution of features after random transformation of datasets with different parameter tasks

下载: 全尺寸图片 幻灯片

表  2  不同参数任务数据集的全局特征

Table  2.  Global characteristics of the dataset for different parameter tasks

参数	零特征值个数	最小非零特征值	谱半径	MSR
平均前置个数：1	9	0.7903	5.4809	2.3955
平均前置个数：2	0	0.0441	13.0964	7.9675
处理时间分布标准差：0	6	0.2592	4.9889	2.8304
处理时间分布标准差：2	6	0.5715	6.0868	1.9645

下载: 导出CSV 

| 显示表格

图6(c)和图6(d)的区别在于处理时间分布情况不同。处理时间作为权重矩阵$ {{\boldsymbol{W}}} $中存在连接的各项之间的权重值，其分布的标准差增加，则会导致拉普拉斯矩阵内各项的值分布差异增大，对应的特征值之间的差异也会增大，分布呈现密集、不均匀的特点。当处理时间分布标准差增加时，特征在复平面上的整体分布区域大致相同，但是有更多的特征向内聚集，在较小的范围内分布更为紧密；在直方图中大多数的特征值向左移动，特征值呈现减小和聚集趋势，MSR的值减小，谱半径数值增大。

3.3   基础图神经网络实现

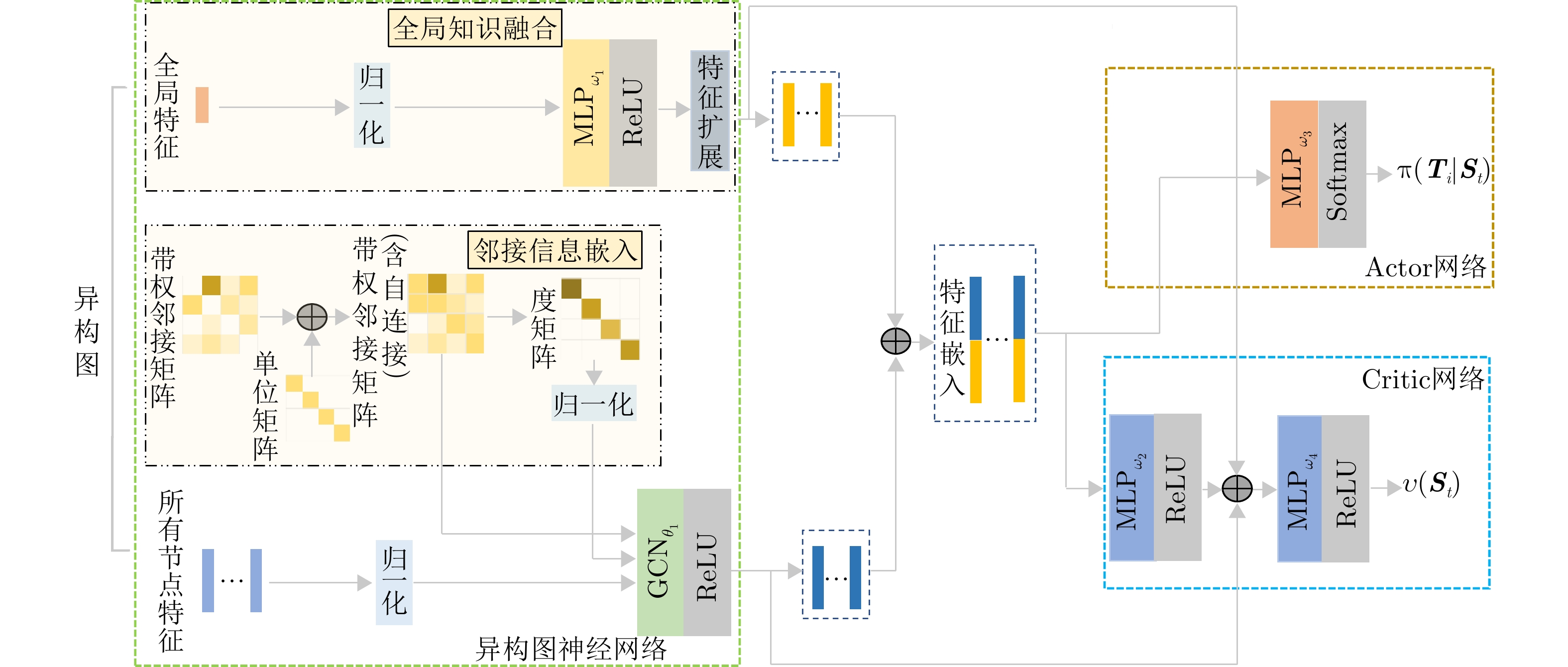
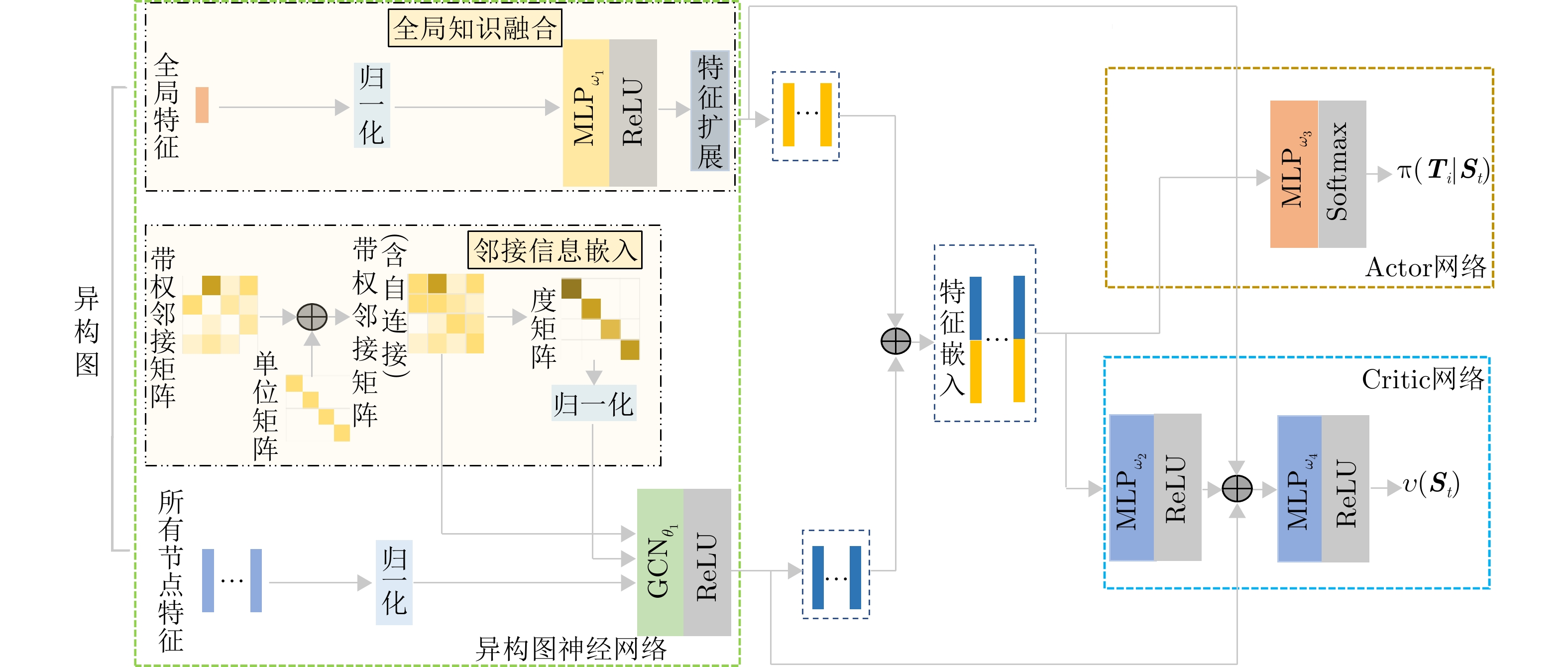
参考文献[40]，本文构建了由图卷积网络和多层感知机相结合构成的图神经网络对节点特征和全局特征进行提取和计算，以实现对图信息的有效编码。网络的结构如图7所示。

图  7  图神经网络结构图

Figure  7.  Graph neural network structure

下载: 全尺寸图片 幻灯片

本文使用的网络结构分为两部分：考虑异构图的邻接矩阵特性，使用图卷积神经网络对任务节点特征进行提取和嵌入；由于全局特征对于所有节点而言具有一致性，因此全局特征处理网络采用的是MLP结构。通过上述两步操作，把不同规模大小的调度问题用固定维度的特征信息嵌入，从而可以对不同规模的问题用同一套模型进行求解，提升了模型的通用性和适用性。

在网络训练过程中，对同一实例进行多轮训练过程，在任务决策过程中，将之前轮次训练得到的调度问题的最优可行解的目标值作为上界信息$ {{\varphi}}_{\rm{UB}} $，该解作为经验解，是问题调度成效的基准。假设当前所有可选任务集为$ {{{\boldsymbol{X}}}}_{{t}} $，对于任意任务$ {{a}}_{{t}}{\in}{\boldsymbol{X}}_{{t}} $，如果在当下时刻选择任务$ {{a}}_{{t}} $作为下一步调度的任务，任务$ {{a}}_{{t}} $的调度结果是可以确定的。根据前述数学模型，松弛约束(2)、约束(4)后，将问题看作独立的带时间窗的单雷达任务调度问题。对于在单处理器上调度一组不抢占的周期性或偶发任务的问题，EDF (Earliest Duel Time First)算法具有良好的性能。文献[9,41,42]中证明在非抢占式单机调度问题上，不考虑空闲时间任务插入情况，EDF方法是一种最优调度方法，因此在松弛关系约束的条件下，EDF的结果可以近似看成是原问题在取$ {{\phi}}_{{i}}{=1} $时的下界。

对于每个雷达$ {m} $，$ {\boldsymbol{T}}_{{m}} $表示雷达$ {m} $上的所有任务，按照任务截止期先后进行排序，对于截止期相同的任务，再根据优先级进行排序，得到任务的开始时间$ {\bar{{x}}}_{{i}} $。如果$ {\bar{{x}}}_{{i}}{\ge}{{d}}_{{i}} $，则任务执行成功；否则任务执行失败，进而计算出单个雷达调度的加权惩罚值$ {{\varphi}}_{{m}} $。

综合任务场景下的所有雷达得到调度问题的总加权惩罚值，由于任务的两条约束被松弛了，因此得到的结果是调度问题调度结果加权惩罚值的一个下界$ {{{{\varphi}}}}_{\rm{LB}}{(}{{a}}_{{t}}{|}{\boldsymbol{X}}_{{t}}{)} $。

如果$ {{\varphi}}_{\rm{LB}}\left({{a}}_{{t}}|{{{\boldsymbol{X}}}}_{{t}}\right){ > }{{\varphi}}_{\rm{UB}} $，说明当前状态下选择任务$ {{a}}_{{t}} $并不能带来比之前的决策更好的调度效果，应该降低选择任务$ {{a}}_{{t}} $的概率。反之，说明选择任务$ {{a}}_{{t}} $可能能够带来更好的调度效果。该方法得到的解作为网络学习过程中的引导解，将其与经验解结合可以辅助减小决策解的空间，指导算法的搜索方向和策略调整，提高算法的收敛速度和求解精度，提升调度效果。

4.   实验结果

4.1   性能评价指标

实验使用了以下几种评估指标来衡量模型的性能：

(1) 任务调度成功率：

(2) 相对调度评分RSS (Relative Schedule Score)。当使用多种方法进行结果对比时，根据调度成功率对每种方法进行打分，该分数用于衡量其他方法得到的成功率与目标方法得到的调度成功率的相对差距。对于目标方法m：

其中，$ \eta \left(m\right) $表示目标方法m的调度成功率，$ {{\boldsymbol{\eta}} }^{\rm{all}} $表示所有调度方法的调度成功率集合，$ {{\boldsymbol{\eta}} }^{\rm{other}} $表示除了目标方法m之外的其他所有调度方法的调度成功率集合。

(3) 加权调度成功率WSR (Weighted Success Rate)。考虑任务优先级计算加权调度成功率：

其中，$ {{\phi}}_{{i}} $表示当任务$ {i} $调度失败时导致的惩罚值，$ {{\phi}}_{{i}} $的大小与任务优先级相关，优先级越大，$ {{\phi}}_{{i}} $的值越大。

4.2   实验结果对比

4.2.1   神经网络模型训练数据生成

本文实验采用模拟生成的数据集。考虑了4类问题大小，模拟数据参数如表3所示。

表  3  任务实例生成

Table  3.  Task instance generation

大小	优先级	处理时间	截止期	前置任务个数	同步任务个数
10×3	U(1, 5)	U(1, 5)	U(8, 30)	U(0, 3)	U(0, 2)
20×3	U(1, 5)	U(1, 5)	U(8, 30)	U(0, 3)	U(0, 2)
20×10	U(1, 5)	U(1, 5)	U(12, 40)	U(0, 3)	U(0, 2)
30×5	U(1, 5)	U(1, 5)	U(12, 40)	U(0, 3)	U(0, 2)
注：U(a, b)表示在区间[a, b]上的随机分布。

下载: 导出CSV 

| 显示表格

4.2.2   模型知识融合的GNN训练模型性能

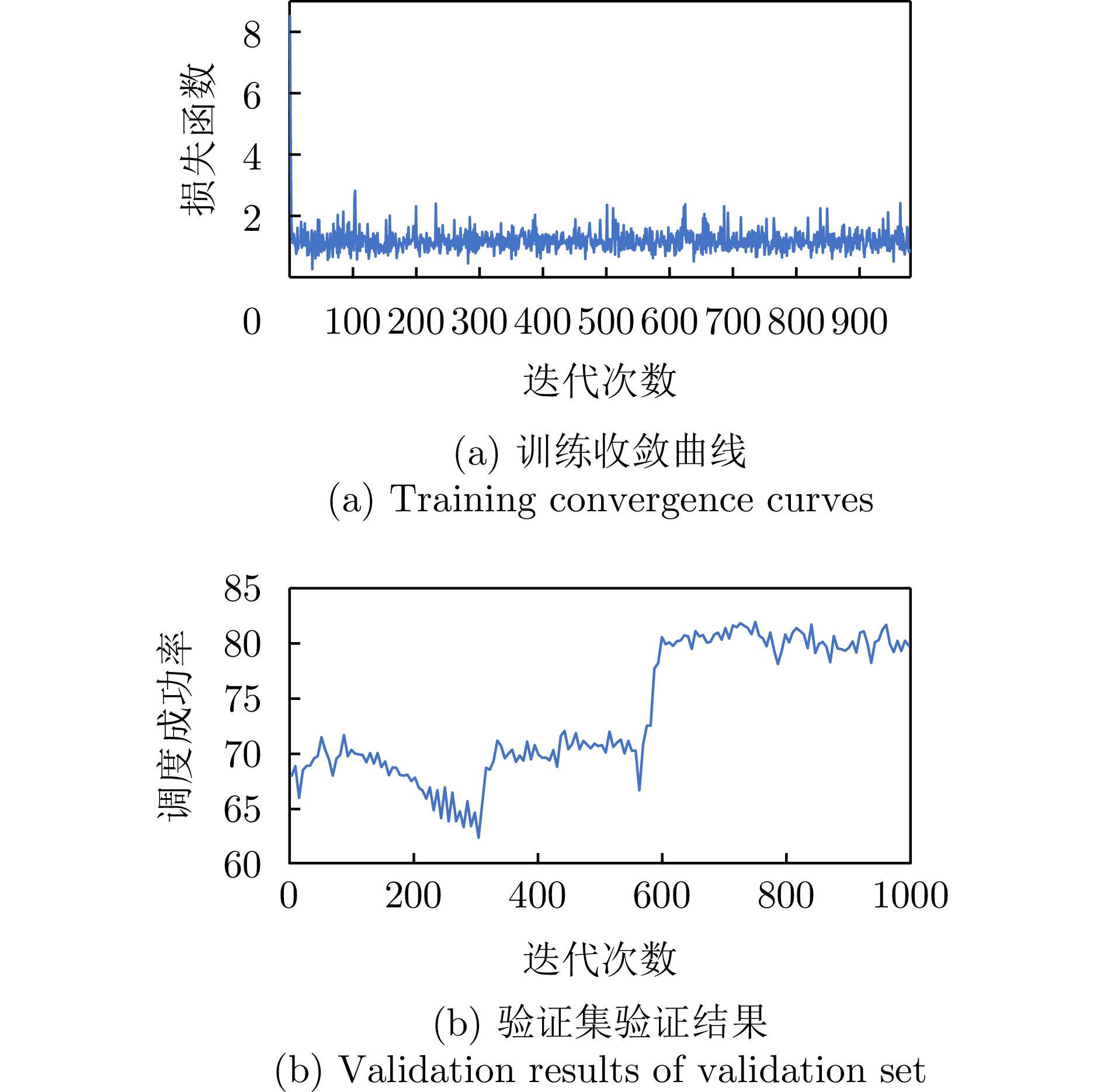
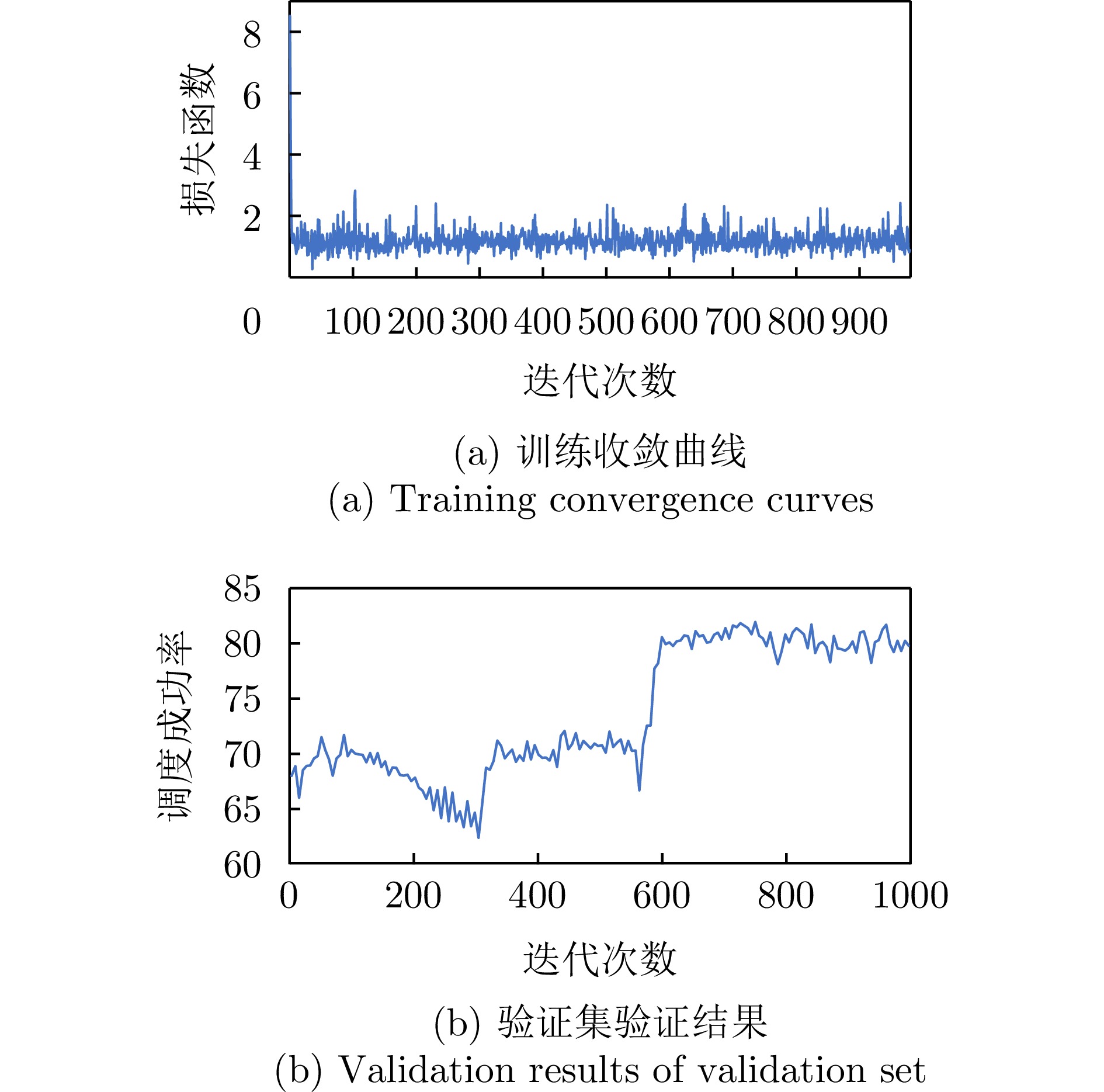
本文所提出的强化学习方法的训练过程相当稳定，并且收敛于所有4种训练规模。10×3上的训练曲线如图8所示，可以看出，在没有人为干预的情况下，强化学习确实可以基于自身的求解经验，从零开始学习高质量的调度策略。对不同规模训练集训练出的模型在相同的测试数据集上进行测试，结果见表4。对比可知，在10×3训练集上训练出的模型在其他规模大小的测试集上表现出的结果更好，本文之后的实验结果均基于此模型。

图  8  10×3实例上的训练曲线

Figure  8.  Training curves on instance 10×3

下载: 全尺寸图片 幻灯片

表  4  不同规模数据训练模型的测试结果(成功率)(%)

Table  4.  Test results (success rate) of models trained with datasets of different sizes (%)

测试集规模	10×3	20×3	20×10	30×5
10×3训练模型	96.10	83.35	97.90	84.40
20×3训练模型	94.60	80.50	96.75	80.63
20×10训练模型	95.10	80.50	96.95	80.57
30×5训练模型	93.40	80.30	96.45	81.03

下载: 导出CSV 

| 显示表格

4.2.3   数据仿真对比

本实验关注的对比方法主要有：规则调度：先进先出(First In First Out, FIFO)，最长处理时间(Largest Process Time, LPT)，最早截止期(Earliest Duel Time First, EDF)等；综合加权打分规则调度(Score)：根据任务的优先级大小，截止期，处理时长和任务唯一标识对任务进行打分，调整各项分数的权重得到综合评分结果；不考虑全局特征的强化学习方法(GNN)：不考虑全局特征，采用与本文相同的网络结构和训练方法得到的深度强化学习模型；基于分支定界法的调度策略(BBM)^[13]；基于广义时间窗的调度策略(GTW)^[21]。

参考文献[13,14]，根据类型和优先级将任务分为6类，设置测试用例如表5。定义前置约束：低优先级搜索→高优先级搜索任务，高优先级搜索→精度跟踪，各三对。定义高精度跟踪和精度跟踪任务中共有4个任务需要两台雷达协同执行。实验所用平台为：CPU: i5-9400F, 2.90GHz; GPU: NVIDIA GeForce GTX 1660 SUPER；操作系统：64位Win11；Python3.8版本；pytorch1.10.0+cu102。记录对比试验结果如表6所示。文章所提出的方法在调度成功率和加权调度成功率方面表现较好，平均任务调度耗时相较GNN方法长，这是因为我们进行了全局特征提取以及问题上下界计算过程。综合打分方法的计算耗时最少，其方法的复杂度最低，但是调度效果不够显著。

表  5  任务参数

Table  5.  Task parameters

类别	类型	数量	驻留时长	截止期
跟踪确认TC	6	10	9	250
高精度跟踪HPT	5	10	8	250
精度跟踪PT	4	15	6	100
普通跟踪NT	3	15	4	100
高优先级搜索HS	2	20	2	100
低优先级搜索LS	1	20	1	100

下载: 导出CSV 

| 显示表格

表  6  结果对比

Table  6.  Comparison of results

方法	成功率(%)	加权成功率(%)	平均任务调度耗时(s)
MKEGNN	86.17	85.67	0.773
GNN	81.91	82.98	0.703
BBM	79.79	79.18	0.726
GTW	75.53	80.89	0.570
Score	76.60	78.16	0.012
注：平均任务调度耗时=计算耗时/调度成功任务个数。

下载: 导出CSV 

| 显示表格

为了探究算法对不同类型问题的调度效果，本实验也生成了不同类型的模拟仿真测试数据集，实验考虑两类不同场景，一类为不同的任务和雷达数目，即为不同实例规模，另一类为不同的前置任务数量，即为不同的逻辑约束复杂程度。具体的参数设置见表7。

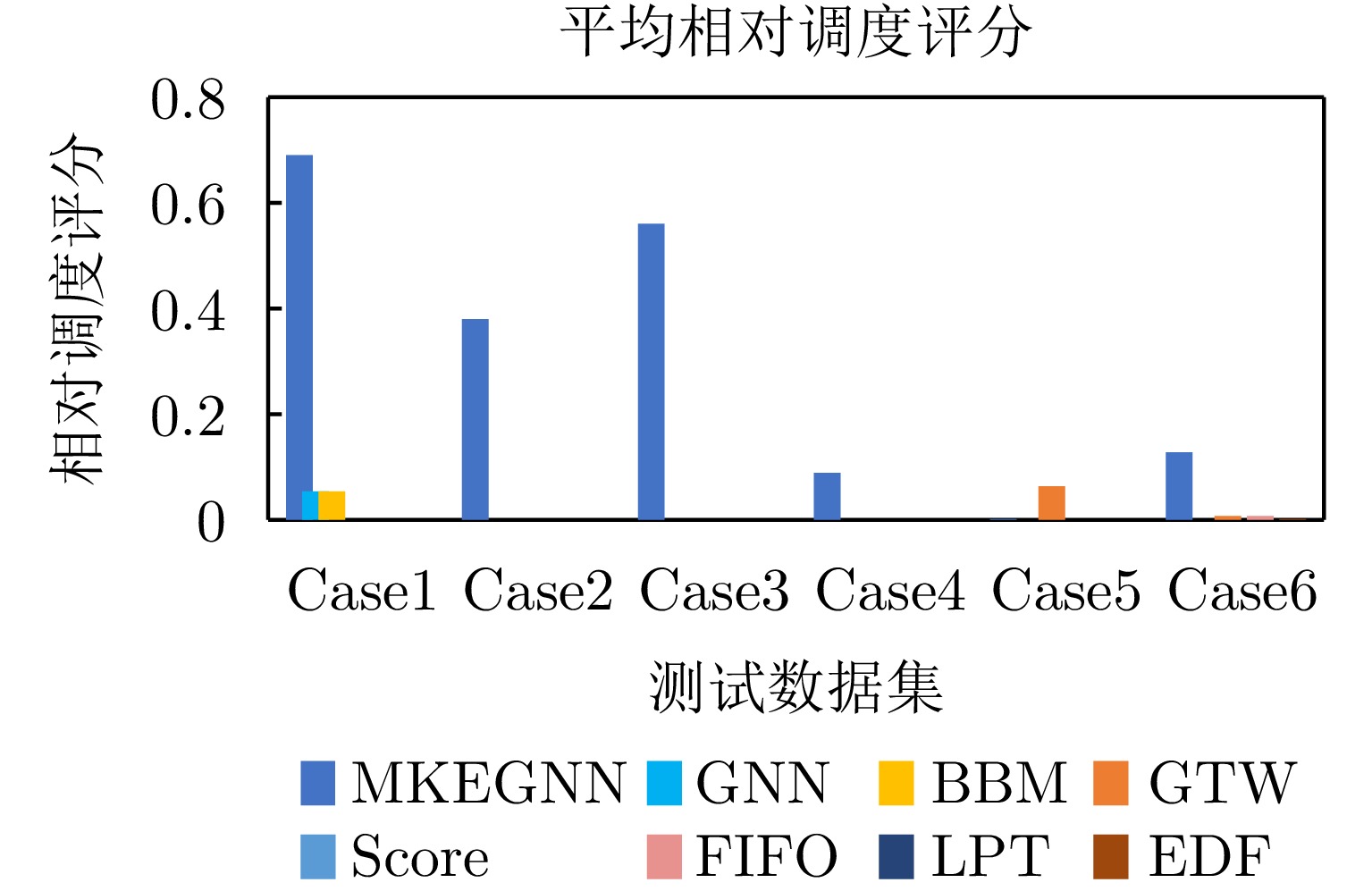
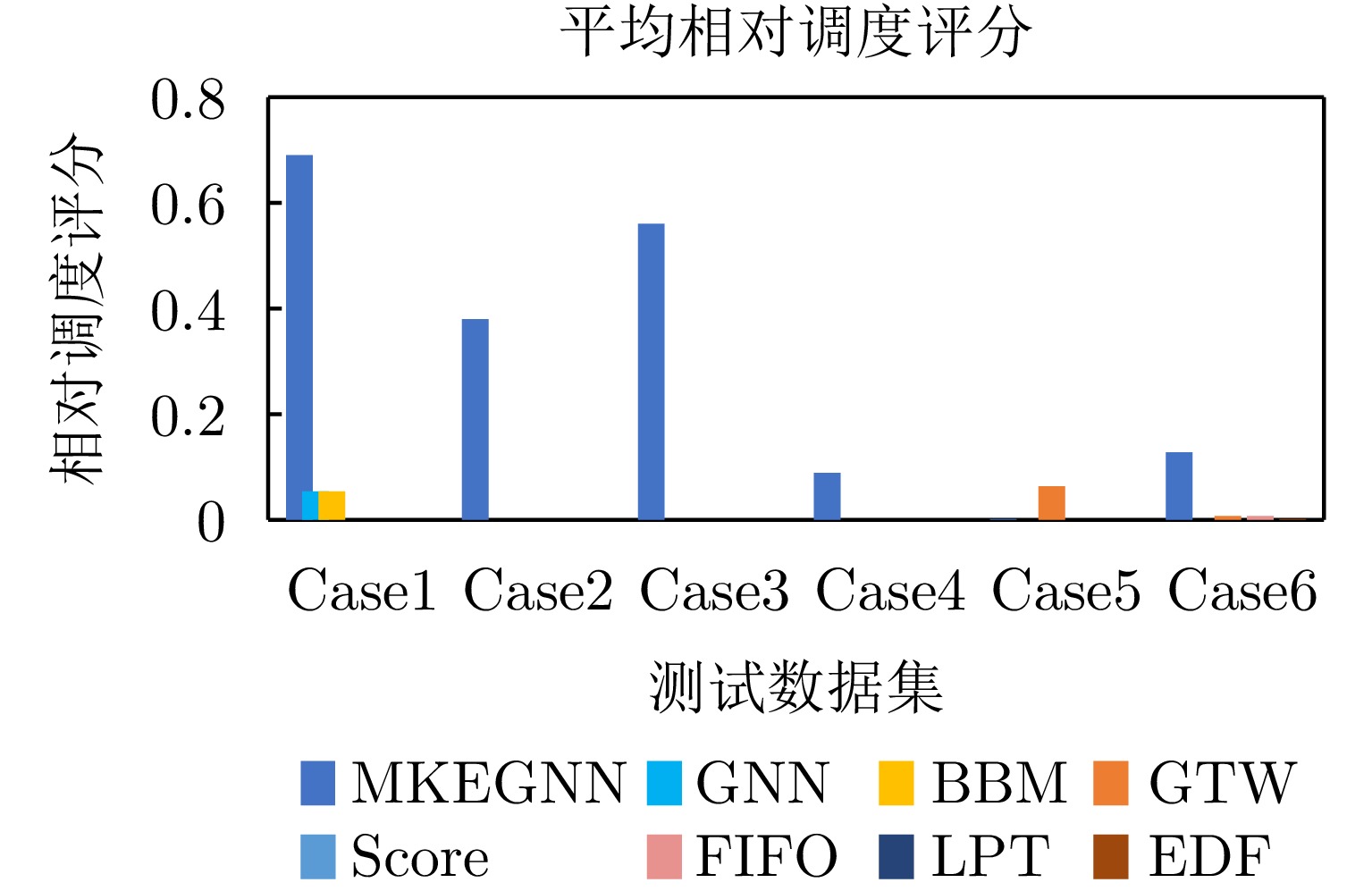
表  7  测试集实例生成

Table  7.  Test instance generation

实例	任务数	雷达数	优先级	处理时间	截止期	前置任务个数	同步任务个数
Case1	20	3	U(1, 5)	U(1, 5)	U(8, 30)	U(0, 1)	U(0, 2)
Case2	20	3	U(1, 5)	U(1, 5)	U(8, 30)	U(0, 3)	U(0, 2)
Case3	30	5	U(1, 5)	U(1, 5)	U(12, 40)	U(0, 1)	U(0, 2)
Case4	30	5	U(1, 5)	U(1, 5)	U(12, 40)	U(0, 3)	U(0, 2)
Case5	60	5	U(1, 5)	U(1, 5)	U(16, 60)	U(0, 1)	U(0, 2)
Case6	60	5	U(1, 5)	U(1, 5)	U(16, 60)	U(0, 3)	U(0, 2)
注：U(a, b)表示在区间[a, b]上的随机分布。

下载: 导出CSV 

| 显示表格

实验对6类case各取10个实例进行调度，记录不同算法在这10个实例上的平均调度成功率如表8所示。当资源无法实现对所有任务的有效调度时，调度结果显示本文提出的算法调度成功率明显优于其他7种算法。且不论是在规模大小不同的场景还是在任务关联度高低不同的场景下，本文算法的调度成功率都比GNN算法高，说明基于全局知识融合的方法找到了较好的全局特征表达，问题共性特征刻画准确。通过对比3种规则调度方法在不同类型实例上的表现也证明了，规则调度有其适用的特定场景，通用性较弱。实验也记录了不同算法在这些实例上的加权调度成功率，见表9。结果表明，MKEGNN方法的加权调度成功率指标比其他方法更优秀，这说明MKEGNN方法在调度时，具备对于任务的优先级特性的学习能力，所给出的策略质量更优秀。实验也对7种方法进行相对调度评分计算，如图9所示，本文所提出的算法的打分基本高于其他7种，算法总体性能相对其他算法提升3%～10%，具有显著优势。

表  8  任务调度成功率(%)

Table  8.  Success ratio of scheduling (%)

实例	MKEGNN	GNN	BBM	GTW	Score	FIFO	LPT	EDF
Case1	80.5	70.5	72.5	67.0	65.5	63.0	59.5	71.0
Case2	58.5	53.0	52.5	48.0	48.5	48.5	42.5	50.5
Case3	90.3	81.6	78.6	79.0	77.6	72.3	70.7	81.0
Case4	52.0	49.7	45.7	52.0	48.0	45.3	47.3	46.0
Case5	85.7	85.6	70.2	80.2	72.7	66.5	63.3	77.8
Case6	45.0	44.2	40.8	42.0	40.0	39.4	39.5	40.8

下载: 导出CSV 

| 显示表格

表  9  任务加权调度成功率(%)

Table  9.  Weighted success ratio of scheduling (%)

实例	MKEGNN	GNN	BBM	GTW	Score	FIFO	LPT	EDF
Case1	81.9	69.9	71.2	68.5	63.9	61.1	58.2	70.8
Case2	61.3	54.7	55.2	50.4	50.9	50.7	44.9	53.0
Case3	90.8	80.9	79.4	80.0	78.4	72.6	70.6	81.0
Case4	52.7	50.1	44.8	52.5	47.8	44.4	47.1	46.0
Case5	86.2	81.0	70.0	82.2	74.0	65.5	63.7	78.1
Case6	46.6	44.0	42.5	43.8	41.0	41.2	41.1	42.9

下载: 导出CSV 

| 显示表格

图  9  平均相对调度评分

Figure  9.  Average relative scheduling score

下载: 全尺寸图片 幻灯片

从case4中随机挑选一个测试实例进行调度，计算不同优先级任务的调度成功率如表10所示。总计5种任务优先级，MKEGNN方法在其中4种优先级任务上的调度成功率均取得最优，且在优先级为5的任务上调度成功率也较为优秀，说明算法保障了重要任务优先调度。

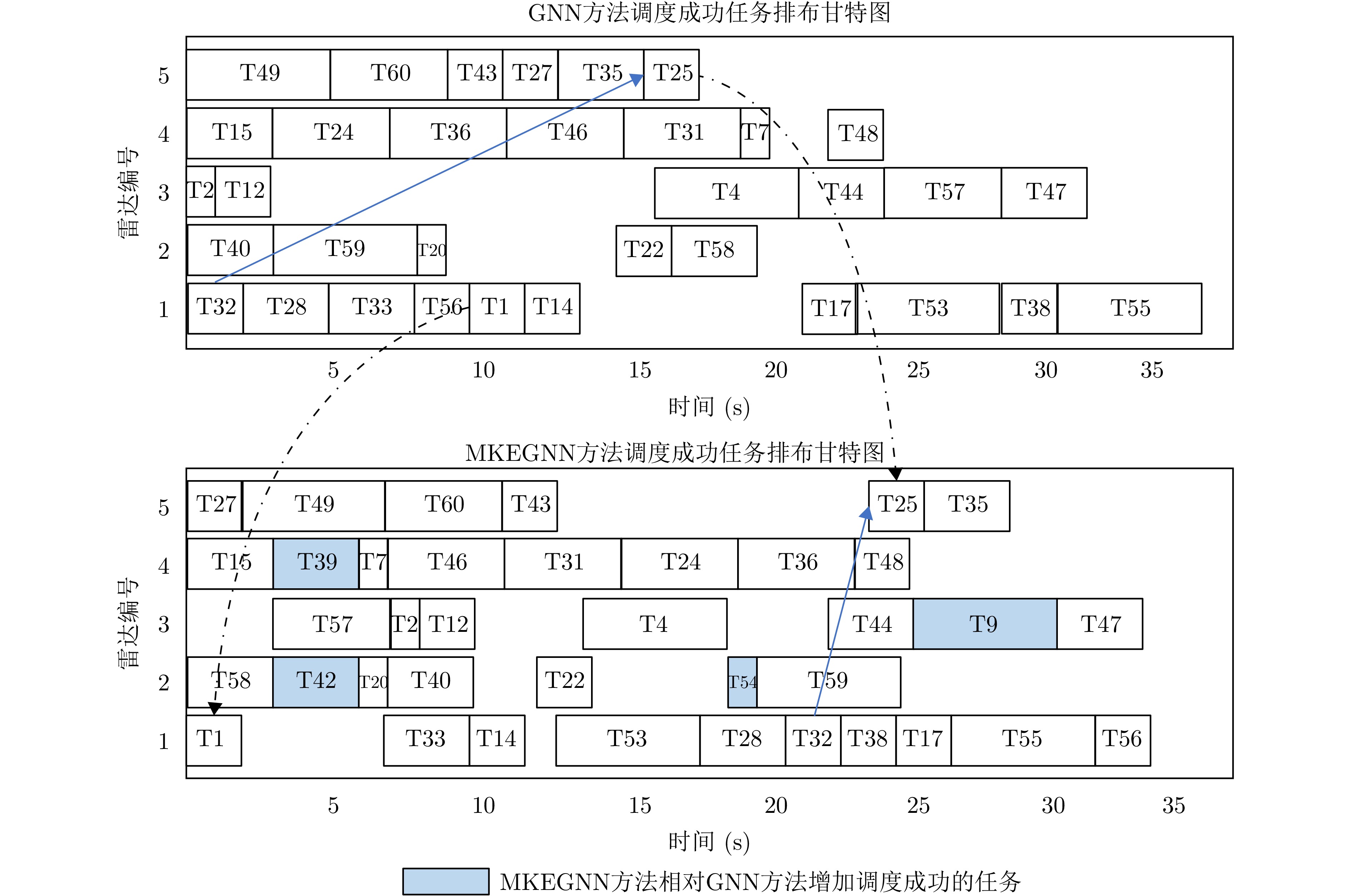
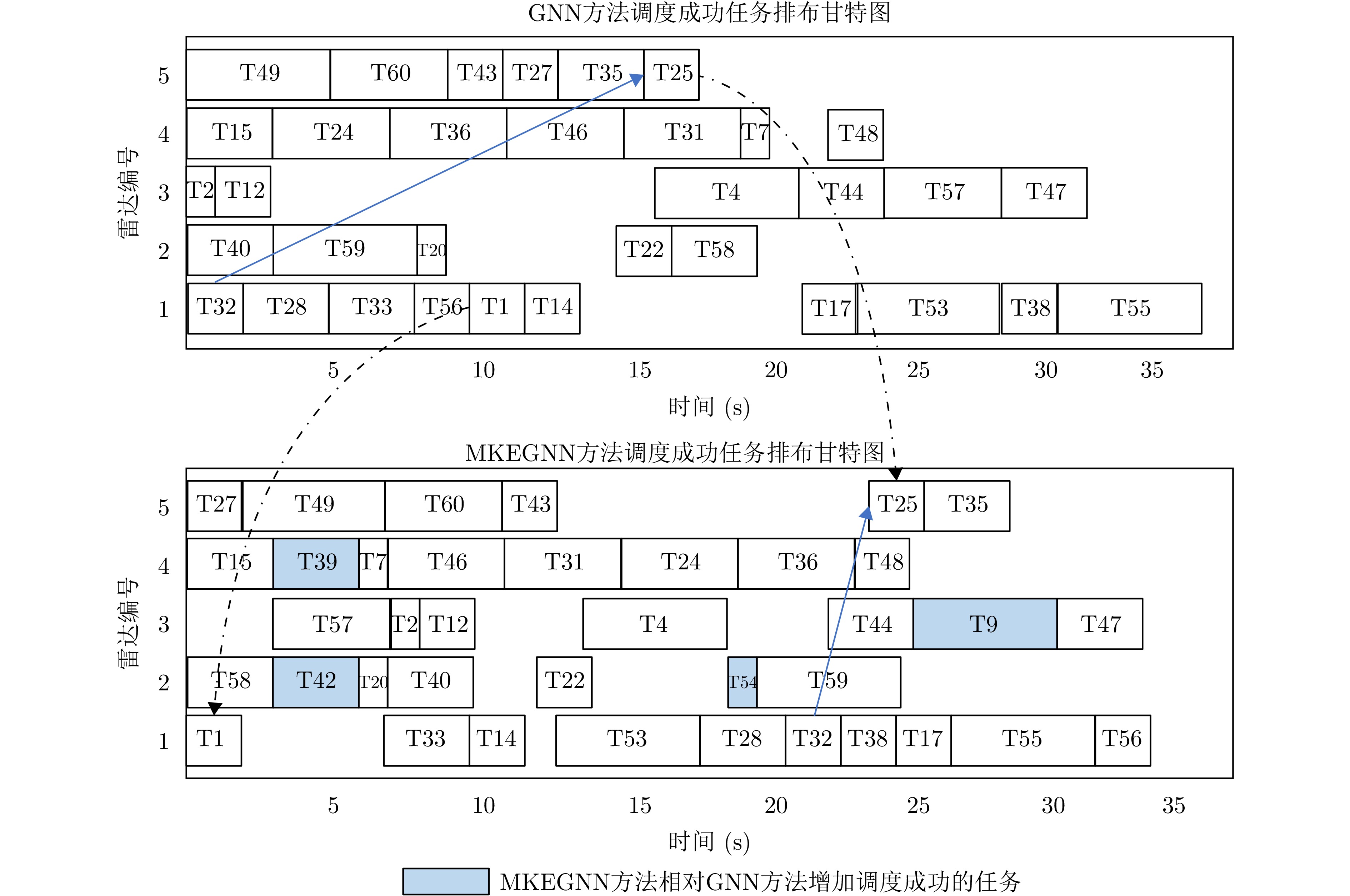
表  10  各优先级任务调度成功率(%)

Table  10.  Success ratio of scheduling of different priority (%)

优先级	MKEGNN	GNN	BBM	GTW	Score	FIFO	LPT	EDF
5	88.8	66.6	88.8	88.8	88.8	66.7	55.6	77.8
4	100	100	83.3	83.3	83.3	83.3	100	100
3	100	50.0	50.0	50.0	75.0	25.0	75.0	75.0
2	80.0	60.0	60.0	40.0	60.0	80.0	80.0	60.0
1	83.3	83.3	83.3	100	83.3	50.0	50.0	83.3

下载: 导出CSV 

| 显示表格

从case6中随机挑选一个测试实例进行调度，绘制调度成功任务甘特图对比图如图10所示，图10中标注出了部分调度结果不同的任务，在60个待调度任务中，GNN方法成功调度了34个，最后一个成功调度任务的完成时间为第37 s，而MKEGNN方法成功调度了38个任务，从图中可以看出，MKEGNN方法分别在第2, 3, 4号雷达上增加了调度成功的任务，调度成功率更高。对于任务25，由于其具有前置任务32，在MKEGNN方法的调度结果中将任务25排布在第23 s执行。MKEGNN方法所有调度成功任务的完成时间为34 s，在总体任务的执行时间更短的情况下，成功执行了更多的任务，调度效率有较大提升。

图  10  两种GNN模型对相同实例的成功调度结果甘特图对比

Figure  10.  Comparison of successfully scheduling results gantt charts of two models on the same instance

下载: 全尺寸图片 幻灯片

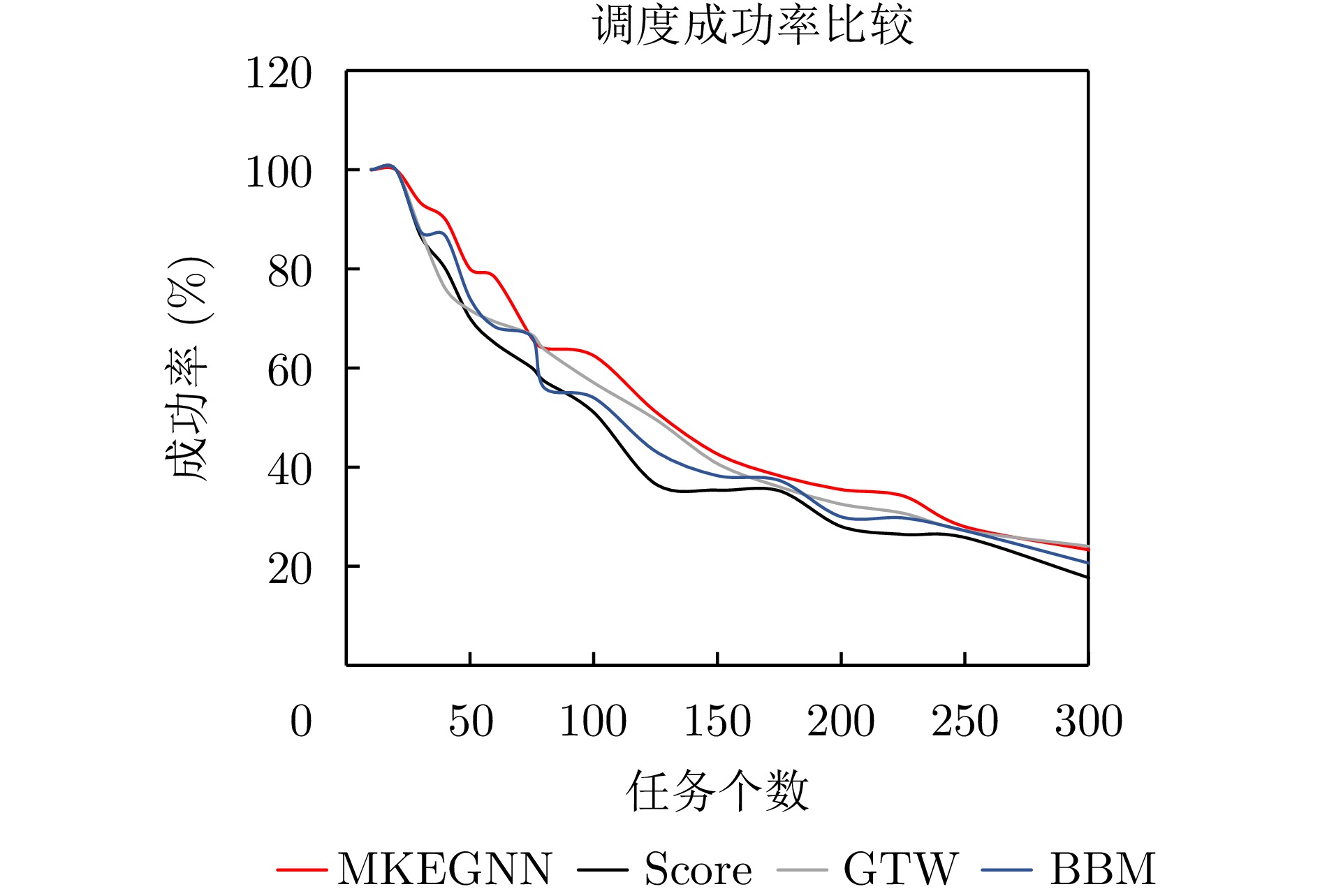
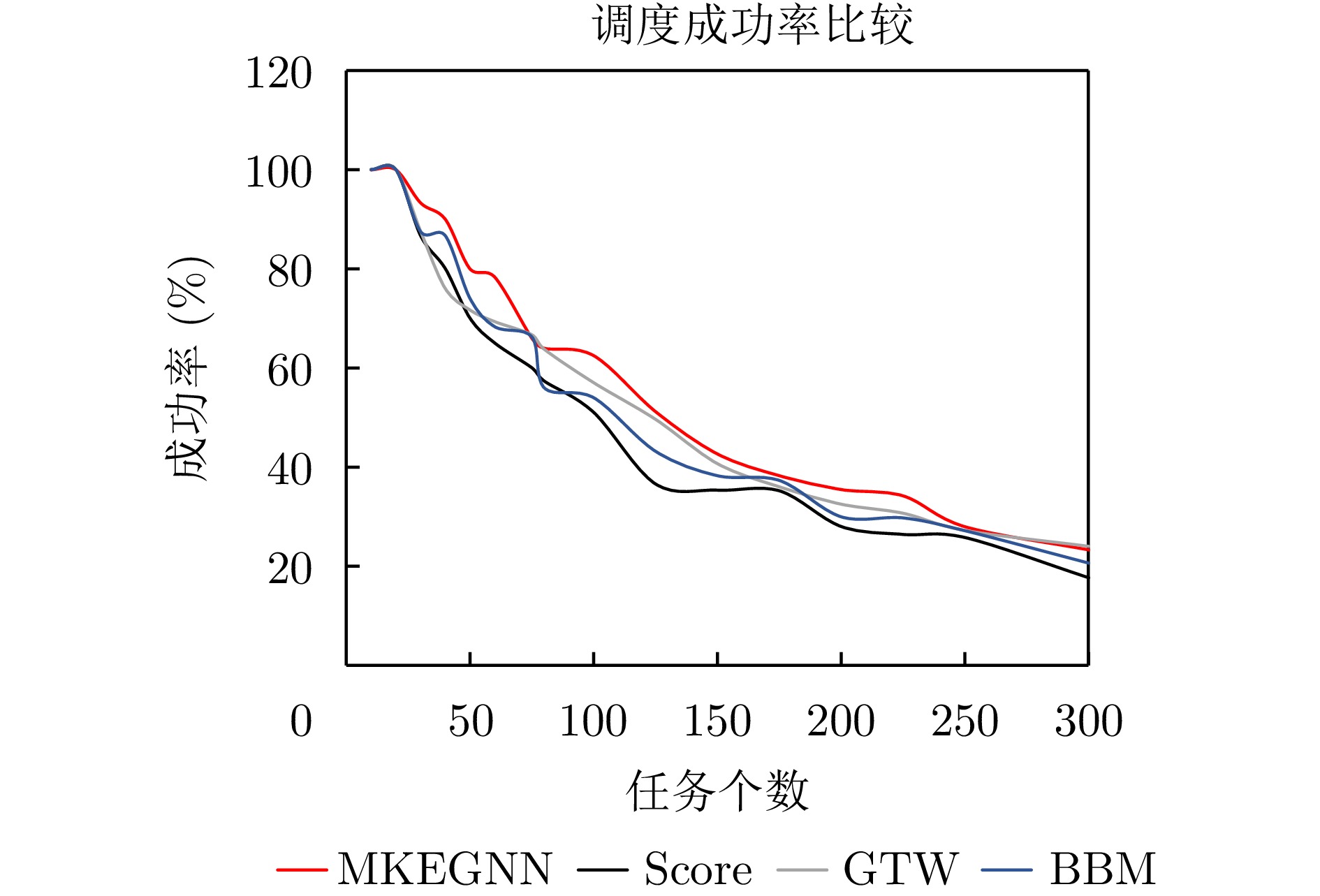
为验证任务规模对算法性能的影响，采用case3的生成参数，生成任务个数在10～300范围内的测试用例。调度成功率对比如图11，当任务个数较少时，雷达资源充裕，所有的算法都能实现任务的完全调度；随着参与调度的任务个数增多，4种算法的成功率均呈下降趋势，当任务个数达到250个以上时，4种算法的成功率下降到了相似的水平，这是因为雷达资源接近饱和导致的。从总体的走势来看，文章所提出的方法在成功率方面比其他方法表现更优。

图  11  算法性能比较

Figure  11.  Algorithm performance comparison

下载: 全尺寸图片 幻灯片

4.2.4   模型鲁棒性检验

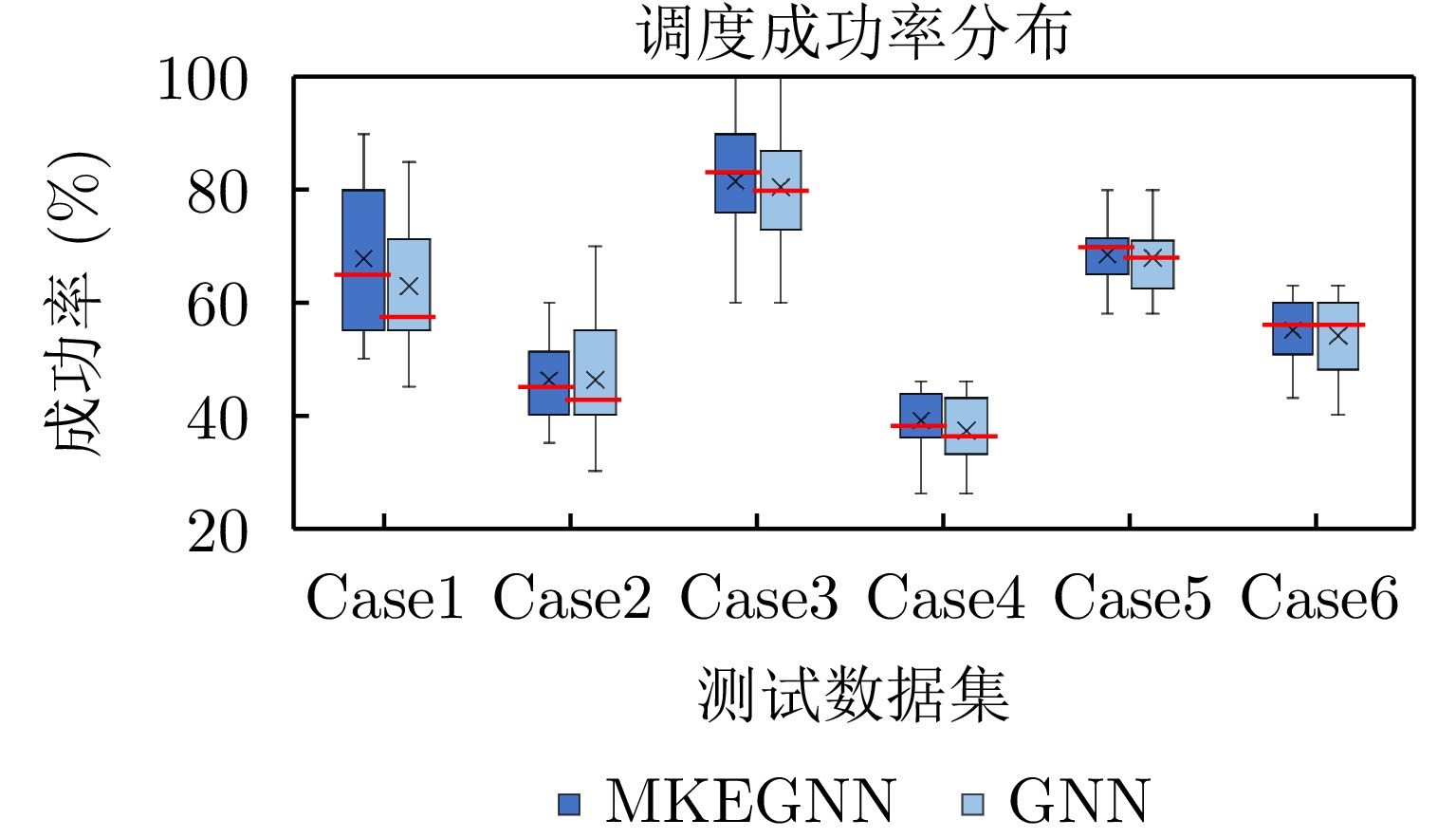
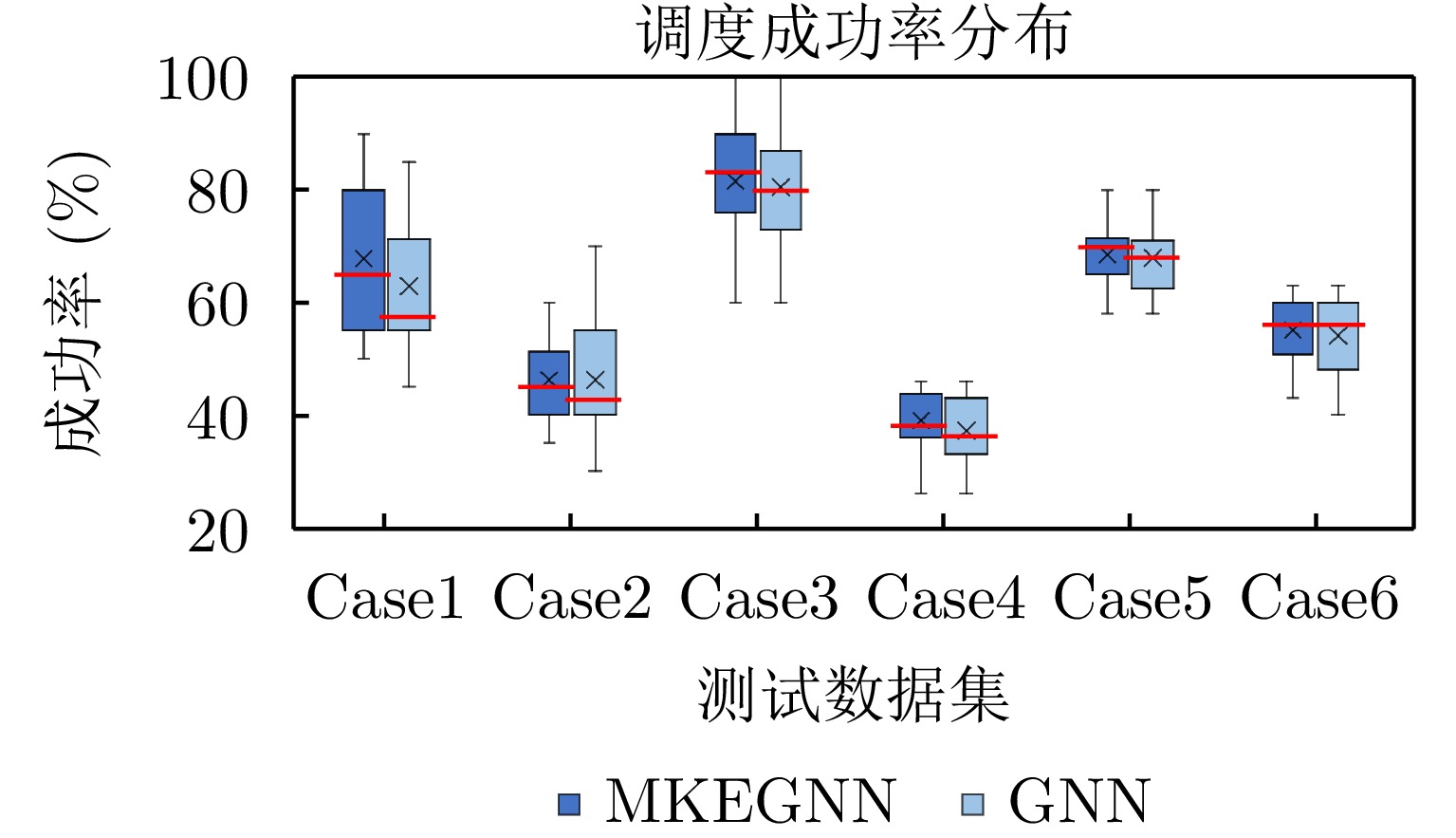
实验在4.2.3节所生成的6类数据集中各随机选择了一个实例进行了50次随机模拟实验，决策根据概率进行随机采样。本文提出的方法MKEGNN与GNN方法对比结果如图12所示。可以看出，在这两个问题上，MKEGNN调度成功率的中位数均大于GNN方法，且四分位距较小，说明成功率的离散程度低，稳定性较好，尤其是当任务数较多，截止期紧迫，并且前置任务和同步更为复杂时，优势更加明显。说明考虑了全局特征后，模型的稳定性和鲁棒性有了提升。

图  12  1个实例调度50次，两种模型的调度结果

Figure  12.  Scheduling results for both models on one instance

下载: 全尺寸图片 幻灯片

5.   结语

在本文的实验研究中，我们采用拉普拉斯矩阵来精确描述图的结构信息，并通过随机化处理和求解平均谱半径等先进技巧，深入揭示了任务间复杂的相互作用和依赖关系，以及系统中资源和任务之间的匹配程度。具体而言，较小的平均谱半径反映了工序时间分布和任务资源分配的均衡性，而较大的平均谱半径则暗示了资源利用的不均衡或负载过重的情况。这一全局特征为模型提供了有力的指导，使其能够更有效地进行调度和资源分配。该方法所提供的全新的全局视野，从问题的整体特点出发，关注共性特征，对于其他调度问题，例如柔性作业车间调度问题，雷达资源分配问题等均有适用性和泛化性。

本文所提出的调度模型，不仅全面考虑了图结构的全局信息，而且展现了在解决不同类型与规模问题时的有效性和适用性。此外，基于引导解和经验解来计算问题上下界的做法，在决策时可以预先筛选掉一部分低效解，提升了调度结果成功率。值得注意的是，雷达任务调度问题是一个典型的多目标、多约束、动态变化的复杂优化问题。其动态变化的特性要求调度算法必须具备高度的灵活性和适应性，以应对任务情况的实时变动。因此，在未来的研究中，我们将持续关注并改进调度算法，以更好地适应这种动态变化的环境。