-
摘要: 随着电磁频谱成为现代战争的关键作战域之一,在未来军事作战中,现代雷达将面临日益复杂、灵巧和智能的电磁干扰环境。认知智能雷达具备环境主动感知、任意发射和接收设计、智能处理和资源调度等能力,可适应复杂多变的战场电磁对抗环境,是雷达技术领域重点发展的方向之一。该文将认知智能雷达从结构上分解为认知发射、认知接收、智能处理以及智能控制等4大功能模块,梳理出干扰感知、发射设计、接收设计、信号处理和资源调度等认知智能雷达每个环节的抗干扰原理,并对近几年代表性文献进行归纳总结,分析了该领域技术发展趋势,旨在为以后的技术研究提供必要的参考和依据。Abstract: As the electromagnetic spectrum becomes a key operational domain in modern warfare, radars will face a more complex, dexterous, and smarter electromagnetic interference environment in future military operations. Cognitive Intelligent Radar (CIR) has become one of the key development directions in the field of radar technology because it has the capabilities of active environmental perception, arbitrary transmit and receive design, intelligent signal processing, and resource scheduling, therefore, can adapt to the complex and changeable battlefield electromagnetic confrontation environment. In this study, the CIR is decomposed into four functional modules: cognitive transmitting, cognitive receiving, intelligent signal processing, and intelligent resource scheduling. Then, the antijamming principle of each link (i.e., interference perception, transmit design, receive design, signal processing, and resource scheduling) of CIR is elucidated. Finally, we summarize the representative literature in recent years and analyze the technological development trend in this field to provide the necessary reference and basis for future technological research.
-
1. 引言
随着电磁频谱成为现代战争的关键作战域之一,战场电磁频谱优势的争夺已成为决定战争胜败的关键技术手段之一。因此,在未来军事对抗中,现代雷达将面临日益复杂、灵巧和智能的电磁干扰环境。特别是随着数字化技术、射频电子技术和智能化技术的快速发展,现代数字射频存储(Digital Radio Frequency Memory, DRFM)认知干扰机通过对雷达信号进行截获、存储、调制与转发,产生与真实目标回波高度相似的假目标干扰,对雷达实现“饱和式”攻击,极大降低了雷达的探测性能。
2006年,加拿大Haykin[1]首次提出了具备闭环发射、接收和处理架构的认知雷达概念。与传统雷达不同,认知雷达能够根据外界环境变化,可以自适应地调整发射波形和接收处理方法,具备了适应更加复杂战场电磁环境的能力。近年来,随着认知雷达技术和人工智能技术的不断发展,从功能上,雷达逐渐具备认知能力和智能进化能力,从而形成一种新的雷达体制——认知智能雷达。
认知智能雷达具有闭环学习自进化的雷达架构,具备环境自适应感知、任意发射和接收设计、智能处理和资源调度等能力,可以适应复杂多变的电磁对抗环境。从功能结构上,认知智能雷达主要由认知发射、认知接收、智能处理以及智能调度4大功能模块组成,如图1所示。
认知发射:主要是利用雷达目标与电子干扰的先验知识、雷达回波历史数据以及战场环境实时认知信息,在雷达发射端,认知最优化设计发射波形、发射波束以及发射功率等,在复杂的电磁对抗环境中,提升反侦察和抗干扰能力。从雷达与干扰的博弈过程可以看出,雷达相对于干扰的优势主要体现在掌握了发射主动权,而干扰只能被动跟随雷达的变化而改变。认知发射是认知智能雷达的核心之一,其实质是充分利用发射主动权,通过捷变、随机、诱骗和协同等多种发射策略,提升雷达在复杂电磁环境的适应和生存能力。
认知接收:在雷达接收端进行认知最优化设计,实现接收回波信号在空域、时域、频域和极化域等上的滤波。其核心是尽可能阻止干扰能量混叠在雷达目标回波上,为后续信号和数据处理提供相对干净的回波信号。根据具体应用需求,认知发射和认知接收可以进行一体化优化设计,例如:发射波形和接收滤波器联合设计[2],提升雷达系统抗干扰和反杂波能力。
智能处理:结合人工智能技术,对混叠有电子干扰、地海杂波和雷达目标回波的信号进行智能化处理,提取干扰杂波高维特征,进而消除干扰和地海杂波的影响,实现对雷达目标的智能检测、跟踪和识别。智能处理是认知智能雷达的关键,其实质是结合人工智能技术,利用深度神经网络分别替代传统的检测算法、跟踪算法和识别算法等,甚至可以实现检测-跟踪-识别一体化,挖掘掩藏在数据中人们难以直观理解的深度特征。
智能调度:借助先验知识与实时认知信息,对智能处理的结果进行效能评估、预测推理以及智能决策,并对雷达任务、对抗策略、系统资源和处理算法的智能多层级调度,实现雷达探测能力闭环自进化[3-6]。智能调度在认知智能雷达中起到中枢核心作用,类似于人的大脑,基于记忆和经验,对处理结果进行分析判断,并对电磁态势的未来变化进行智能预测,从而决定雷达下一个时间段执行的任务、发射的波形、使用的接收滤波器和处理算法等,实现有限资源约束下雷达整体探测效能最大化。
目前,国内外学者对认知智能雷达的抗干扰技术开展了大量研究,其中,干扰感知属于智能处理的重要环节,我们将其作为单独一节进行总结。为了更好地展现认知智能雷达的闭环工作流程,下面将从干扰感知、抗干扰发射、接收、处理和调度方面,对国内外的文献进行归纳分析,并总结出未来的技术发展趋势。
2. 认知智能雷达干扰感知技术
干扰感知主要实现对干扰特征的估计,为抗干扰决策提供信息支持。根据干扰特征维度,干扰特征可分为浅层特征与深层特征。浅层特征一般指有实际意义的物理特征,包括干扰频谱、多普勒以及脉内调制特征等;深层特征主要是指经过深层神经网络映射的高维特征空间中的语义特征,一般没有明确的物理含义。
2.1 干扰浅层特征估计技术
现有浅层特征估计主要通过概率统计、时频变换、高阶矩阵变换等技术,提取干扰信号的物理特征,实现干扰类型识别和参数估计。
2.1.1 基于浅层特征的干扰类型识别
基于浅层特征的干扰类型识别是利用概率统计、时频变换、高阶矩阵变换等技术,提取不同干扰在时域、频域、多普勒域等不同调制域的特征差异,实现对干扰类型的识别。
针对距离欺骗干扰,文献[7,8]分析了距离欺骗干扰信号的产生机理,揭示了DRFM技术缺陷会导致距离欺骗干扰信号在频域中心产生频率偏移等问题,为距离欺骗干扰识别提供参考。文献[9]建立了欺骗干扰的数学模型,提出了干扰双谱特征和支持向量机(Support Vector Machine, SVM)分类器联合的干扰类型识别方法。针对距离拖引干扰、速度拖引干扰和距离速度同步拖引干扰,文献[10]提出了一种基于小波分解的干扰类型识别方法,提取了归一化一维小波变换系数谱的能量比参数。文献[11]提出了一种基于时频变换的干扰类型识别方法,提取了时频域可分离度和3阶Renyi熵等干扰有效特征。然而上述方法仅能识别欺骗干扰。文献[12]提出了一种基于熵理论的干扰估计方法,可有效区分速度欺骗干扰与压制式干扰。
2.1.2 基于浅层特征的干扰参数估计
基于浅层特征的干扰参数估计主要通过短时分数阶傅里叶变换、Radon变换、希尔伯特变换等高阶矩阵变换技术,提取干扰的时域、频域、调制域等特征,实现对干扰典型参数的估计。从目前公开的文献来看,现有的干扰参数估计方法主要集中在间歇采样干扰(Interrupted Sampling and Repeater Jamming, ISRJ)、切片重构(Chopping and Interleaving, C&I)干扰和频谱弥散(Smeared Spectrum, SMSP)干扰上。
与全脉冲转发干扰相比,间歇采样干扰具有延迟小、响应快、先于真实目标形成假目标等特点,已经得到了广泛应用。文献[13]分析了间歇采样干扰的交叉模糊函数(Cross Ambiguity Function, CAF),提出了一种基于多普勒补偿处理的ISRJ识别方法。文献[14]分析了间歇采样转发式干扰的脉冲压缩时频特性,提出了一种去卷积处理的切片宽度估计方法。文献[15]提出了一种基于短时分数阶傅里叶变换的估计方法,实现对间歇采样干扰的切片个数、切片宽度和调频斜率等干扰参数的估计。文献[16]分析了干扰匹配滤波后互模糊函数的特性,提出了一种基于Radon变换和最小二乘的参数估计方法。文献[17]提出一种滑动截断匹配滤波方法。文献[18]构造了间歇采样转发干扰和接收窗函数的非线性优化模型,提出了基于交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)的干扰参数估计方法,提取切片宽度和数量。文献[19]提出了一种基于希尔伯特变换的估计方法,提取干扰采样次数和转发次数。针对C&I干扰,文献[20]提出了基于短时傅里叶变化的干扰参数估计方法,在干扰脉冲压缩结果的基础上,采用时频分析方法实现了对C&I干扰的切片次数、转发次数和采样时间的有效估计。针对SMSP干扰,文献[21]提出了基于短时傅里叶变换的干扰参数估计方法,在干扰信号能量高于目标回波的前提下,通过时频分析方法实现对SMSP干扰子脉冲个数的估计。
上述方法都仅适用于比较理想的干扰环境,当雷达同时接收到多个间歇采样干扰时,浅层特征估计的难度会急剧增加。同时,地海杂波的存在也会导致干扰参数估计的复杂度增加。因此,还需要进一步进行深入研究。
2.2 干扰深层特征估计技术
干扰深层特征估计主要是利用深度神经网络的特征提取能力,将干扰信号的低维特征变换到高维特征空间,并结合分类器和检测器完成干扰特征的解码,实现干扰类型的识别和参数估计。
文献[22]提出一种基于两个卷积神经网络级联的干扰类型判别方法,分别利用单周期时频图像完成干扰预分类,多周期合成时频图像完成干扰细分类,实现了8种典型干扰样式的识别。文献[23]提出了一种基于残差卷积网络和功率谱特征联合的干扰识别方法,实现了对10种压制干扰的类型识别。文献[24]提出了一种基于剪枝的快速复值卷积神经网络(Fast Complex-Valued Convolutional Neural Networks, F-CV-CNN)的识别方法,提高了干扰识别速度和精度。文献[25]基于提取拖引干扰的特征和信号的前后时序,提出一种基于长短期记忆网络的拖引干扰识别方法。上述方法仅考虑了单域特征,对复杂多干扰的识别效果较差。文献[26]提出了一种基于多卷积分支网络融合的干扰识别方法,通过融合干扰多域特征,实现了多干扰的有效识别。文献[27]提出了一种基于时频域和距离-多普勒域特征融合的识别方法,实现了对12种有源欺骗组合干扰的识别。
上述方法适用于训练数据充足的情形。当训练样本有限时,神经网络将出现过拟合问题,识别性能会急速下降。文献[28]和文献[29]分别提出了一种基于孪生网络的干扰类型识别方法,以及基于加权集成卷积神经网络(Weighted Ensemble Convolutional Neural Networks, WECNN)和迁移学习联合的识别方法,可实现在小样本条件下干扰有效识别。
3. 认知智能雷达抗干扰发射技术
认知智能雷达发射端抗干扰主要是利用实时感知的干扰方位、功率、调制样式以及转发规律等信息,认知最优化设计波形和波束等发射资源,提升电磁对抗环境中抗干扰探测能力。
3.1 抗干扰发射波形设计
在干扰识别后,需根据认知抗干扰策略,在波形库中选择或自适应生成某种波形以有效抑制干扰。文献[30]提出了一种认知雷达抗干扰综合波形优化设计框架,限制发射波形信噪比(Signal-to-Noise Ratio, SNR)、能量、功率谱密度约束的同时最大化互信息(Mutual Information, MI),实现了输出SNR和目标参数估计性能的折中平衡。
针对有源DRFM干扰,本节后续分别根据压制、欺骗和灵巧干扰回波类型,对现有认知抗干扰波形设计方法进行了归纳。
3.1.1 抗压制干扰波形设计
压制干扰主要是通过发射大功率类噪声信号,抬高雷达接收回波中噪声基底,其本质是减小目标检测时的信噪比,降低目标检测概率。
针对已有先验信息的噪声调幅干扰,文献[31]提出了一种基于干扰和旁瓣均衡抑制的发射波形与接收滤波器联合设计方法,通过最小化目标参数的估计误差,提升主瓣比约束下目标检测性能。在此基础上,文献[32]从模糊函数角度出发,提出了一种二维调制抗干扰优化准则,利用交替迭代法求解该优化问题,从距离和多普勒维抑制干扰。
在感知杂波和干扰信息的条件下,文献[33]基于二次型规划迭代计算,提出了一种恒模序列和滤波器联合设计的方法,通过降低目标参数估计的均方误差,降低了压制干扰的影响。文献[34]提出了一种基于最小均方误差准则的发射波形设计方法,主动分配工作带宽能量补偿干扰和杂波影响,增强了雷达抗干扰探测能力。文献[35]以信噪比作为设计指标,提出了一种基于松弛和循环优化的算法,引入低秩重参数,设计多发多收(Multiple-Input-Multiple-Output, MIMO)雷达的多相位波形,能够在认知干扰的条件下保证雷达良好的探测性能。
3.1.2 抗欺骗干扰波形设计
欺骗干扰是指DRFM电子干扰系统捕获到雷达信号后,通过延时、多普勒频率调制等产生与目标回波相似的干扰信号并按照一定规律转发,从而形成多个具有虚假时延或多普勒调制的多假目标,极大增加雷达的虚警概率,降低对真实目标的检测概率。
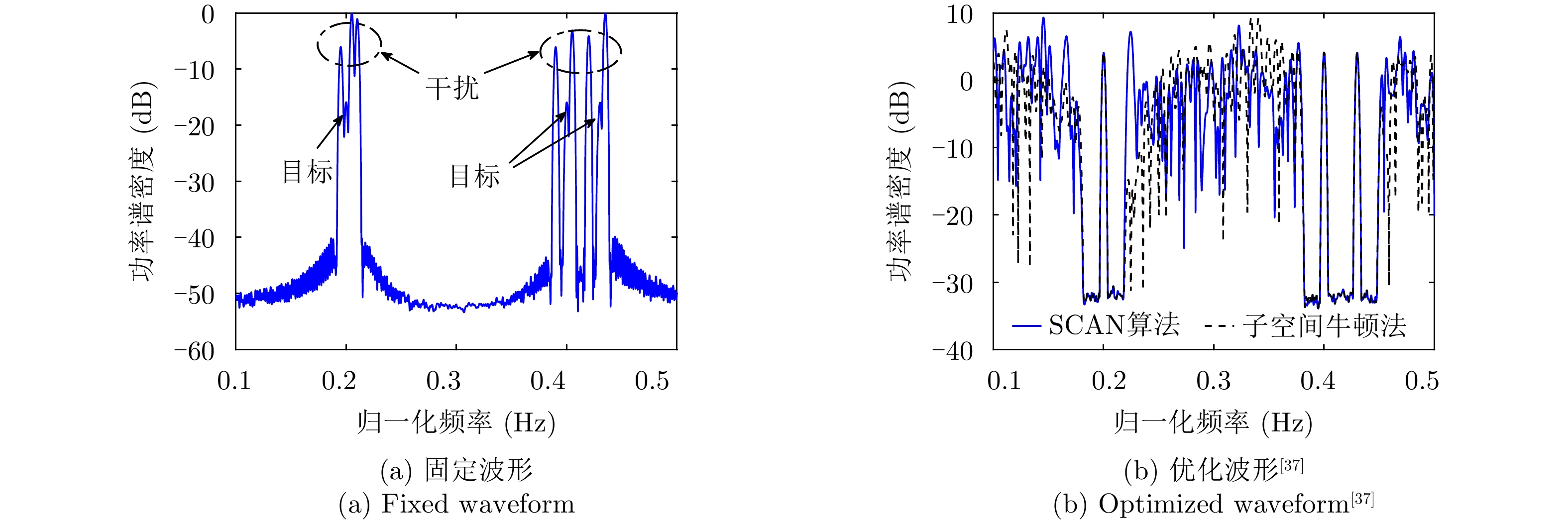
针对速度欺骗干扰,Zhang等人[36]提出了一种脉冲初始相位优化的波形设计方法,在感知目标和干扰的多普勒信息后,通过控制假目标回波频谱在单个真实目标回波多普勒谱一定范围内形成零陷,抑制跨脉冲转发式速度欺骗干扰。针对速度欺骗干扰下多目标检测问题,文献[37]提出了一种多阻带脉间初始相位优化的波形设计方法,通过在每个真实目标回波多普勒谱附近设置阻带,提升了速度欺骗干扰下多目标检测能力,其优化问题如下:
minyJ,αC(yJ,α)=‖˜yJ−Gα‖2s.t.yJ(n)=|Γ(n)|ejθ′n,n=1,2,⋯,N (1) 其中,C为干扰阻带能量;
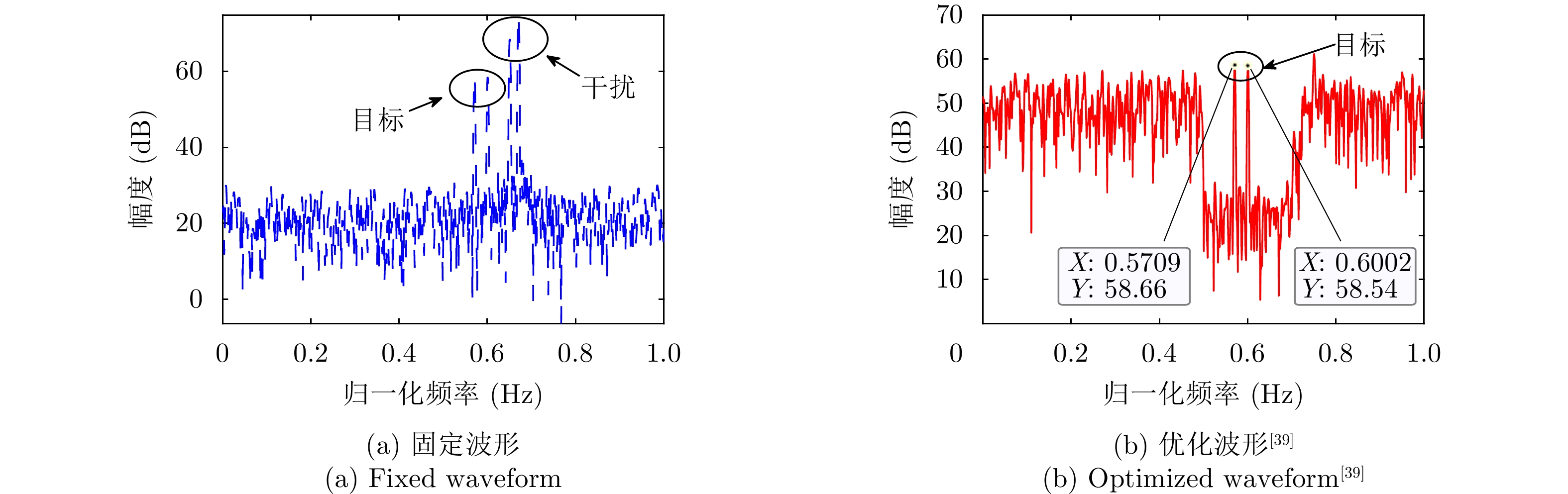
α 为辅助变量;yJ=[yJ(1) yJ(2) ⋯ yJ(N)]T ;(⋅)T 表示转置;|⋅| 表示取模运算;‖⋅‖ 表示二范数;yJ(n) 为第n个接收脉冲内的干扰信号在τd 处的匹配滤波输出;τd 为目标的双程延时;˜yJ=[yJ(1) yJ(2) ⋯ yJ(N) 0 ⋯ 0]T∈C˜N×1 ,N为一个相干处理间隔(Coherent Process Interval, CPI)内的脉冲数;˜N 为一个定值,其取值需要确保离散傅里叶变换(Discrete Fourier Transform, DFT)的频率点能密集覆盖设置的阻带范围。Γ(n)=∑Pp=1ApJej2πnˉfpJ ,其中,P为假目标个数;ApJ 为第p个假目标的幅度;ˉfpJ 为第p个假目标的归一化多普勒频率;P,ApJ ,ˉfpJ 为感知的干扰信息。θ′n=arg(Γ(n))+θn ,θn 为第n−1 个发射脉冲和第n个发射脉冲初始相位的差值;G为定义的DFT矩阵的子矩阵。图2给出了采用固定波形和文献[37]中脉间初始相位优化波形抗干扰结果,其中,真实目标个数为3个,其归一化多普勒频率分别为ˉf1d=0.20 ,ˉf2d=0.40 ,ˉf3d=0.43 ,每个目标多普勒附近均有速度假目标干扰,其归一化多普勒频率分别为ˉf1J=0.195 ,ˉf2J=0.205 ,ˉf3J=0.210 ,ˉf4J=0.390 ,ˉf5J=0.405 ,ˉf6J=0.420 ,ˉf7J=0.435 ,阻带为Ω=(0.18,0.22)∪(0.38,0.45) ,干信比(Jamming-to-Signal Ratio, JSR)为16 dB 。仿真结果表明,文献[37]所设计的波形相对于固定波形具有更好的抗干扰特性。Xiong等人[38]采用了不同整数倍的脉冲重复间隔(Pulse Repetition Interval, PRI)的多通道处理,提出了一种自适应初始相位的波形设计方法,实现了对单/多目标检测下速度欺骗干扰的抑制。文献[39]推导了速度欺骗干扰特性,通过发射随机初始相位的脉冲串对抗速度欺骗干扰。在感知到目标多普勒频率和干扰信号滞后时间等信息的条件下,提出了基于脉间相位捷变的恒模离散相位波形设计方法,提高了速度欺骗干扰下雷达探测能力,其优化问题如下:
minsCJ(s)s.t.|s(m)|=1args(m)=Φ,m∈{1 2 ⋯ M} (2) 其中,
s=[ejφ1ejφ2 ⋯ ejφM]∈CM×1 为设计的发射波形;CJ(s) 表示欺骗干扰在阻带内的能量;Φ={0 1 ⋯ L−1}2π/L 为有限相位集;L为离散相位个数;M为脉冲个数。图3给出了采用固定波形和文献[39]中脉间相位捷变优化波形的抗干扰结果,其中,目标个数为2个,其归一化多普勒频率分别为fT1=0.57 ,fT2=0.60 ,干扰信号的归一化多普勒频率分别为fJ1=0.67 ,fJ2=0.65 ,阻带范围设置为Ω=[0.5,0.7] ,干信比分别为JSR1=10 dB ,JSR2=16 dB 。仿真结果表明,文献[39]中的脉间相位捷变优化波形相对于固定波形具有更好的抗干扰特性。文献[40]增加了脉间波形幅度自由度,考虑波形离散相位和峰均功率比(Peak-to-Average power Ratio, PAR)约束,提出了一种基于最小化阻带范围内干扰能量与目标旁瓣能量加权和准则的脉间幅相联合设计方法,通过非精确交替方向惩罚法(Inexact Alternating Direction Penalty Method, IADPM)求解问题,其优化问题如式(3)所示,
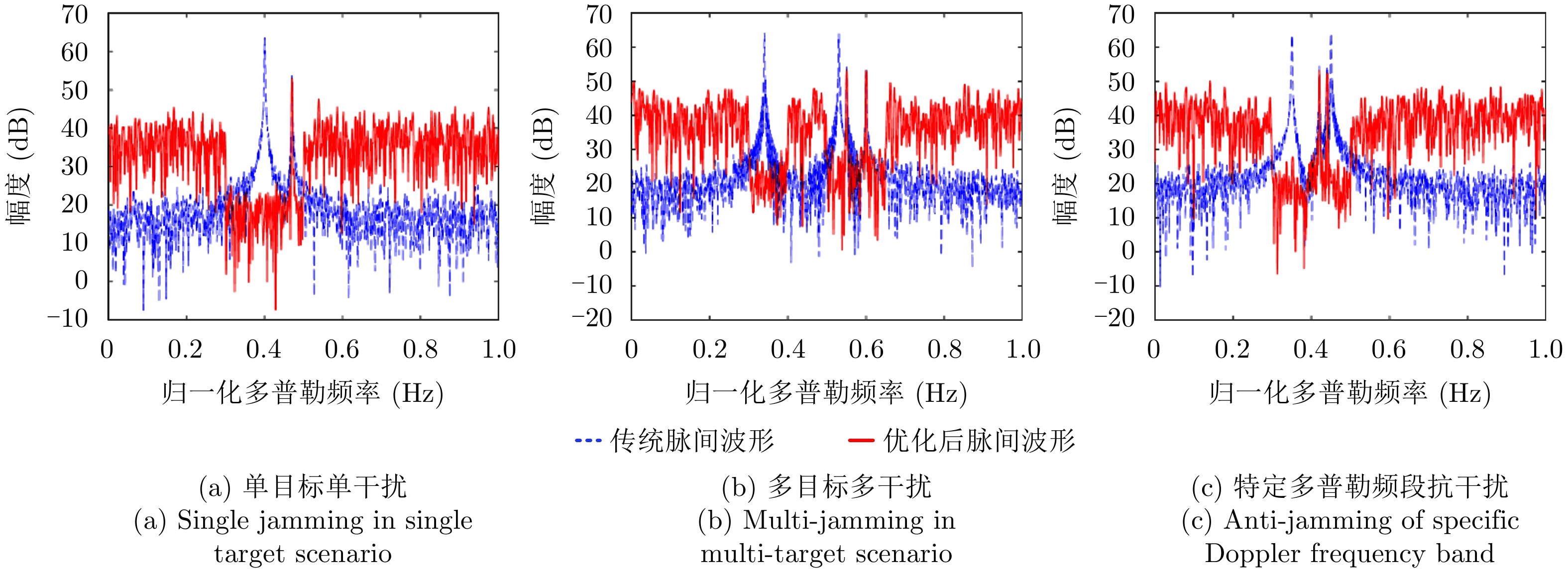
minsf(s)=μ1sHRJs+μ2(J|s|)HRT(J|s|)s.t.PAR(s)≤γ2sHs=Nargsn∈{0 1M2π⋯ M−1M2π},∀n (3) 其中,
s=[s1s2⋯sN]T 为设计的发射波形;N为序列个数;M为离散相位个数;(⋅)H 表示共轭转置操作;μ1,μ2 为权重因子,满足μ1,μ2∈[0,1] ,且μ1+μ2=1 ,用来折中干扰能量和目标旁瓣能量的优化力度;sHRJs 为干扰信号在特定多普勒频段内的能量;(J|s|)HRT(J|s|) 为目标信号在特定多普勒频段内的旁瓣能量;RJ ,RT 分别为求解干扰在特定频段内的能量和目标信号在特定频段内的旁瓣能量时定义的矩阵。图4给出了文献[40]中部分仿真结果,其中,干信比为JSR = 10 dB ,图4(a)目标的归一化多普勒频率fT=0.47 ,干扰信号归一化多普勒频率fJ=0.40 ,特定多普勒频段范围Ω=[0.3,0.5] ;图4(b)目标的归一化多普勒频率分别为fT1=0.42 ,fT2=0.44 ,干扰信号归一化多普勒频率分别为fJ1=0.35 ,fJ2=0.45 ,特定归一化多普勒频段范围为Ω=[0.3,0.5] ;图4(c)目标的归一化多普勒频率分别为fT1=0.55 ,fT2=0.60 ,干扰信号归一化多普勒频率分别为fJ1=0.34 ,fJ2=0.53 ,特定多普勒频段范围为Ω=[0.30,0.40]∪[0.50,0.65] 。仿真结果表明,文献[40]所设计波形在有效抑制虚假目标尖峰的同时可以检测到真实目标。上述方法主要考虑抑制干扰在目标频率附近范围的能量,Feng等人[41]在感知干扰频段等信息后,考虑了最小化发射信号在干扰频段内的频谱幅度,提出了一种谱逼近松弛交替投影的恒模波形设计方法,生成具有低距离旁瓣和指定频谱功率抑制的波形。
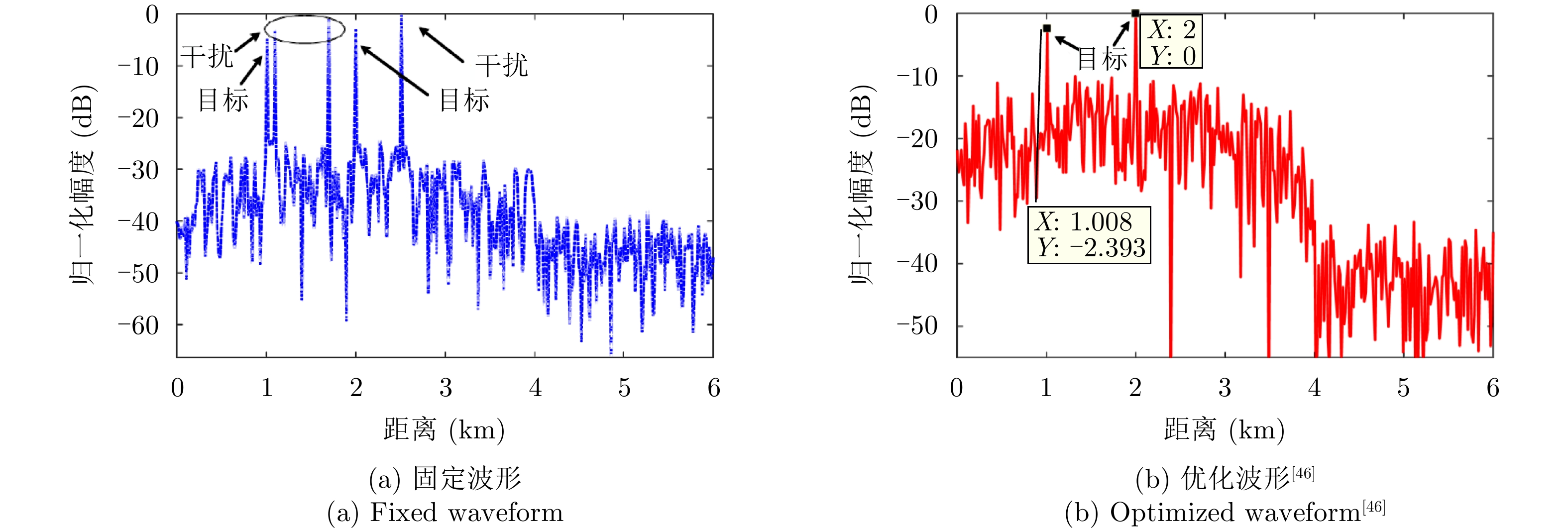
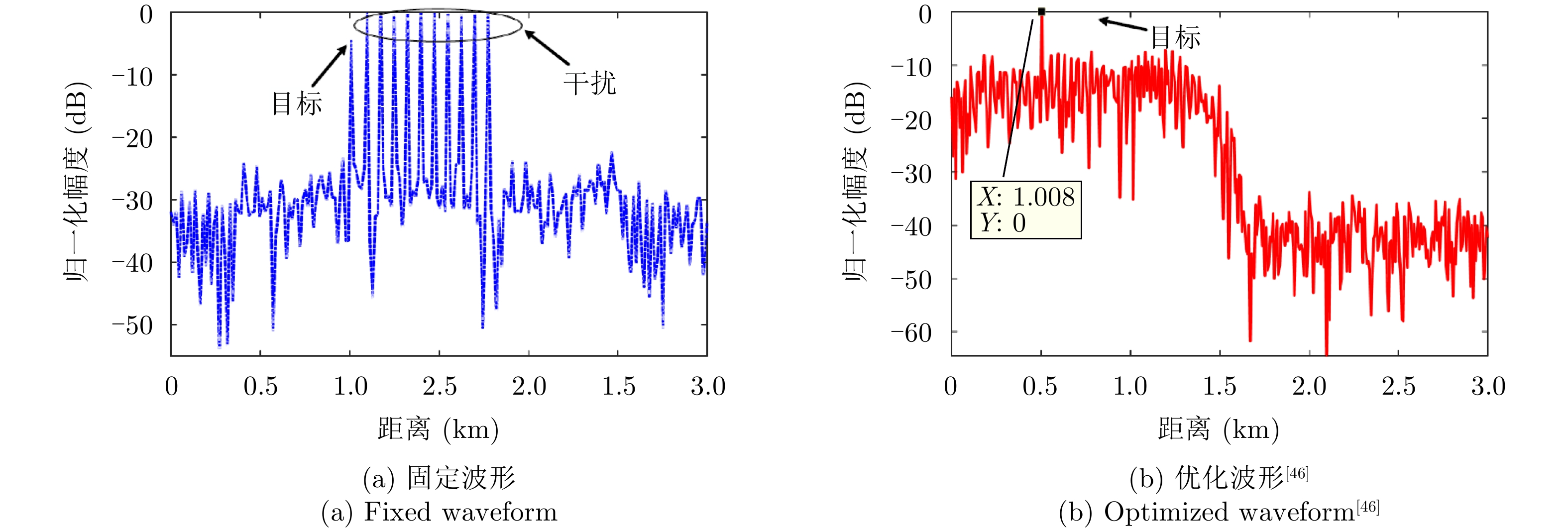
针对滞后目标回波信号至少一个脉冲重复时间(Pulse Repetition Time, PRT)的距离欺骗干扰,文献[42]通过预测DRFM干扰方式,提出了脉间波形分集理论,考虑了不同PRT发射调频斜率随机扰动的线性调频(Linear Frequency Modulation, LFM)波形,抑制距离欺骗干扰。在此基础上,文献[43,44]提出了基于脉冲正交波形的距离欺骗干扰抑制方法。当感知到干扰信号滞后时间等信息时,文献[45]通过在特定的距离区间内形成阻带,提出了一种最小化自相关旁瓣和互相关能量的正交波形设计方法。文献[46]提出了基于最小化积分旁瓣准则的恒模波形设计方法,并采用了基于降阶的4次序列迭代算法求解问题,其优化问题为
minsf(s)=WAISL+WCISLs.t.|s(n)|=1,n∈{1 2⋯ NM} (4) 其中,s为设计的发射波形,
WAISL 为所有设计波形的加权自相关积分旁瓣电平,WCISL 为加权互相关积分旁瓣电平,N为码片个数,M为相位编码信号个数。图5给出了采用固定波形与文献[46]中优化波形在多目标多距离欺骗干扰场景下抗干扰结果,其中,目标距离分别为RT1=1000 m ,RT2=2000 m ,目标信噪比分别为SNR1=22 dB ,SNR2=24 dB ,距离欺骗假目标分别位于RJ1=1100 m ,RJ2=1700 m ,RJ3=2500 m ,干噪比(Jamming-to-Noise Ratio, JNR)分别为JNR1=22 dB ,JNR2=24 dB ,JNR3=25 dB 。图6给出了采用固定波形与文献[46]中优化波形在密集复制假目标干扰场景下单目标探测结果,其中,目标距离RT=1000 m ,干扰机以0.5 μs的间隔连续转发10个密集复制假目标,干噪比为JSR=4 dB 。仿真结果表明,文献[46]中优化波形在这两种场景下具有更好的抗干扰性能。文献[47]在识别干扰样式的条件下,提出了通过信噪比和互信息准则联合设计或选择发射波形的方法,将波形能量集中于最优的接收频段,从理论上分析了抗干扰性能。文献[48]从模糊函数的角度,通过在距离-多普勒范围内最小化干扰和信号旁瓣,提出了正交线性调频-相位编码(Linear Frequency Modulation-Phase Coded, LFM-PC)捷变的抗干扰波形设计方法。文献[49]通过脉间PRI和初相等参数伪随机跳变,提出了一种基于距离门对齐的非均匀相参处理方法,保证了目标的相参积累能力,可以实现对欺骗干扰的抑制,并且具有良好的抗杂波效果。
3.1.3 抗灵巧干扰波形设计
灵巧干扰主要是指干扰机对截获到的雷达信号进行相对复杂的调制重组,形成具有压制和欺骗双重效果的一类干扰。
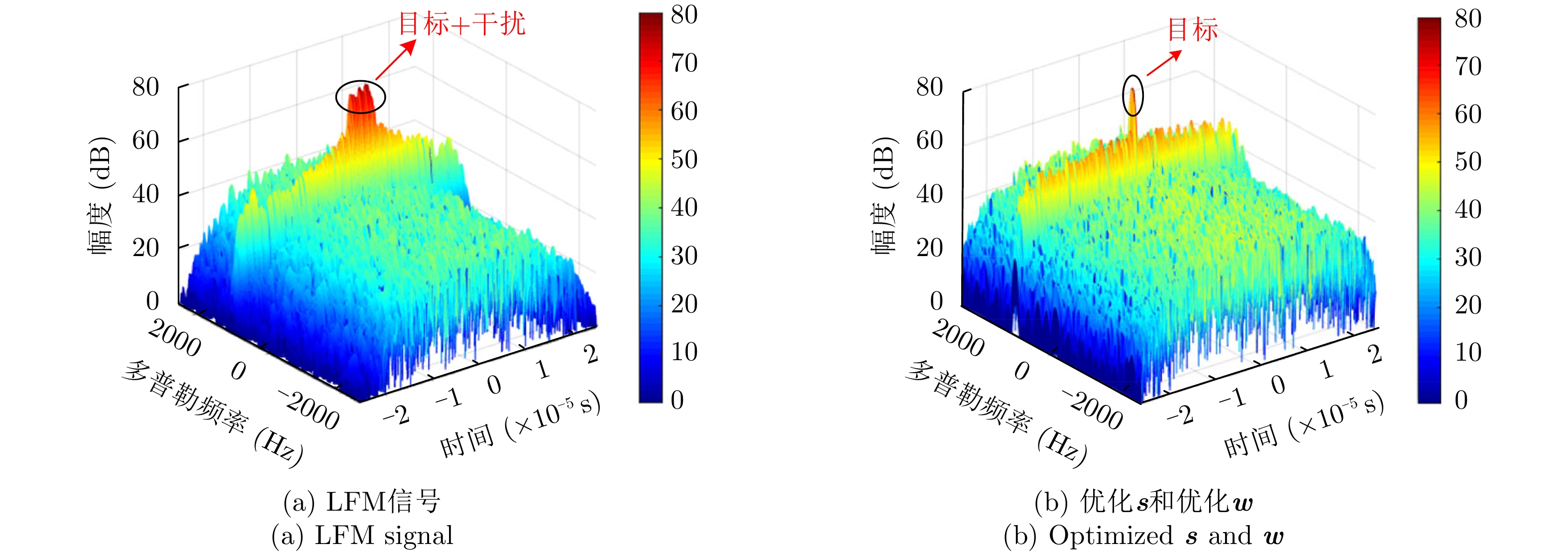
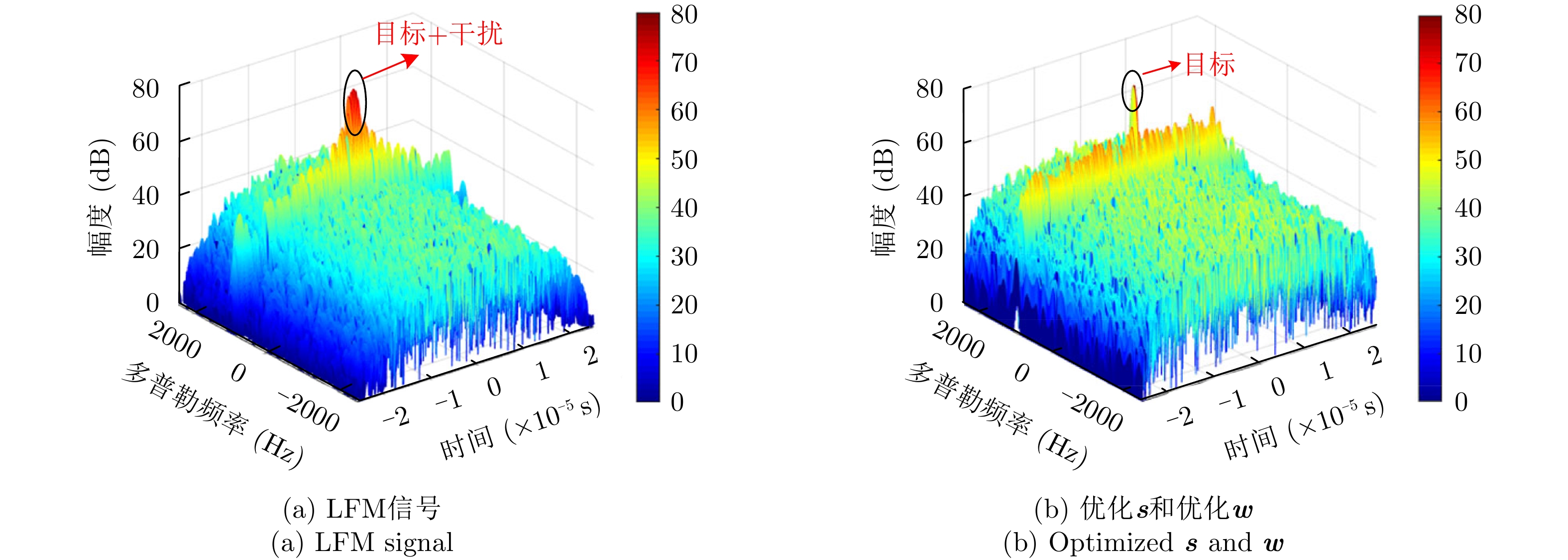
周超等人[50]通过对脉压结果进行短时傅里叶变换分析,获取干扰信号时频分布,设计了一种时频域滤波器实现了对间歇采样转发干扰的抑制。文献[51]在精确认知干扰信号的条件下,考虑PAR约束,提出了一种最小化目标信号与接收滤波器的积分旁瓣电平,以及干扰信号与接收滤波器的积分电平的波形设计方法。该方法无法保证干扰信息存在偏差时的抗干扰性能和算法的收敛性。针对干扰信息存在误差情况,何金阳等人[52]根据感知的干扰采样宽度、重复转发次数和干扰机放大倍数,推导了受间歇采样转发干扰下的雷达回波信号,提出了一种基于最小化积分旁瓣电平准则的恒模波形设计方法,分析了抑制间歇采样转发干扰的有效性。Ge等人[53]提出了基于解耦交替方向惩罚法(Decoupled Alternating Direction Penalty Method, DCADPM)的发射波形与接收滤波器联合设计算法。在干扰置零、恒模和信噪比等约束下,通过最小化目标信号和干扰信号与接收滤波器的积分旁瓣电平的加权和,实现了对灵巧电子干扰的抑制,其优化问题如下:
mins,wμ1ISL(s,w)+μ2ISL(sJ,w)s.t.(1)sHRwj0s≤η或wHRsj0w≤η(2)|s(k)|=1,∀k(3)wHs=N(4)N2‖w‖2≥δ (5) 其中,
Rwj0=1/P∑PJHPwwHJP ,Rsj0=1/P⋅∑PJHPssHJP ;P为干扰机采样时长估计误差离散的采样间隔点;JP 为第P个采样点对应的干扰转移矩阵;s为发射信号;sJ 为干扰信号;w为接收滤波器;μ1,μ2 为权重因子,满足μ1,μ2∈[0,1] ,且μ1+μ2=1 ;约束(1)为干扰置零约束,约束(2)为恒模约束,约束(3)为主瓣电平约束,约束(4)为当噪声功率σ2=1 时的SNR约束。图7—图9给出了所设计的发射波形和接收滤波器对间歇采样转发干扰的抑制效果,其中,干扰信号延迟目标信号1 μs。仿真结果表明,使用优化波形及优化接收滤波器可以实现更好的抗干扰效果。除了通过波形设计直接抑制干扰信号外,部分学者还研究了利用发射信号对干扰信号进行特征分析,然后通过处理方法消除干扰影响。例如:文献[54]提出了一种脉内正交的线性调频-相位编码波形,通过多子干扰信号滤波处理,抑制间歇采样转发干扰。文献[55]设计了一种脉内频率正负交替变化波形,通过短时傅里叶变换估计干扰机采样间隔,设计时域滤波器去除干扰信号。文献[56]在正确感知干扰采样周期、占空比信息的条件下,提出了一种自适应波形参数对抗间歇采样转发干扰的方法,通过调整雷达发射信号脉宽、掩护脉宽等参数,最大化避开被干扰采样的概率。文献[57]设计了一种自适应参数调整的脉内频率编码信号和时域带通滤波器处理方法,抑制间歇采样转发干扰,但是该方法不能适用多目标或多干扰。文献[58]提出了一种基于分数阶傅里叶变换的并行干扰抑制算法,首先对被干扰的脉冲进行切片处理,然后在分数阶傅里叶域利用窄带滤波器组对干扰进行抑制。文献[59-61]利用频率捷变的思想设计波形,在干扰识别的基础上,通过设计滤波或系数重构处理抑制干扰。
针对切片重构干扰和频谱弥散干扰两种灵巧干扰,Lu等人[62]在感知了干扰调制信息的基础上,提出了以最小化发射信号自相关(加权)积分旁瓣电平,和发射信号与干扰信号的(加权)互相关积分电平为准则的恒模波形设计方法。
针对干扰环境下运动目标检测问题,王福来等人[63]考虑恒模约束、接收机脉压峰值约束以及信噪比约束等,提出了一种高多普勒容忍的多脉冲互补序列和接收滤波器联合设计方法,通过最小化发射序列和接收滤波器的模糊函数旁瓣能量,以及干扰信号和接收滤波器的模糊函数能量,实现了一个CPI内对间歇采样转发干扰的抑制。
3.2 抗干扰发射波束形成
发射波束形成主要是指利用雷达目标、敌方侦察机的角度信息,通过设计加权向量以合成期望的发射波束方向图,增强目标方向雷达探测性能,同时降低敌方侦察机方向的辐射能量,减小敌方发现我方雷达的概率。在雷达发射端,一般通过复数加权控制每个阵列天线的增益放大器(或衰减器)和移相器来实现。现有文献主要考虑对权向量施加恒模约束,只对权向量的相位进行优化设计,具有系统结构简单、系统成本低以及功放效率高等优点。
Angeletti等人[64]基于Zernike多项式与入侵杂草优化算法,提出了一种恒模约束下大型平面阵权向量设计方法。刘肖萌等人[65]提出了一种基于投影矩阵法的波束形成方法,能够满足复系数、仅相位、仅幅度优化的波束形成需求。Aslan等人[66]在每一次迭代优化中,通过引入相位扰动将恒模约束非线性问题转化为线性问题求解,并以最小化峰值旁瓣电平(Peak Sidelobe Level, PSL)为优化模型完成了权向量设计。Zhao等人[67]基于径向基函数神经网络,解决了恒模约束下方向图置零问题。Zhang等人[68]将权向量幅值的动态范围(Dynamic Range Ratio, DRR)引入到最小化PSL的优化问题中,采用主对偶方法迭代优化PSL(DDR=1即为恒模约束)。Kajenski[69]考虑主瓣增益,提出了两种恒模约束下权向量设计模型:模型1通过设计权向量最小化阵列增益损失;模型2在给定增益损失条件下最小化局部区域的零陷电平;并使用半定规划(Semi-Definite Programming, SDP)算法完成了发射权向量设计。Fuchs[70]通过对主瓣电平与旁瓣电平施加不同的幅度响应约束,采用SDP算法计算满足恒模约束条件的权向量。但是该方法在幅度响应边界选择不合适的情况下,波束图形状可能会发生恶化。为了避免该问题,Liang等人[71]通过对幅度响应边界施加加权系数来增加权向量优化的自由度,优化问题如式(6)所示,其中,
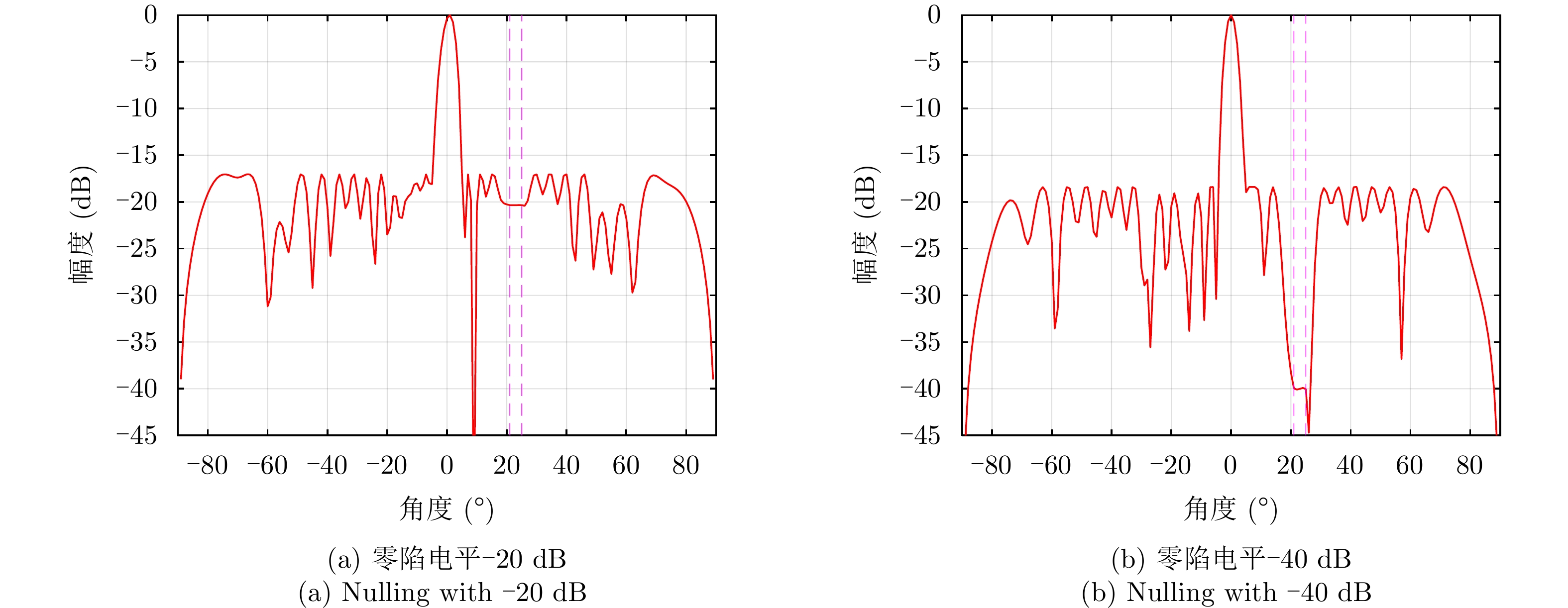
|wn|=An 表示恒模约束;μ 为幅度响应边界加权系数;μL(θ1) 与μU(θ1) 分别为θ1 方向幅度响应的上界与下界。结果表明,该方法不仅可以在指定方向产生深零陷,而且可以灵活控制主瓣宽度与动态范围。maxw,μ μs.t. μL(θs)≤|wHa(θs)|2≤μU(θs),θs∈Θs|wn|=An,n=1,2,⋯,N (6) Gemechu等人[72]以最小化峰值旁瓣电平为优化模型,通过对不同旁瓣区域施加幅度响应约束,实现了对发射方向图旁瓣的灵活控制。图10给出了文献[72]的部分仿真结果,其中主瓣指向
0∘ ,旁瓣控制区域为[21∘,25∘] ,旁瓣控制电平分别设置为–20 dB, –40 dB,其他旁瓣区域为[−90∘,−5∘]∪[5∘,20∘]∪[25∘,90∘] ,乘法因子ρ1 ,ρ2 ,ρ3 分别设置为1, 30, 1。仿真结果表明,该方法能够实现对旁瓣电平的精准控制。4. 认知智能雷达抗干扰接收技术
认知雷达接收端抗干扰主要是通过在空域、时域、频域、极化域设计接收滤波器,实现对目标回波能量积累的同时,抑制干扰信号能量。相关技术主要分为认知抗干扰接收波束形成(空域滤波)以及时域滤波、多普勒域(频域)滤波、极化域滤波以及多域联合滤波。
4.1 空域抗干扰接收波束形成
空域接收波束形成主要是指利用目标/干扰的角度信息,通过设计空域滤波器,对目标方向信号进行能量积累,同时抑制干扰方向的信号能量,可分为静态波束形成与自适应波束形成。
针对静态波束形成,加窗技术具有计算复杂度低、实时处理能力强等特点,在低旁瓣接收波束形成抗全域干扰中被广泛应用,经典的窗函数有切比雪夫窗[73]、泰勒窗[74]等,近年来,有大量的学者对窗函数设计进行了深入研究[75-80],其中Lim等人[79,80]提出了一种主瓣宽度与旁瓣电平权衡技术,提高了传统窗函数的灵活性。
但是传统加窗技术只能应用于均匀阵列。针对任意结构阵列,智能优化算法(遗传算法[81]、模拟退火算法[82]、粒子群算法[83]等)和基于自适应阵列理论的算法[84-88]被应于设计期望形状的波束方向图。张学敬提出了A2RC(Accurate Array Response Control)波束形成算法[85]、MA2RC(Multipoint Accurate Array Response Control)波束形成算法[86]、权向量正交分解波束形成算法[87]等,该类方法可以灵活控制波束方向图的幅度响应。文献[89-92]提出了基于模板匹配的接收波束图设计方法,该类方法的数学模型可以表示为
minεs.t. ||P(θ)|−|Pd(θ)||≤ε (7) 其中,
Pd(θ) 表示预先设定的方向图模板;P(θ) 表示优化方向图。通过预先设定方向图模板形状,并最小化P(θ) 与预设模板的误差,实现对波束方向图形状的灵活控制。然而,模板匹配方法依赖于预设模板,预设模板旁瓣水平设置太低或者太高、主瓣宽度设置太窄或者太宽可能会导致方向图性能恶化。为了避免模板匹配中模板设置不合理问题,Liang等人[93]提出了一种能量约束下最小化最大副瓣电平与最小主瓣电平比值的优化方法:minw maxθs|wHa(θs)|2minθm|wHa(θm)|2s.t. wHw=1 (8) 其中,w表示拟优化设计的权向量;
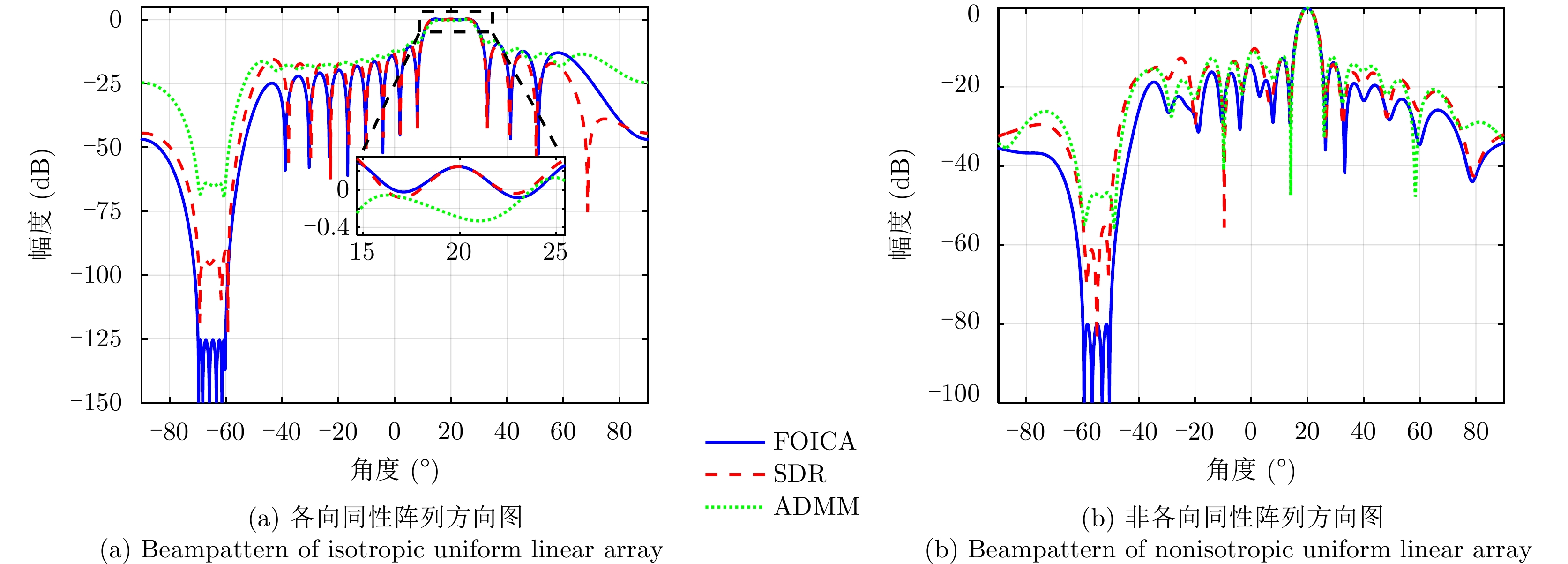
a(θm) ,a(θs) 分别表示主瓣区域、旁瓣区域的导向矢量。wHw=1 约束了滤波器输出能量为常数,可以有效避免权向量幅度模糊问题。该方法针对任意线性阵列、矩形面阵阵列,可以灵活控制主瓣与旁瓣电平,实现低旁瓣波束形成抗干扰的效果。Zhang等人[94]将主瓣增益引入到接收波束形成设计问题,提出了两种优化模型:模型1通过设计权向量最小化阵列增益损失;模型2在给定增益损失条件下最小化局部区域的零陷电平,通过半正定松弛(Semi-Definite Relaxation, SDR)法与拟凸优化寻找优化问题的次优解,实现方向图低旁瓣/深零陷设计。Lu等人[95]同时考虑主瓣增益约束与能量约束,以最小化峰值旁瓣电平为代价函数,并使用1阶迭代凸逼近(First-Order Iterative Convex Approximation, FOICA)算法分别对各向同性、非各向同性天线的接收波束形成权值进行优化设计,优化模型如式(9)所示。minw,η ηs.t. |wHa(θs)|2≤η,θs∈ΘSα≤|wHa(θm)|2≤β,θm∈ΘMwHw=1 (9) 其中,
α ,β 分别表示主瓣增益的下限与上限,ΘM ,ΘS 分别为主瓣角度区间、旁瓣角度区间。图11为文献[95]中零陷设计仿真结果,其中图11(a)为各向同性天线优化方向图,参数设置为:ΘM=[15∘,25∘] ,ΘS=[−70∘,−60∘] ,α=7.5dB ,β=8.0dB ;图11(b)为非各向同性天线优化方向图,ΘM=0∘ ,ΘS=[−60∘,−50∘] ,α=−47.43dB ,β=−47.13dB 。仿真结果表明,相对于ADMM与SDR算法,通过使用FOICA算法对问题(9)进行求解,对于各向同性天线与各向异性天线都可以得到更深的零陷,从而实现更好的抗干扰性能。Liu等人[96]针对分布式相控MIMO雷达,研究了一种子阵布局与接收权向量联合设计方法,同时兼顾子阵位置与主瓣电平约束,实现了接收方向图低旁瓣设计。自适应波束形成技术是通过利用接收信号优化设计加权向量,在增强期望方向信号能量的同时,自适应地在干扰方向形成零陷。Capon在文献[97]中提出了最小方差无失真响应(Minimum Variance Distortionless Response, MVDR)波束形成器设计方法,如式(10)所示。
minw wHRws.t. wHa(θ)=1 (10) 其中,R表示接收信号的协方差矩阵。MVDR在保证期望方向信号无失真通过的条件下最小化波束形成器的输出能量,抑制干扰能量。Wang等人[98]提出了一种自适应稀疏阵列波束形成器设计策略,可根据动态环境快速调整阵列配置和权向量以增强干扰抑制。
考虑在实际应用中,阵列校准存在误差会引起导向矢量失配,此时自适应波束形成器会将期望信号当作干扰信号进行抑制,使得雷达性能严重下降。为了提高自适应波束形成的稳健性,文献[99,100]提出了对角加载技术,并基于白噪声增益约束[99],通过迭代模型计算合适的对角加载参数。为了减少迭代模型的计算复杂度,文献[101,102]提出了一种基于特征空间的稳健自适应波束形成器设计方法,需要准确感知干扰源/期望信号源数量等信息。文献[103-106]考虑导向矢量失配情况,分别提出了不同的自适应稳健波束形成方法,其中,Vorobyov等人[103]将式(10)修正为
minw wHRws.t. |wHc|≥1,c∈χ (11) 其中,
χ 表示失配期望方向导向矢量的可能取值集合。式(11)不再要求对单一方向的导向矢量进行固定的无失真响应,而是对于集合给出的所有可能导向矢量的连续体,通过不等式约束来维持期望方向信号的无失真响应,以此提高在导向矢量失配、低信噪比场景下自适应波束形成器的鲁棒性。Liao等人[107-109]提出了多种稳健自适应波束形成方法,在文献[109]中与对角加载技术相结合,计算得到了一种适用于未知互耦情况下均匀线阵自适应波束形成器。4.2 时频极化域滤波抗干扰技术
在时域滤波方面,针对噪声压制类干扰,文献[110,111]利用对数变换分别估计噪声调频和噪声调幅干扰的参数,重构干扰信号,进而在时域上对消干扰。该方法在抑制噪声调幅干扰时,需要干扰载频与雷达载频满足一定条件。在此研究基础上,文献[112]改进了一种抗噪声调幅干扰算法,使适用范围更广。针对C&I干扰和SMSP干扰,文献[113]通过在每个距离单元设计失配滤波器对干扰进行抑制。该方法需要精确感知干扰波形,同时需要对每个距离单元独立设计滤波器,计算量较大。针对间歇采样干扰,文献[14,20]通过时频变换和解卷积操作,估计间歇采样干扰的切片个数和采样时长,然后重构间歇采样干扰波形,最后在时域进行自适应干扰对消。
在多普勒域滤波方面,文献[114]通过在多普勒域上设计失配滤波器,有效地抑制了速度欺骗干扰。文献[115]将其扩展到距离-多普勒联合域上,通过对每个距离-多普勒单元设计失配滤波器,实现距离-速度联合欺骗干扰抑制。但是该方法需要精确感知干扰波形,同时需要对每个多普勒/距离-多普勒单元独立设计滤波器,计算量较大。
极化滤波主要利用雷达目标与干扰极化方式的差异性,设计极化接收通道的加权系数,实现干扰抑制。文献[116]基于反馈环电路,首先提出了自适应极化对消器(Adaptive Polarization Canceller, APC)的技术框架。文献[117]以最小化输出干扰功率为优化准则,提出了自适应极化对消器的迭代滤波算法,有效抑制了噪声压制类干扰,但是该方法仅针对单极化干扰有效。文献[118]提出了“瞬态极化”的概念,并设计了宽带极化滤波法,实现了变极化干扰信号的极化检测、极化估计和抑制。
鉴于单一域抗干扰的局限性,基于时频、空时、空时频等多维联合滤波抗干扰技术逐渐得到广大学者的重视。文献[119,120]针对间歇采样干扰,研究了间歇采样干扰的时频分布,并在时频域上设计了干扰抑制滤波器。文献[121]在此研究基础上,结合信号重构和时频域滤波思想,在多目标环境下抑制了多种类型的间歇采样干扰。文献[122]结合经验模态分解和分数阶傅里叶变换(Fractional Fourier Transform, FrFT),设计了分数阶域干扰抑制滤波器,提高了强干扰下目标检测概率。在空时域联合滤波抗干扰方面,空时自适应处理技术(Space-Time Adaptive Processing, STAP)是较为经典的技术之一。STAP最早被提出来以解决相控阵体制机载预警雷达的杂波抑制问题[123],经过近半个世纪的发展,STAP在抗干扰领域的优势已逐渐在雷达装备中得到显现。文献[124,125]利用STAP,设计波形协方差矩阵,消除了主瓣支援干扰,但是由于该方法不具有距离维(时域)的自由度,当存在自卫式干扰时,难以从回波混合信号中提取真实目标信号。针对频率分集阵列(Frequency Diversity Array, FDA) MIMO雷达,文献[126,127]研究了空时频三维联合滤波抗主瓣干扰方法,该体制雷达引入了时域自由度,能够解决无法对抗自卫式干扰的问题。在极化-空域联合滤波抗干扰方面,文献[128,129]分别研究了完全极化情形和相关干扰情形下极化敏感阵列的抗干扰性能。文献[130]分析了基于特征空间投影算法的交替极化敏感阵列的主瓣干扰抑制性能。这些研究对联合对消抗干扰有积极的意义,同时也存在一个限制:这些方法存在对消后测角保形困难的问题。针对此问题,文献[131]提出一种陷波器,在空域、极化域干扰抑制的同时,实现了对目标的高精度测角。文献[132]所提算法首先在空域产生主瓣保形旁瓣干扰抑制方向图,然后在极化域进行滤波,最终在空-极化域联合进行主瓣干扰抑制,算法提高了主瓣干扰极化的估计准确度,提高了极化滤波的有效性。
5. 认知智能雷达抗干扰处理技术
当干扰信号与雷达目标信号在空时频极等域上差异较小时,接收滤波方法难以将干扰完全滤除,因此需通过信号和数据处理,进一步消除干扰的影响。
5.1 基于信号分离的抗干扰处理
盲信号分离(Blind Signal Separation, BSS)[133,134]算法通过放大干扰与目标在多域上的差异性,实现干扰与目标分离,在抗干扰领域得到了广泛的应用。
针对主瓣压制干扰,文献[135]首次将BSS算法引入到雷达抗干扰中,提出一种基于高斯矩的BSS算法,分离压制干扰和目标信号。文献[136]提出了一种特征矩阵近似联合对角化(Joint Approximate Diagonalization of Eigen-matrices, JADE)的雷达回波信号盲分离算法,并利用匹配滤波处理从分离的信号中正确识别出目标回波。文献[137]利用盖氏圆半径法估计出源信号个数,然后通过JADE盲分离算法抑制干扰。文献[138]提出一种快速独立成分分析算法(Fast Independent Component Analysis, FastICA)的雷达回波信号盲分离算法,并比较了JADE与FastICA两种算法的性能优劣。针对低信噪比条件下BSS抗主瓣干扰方法性能恶化的问题,文献[139]提出一种利用FrFT对BSS后的目标回波降噪处理方法,提高干扰抑制后输出信干噪比。
针对主瓣欺骗干扰,文献[140]将BSS算法应用于欺骗干扰抑制中,通过两个PRT接收回波构造观测数据,利用JADE算法将真实目标回波与干扰回波分离开来。文献[141]将其扩展到多旁瓣干扰、主瓣欺骗干扰和压制干扰同时存在的情况,对空时多通道雷达回波中干扰和目标信号进行盲分离。文献[142]将BSS算法应用于FDA-MIMO雷达中,解决了干扰与目标角度相同时的欺骗干扰抑制问题。文献[143]将BSS算法拓展应用于到分布式组网雷达中,对BSS算法处理后的信号,进一步利用椭圆定位处理剔除剩余干扰虚假点迹。文献[144,145]将联合盲信号分离算法应用于分布式相控阵雷达中,实现目标回波与干扰信号的分离。
针对灵巧类干扰,传统盲分离算法要求被分离的两路信号不相关,这一限制使得对灵巧类干扰的分离变得困难。随着盲分离技术的发展,更多新技术被应用于该领域中。张量作为一种能够体现数据高阶特征的结构近年来被引入盲分离抗干扰的应用中。文献[146]将张量的标准分解运用到盲分离模型中进行混合矩阵估计,通过构造信号时延张量并对该张量进行标准分解,得到盲分离模型中混合矩阵的估计。文献[147]改进了文献[146]的方法,先运用Tucker分解求出时延张量的核张量,后用标准分解,大大加快了算法速度。文献[148]构造4阶累积量张量,并用张量标准分解求解混合矩阵;文献[149]则利用Tucker分解求解混合矩阵。
由于BSS算法不需要精确已知干扰类型和干扰角度,在雷达主瓣抗干扰中具有较大的应用潜力。但是,目前BSS抗主瓣干扰方法仍存在一些问题。当目标与干扰机角度差减小时,两者的线性流形相关性增强,分离性能降低,特别当干扰机角度和目标角度相同时,信号分离的性能会急剧恶化。此时,需要构建更高的维度,例如加入极化信息[150],以保证良好的性能。
5.2 基于特征挖掘的抗干扰处理
基于特征挖掘的抗干扰处理主要是通过挖掘目标回波与干扰信号在幅度、空间散射等维度上的差异性,实现对电子干扰下目标检测识别,主要适用于距离或速度假目标欺骗干扰。
深度神经网络具有良好的特征提取能力,可以用于挖掘干扰信号与目标回波在高维空间的差异。文献[151]将主瓣干扰下的信号方向图作为输入,将期望信号的方向图作为训练目标,利用误差反向传播网络进行训练,可以在方向图中的干扰位置生成较深的零陷。相对于传统方法,该方法产生的零陷对主波束的影响更小、测角精度更高。基于卷积神经网络(Convolution Neural Networks, CNN),文献[152]提出了一种端到端的干扰情景下目标检测网络,增强了间歇采样转发干扰下目标检测性能。文献[153]分析了DRFM电子干扰的量化特性,利用神经网络分类器,识别3位及以下量化位数DRFM欺骗干扰信号。在此基础上,文献[154]进一步分析了DRFM相位量化对干扰信号频谱的影响,提出了一种自适应相关和广义似然比检测算法,利用干扰信号误差角来区分干扰和目标回波信号。文献[155]将其扩展到FDA-MIMO雷达欺骗干扰下目标检测中。该类算法仅适用于DRFM相位量化位数较低情况。当量化位数较高时,干扰信号逼近真实发射信号,目标检测性能会急剧降低。
文献[156,157]利用分布式雷达各接收节点的干扰信号幅度相关性高,而目标回波相互独立的特性,对距离假目标干扰进行检测识别。在此基础上,文献[158]利用真假目标在各接收节点的幅度比差异,提出一种聚类处理方法对抗假目标。文献[159]基于空间散射特性,通过利用真假目标的Hermitian距离的差异性,识别真假目标。文献[160]基于真目标点迹的空间相关性,提出一种同源性假设方法,在定位平面上剔除假目标。文献[161,162]利用真目标与假目标在定位平面和多普勒信息上的差异性,解决距离-速度联合欺骗干扰抑制问题。
近年来,雷达极化学领域中的极化鉴别取得较大进展。极化鉴别指通过对目标信号和干扰信号的极化域特征的提取来区分真假目标,从而实现假目标干扰的抑制。文献[163]通过分析真实目标与假目标的散射特性差异,通过极化散射矩阵的性质对真假目标进行鉴别;文献[164]利用目标回波和干扰信号的瞬态极化投影矢量变化规律区分真假目标;文献[165]针对宽带目标在分时极化测量体制下极化特性变化的特点,研究了高分辨率分时极化测量雷达体制。以上方法均为极化鉴别领域的经典方法,但是他们仍然存在雷达测量体制局限、对测量环境要求苛刻等问题。针对极化测量体制的局限,文献[166]分别讨论在分时极化测量体制和瞬时极化测量体制下的目标鉴别方法。针对无法对抗极化调制干扰的问题,文献[167]建立双机站模型,提取能直接用于鉴别雷达目标和极化调制有源诱饵的特征量,实现对有源诱饵干扰的抑制;当干扰机模拟目标散射特性时,文献[168]通过不断变化发射信号的载频,实现了全极化复杂调制假目标的鉴别。针对实际作战环境,文献[169]分析了弹道中段目标的动态极化特性,有效增强了极化鉴别的准确性。
基于特征挖掘的抗干扰处理方法主要侧重于挖掘干扰与目标在低维度特征空间(时域、空域、多普勒域等)的差异,当目标与干扰在低维特征空间接近时,上述方法将会失效。深度神经网络具备挖掘不同信号高维特征空间差异的能力,通过引入深度神经网络,基于高维特征空间的干扰与目标分辨方法将亟待被开发。
6. 认知智能雷达抗干扰调度技术
认知智能雷达抗干扰调度主要是指基于干扰的认知信息,采用智能调度算法,完成抗干扰决策和资源的高效配置,形成“感知-学习-决策-行动”的反馈闭环,使雷达有效应对外部复杂的电磁环境。同时,抗干扰性能评估也是对抗策略有效性的重要依据。下面将围绕抗干扰智能资源调度与效能评估两方面进行总结。
6.1 抗干扰智能资源调度
灵巧干扰、集群干扰和智能干扰的出现,使得传统被动式、应答式的雷达抗干扰技术已无法应对复杂多变的对抗环境。主动认知智能化抗干扰已成为应对复杂电子干扰的主要研究方向之一。“主动式”体现在雷达发射波形的捷变性和空时频能多域资源的可控性;“认知智能化”体现在雷达能够根据外部环境变化,对发射波形参数和空时频能资源进行智能调度、接收、处理、评估和决策等,在动态对抗环境中形成OODA (Observation-Orientation-Decision-Action)闭环。
因此,资源智能调度技术是认知智能化雷达的关键之一。近年来,国内外学者在资源智能调度方面开展了大量研究,包括波形参数智能调度、功率资源智能调度、频域资源智能调度3个方面。
6.1.1 波形参数智能调度
波形参数智能调度主要是指雷达基于外部环境实时感知结果,决策选择波形样式、波形时空频能等多域参数,动态地自适应调整发射信号,使敌方难以捉摸我方雷达发射策略和意图。
雷达信号的波形选择、参数设置、波束形成以及对抗策略选择,可以利用博弈论原理进行分析。赫彬等人[170]在多基地组网雷达场景下,基于智能博弈理论,提出一种迭代波束形成与功率分配联合优化算法,其中,第
k 个雷达的波束形成和约束信干噪比的优化模型表示为minWt(k)L∑l=1‖wt(kl)‖2,s.t.|wHt(kl)hr(kkl)|2L∑j≠l|wHt(kl)hr(kkj)|2+η−kl≥γ∗kl,∀lwHt(kl)gr(kl)gHr(kl)wt(kl)=0,∀l (12) 其中,
{{\boldsymbol{w}}_{{\text{t}}(kl)}} 为第k个雷达主波束指向第l个目标复发射波束权矢量;Wt(k)表示策略集;{{\boldsymbol{h}}_{{\text{r}}(kkl)}} 表示从第k个雷达的发射信号经过第l个目标后又被第k个雷达接收的通道矢量;{{\boldsymbol{g}}_{{\text{r}}(kl)}} 为第k个雷达的发射信号又返回第k个雷达对应于第l个目标信号的通道矢量;{\eta _{{{-}}kl}} 为与噪声方差相关的量;\gamma _{kl}^* 表示约束最小信干噪比。该方法采用线性约束最小方差准则优化雷达接收波束,抑制了多雷达之间的互干扰,并在信干噪比(Signal-to-Interference plus Noise Ratio, SINR)约束下最小化雷达的辐射功率。Song等人[171]将雷达和干扰之间的对抗行为建模为二人零和博弈过程,分别研究了单边博弈、分层博弈和对称博弈下的最优波形调度策略。Piezzo等人[172]为提高干扰背景下的信干噪比,针对3种不同类型的接收滤波器,提出了一种基于位势博弈的波形分配方案,结果表明,通过对波形的自适应迭代,雷达可以达到纳什均衡策略,最大限度地提高了对抗性能。
Jiang等人[173]针对欺骗干扰下雷达多目标跟踪资源管理问题,建立了基于部分可观测马尔可夫决策过程的博弈模型,提出了一种基于仿真的随机梯度优化算法,提升了雷达在干扰环境下的目标跟踪精度。
此外,智能进化类算法也应用于解决认知智能雷达抗干扰问题。例如:陶庭宝等人[174]针对有源压制性干扰下相控阵雷达多目标跟踪时间资源优化问题,提出一种基于互信息的配置算法,建立了时间资源优化配置模型,并采用改进的遗传算法对模型进行求解,结果表明,可以在有源压制干扰条件下最大化有效跟踪的目标数量。
6.1.2 功率资源智能调度
功率资源智能调度主要是指雷达基于实时感知的战场态势信息,动态地调整发射功率,实现探测与隐身性能的折中。这是因为由于提高发射功率,可以提高雷达抗干扰性能和推远探测威力,但同时也会增加被敌方侦测的风险;降低发射功率虽然能保证低截获电磁隐身性能,但探测性能可能得不到保证。
针对电子干扰环境下功率资源调度问题,基于认知博弈理论,Deligiannis等人[175]研究了干扰环境下的组网雷达的功率分配问题,结合凸优化方法和非合作博弈技术,识别干扰并确定最优功率分配,其功率分配博弈优化模型为
\begin{split} & \mathop {\min }\limits_{{{{\boldsymbol{p}}}_{\text{R}}}} {\text{ }}\sum\limits_{k = 1}^K {{p_{{\text{R}}k}}} \\ & {\text{s}}{\text{.t}}{\text{. }}\frac{{{a_k}{p_{{\text{R}}k}}}}{{\displaystyle\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray}} ^K {{m_{kj}}{p_{{\text{R}}j}} + {l_k}{p_{{\text{J}}k}} + \sigma _{\text{n}}^2} }} \ge {\gamma _k},\forall k \end{split} (13) 其中,
{{{\boldsymbol{p}}}_{\text{R}}} = {[{p_{{\text{R}}1}}\; {p_{{\text{R}}2}}\;\cdots {\text{ }}{p_{{\text{R}}K}}]^{\text{T}}} 为所有雷达的功率分配向量;{m_{kj}} 是雷达k与雷达i之间的雷达通道增益;\sigma _{\text{n}}^2 为噪声功率;{l_k} 为干扰机k的泄露增益;{a_k} 为雷达k从发射机到接收机的信道增益;{\gamma _k} 为雷达k的信干噪比最低要求。同时采用自适应波束形成技术来抑制干扰,有效提高了组网雷达的抗干扰性能。此外,Deligiannis等人[176]还针对分布式MIMO雷达,将博弈理论与凸优化相结合,建立了非合作博弈、部分合作博弈和Stackelberg博弈3种博弈模型,在达到预设探测性能的情况下,最小化雷达的辐射功率。6.1.3 频域资源智能调度
雷达工作频率在脉间或脉组间进行一定范围内快速捷变,使干扰难以瞄准雷达工作频率,可以最大限度地阻隔干扰信号进入雷达接收机。频率智能调度是指雷达实时感知干扰信号频率和干扰样式,在动态交互中学习干扰策略,并自适应调整我方工作频率、带宽和捷变速度等,使敌方干扰难以跟上我方频域变化,是应对战场日益复杂、智能和灵巧干扰的关键技术之一。目前,国内外主要基于深度强化学习和博弈论方法,解决频域资源的智能调度问题。
Li等人[177]针对雷达主瓣抗干扰问题,提出一种基于深度强化学习的频率捷变抗干扰策略设计方法,该方法可对抗多种干扰。针对智能化的干扰,Li等人[178]针对雷达和干扰机之间的动态博弈过程,采用一种神经虚拟自我对局(Neural Fictitious Self Play, NFSP)算法得到近似的纳什均衡策略,验证结果表明其性能优于常用的基本策略和高级策略。
Shi等人[179]针对多基地雷达和MIMO系统的频谱共存问题,提出了基于Stackelberg博弈的鲁棒功率控制算法,确保雷达目标检测以及通信系统的正常运行。在应用中,为多基地雷达和MIMO通信两种系统分别设计了效用函数,大规模MIMO通信的功率分配优化模型为
\begin{split} & \mathop {\max }\limits_{\boldsymbol{\theta }} {{\hat U}_{{\text{com}}}}({\boldsymbol{\theta }},{\boldsymbol{P}}) \\ &{\text{s}}{\text{.t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^{{N_{\text{R}}}} {{P_i}\left( {g{ _{{{\text{d}}_i}}} - {\varepsilon _{{{\text{d}}_i}}}} \right) \le {T_{{\text{th}}}}} \end{split} (14) 其中,
{\hat U_{{\text{com}}}}({\boldsymbol{\theta }},{\boldsymbol{P}}) 为通信基站效用函数;{\boldsymbol{\theta }} 为干扰价格向量;{g_{{{\text{d}}_i}}} 为雷达i到通信基站的直达波;P为雷达发射功率向量;{T_{{\text{th}}}} 为预设的总干扰阈值;{\varepsilon _{{d_i}}} 表示{g_{{d_i}}} 的不确定度界限;{P_i} 是雷达i的发射功率。多基地雷达的功率分配优化模型为\begin{split} & \mathop {\max }\limits_{\boldsymbol{P}} {{\hat U}_{{\text{rad}},i}}({P_i},{{\boldsymbol{P}}_{ - i}},{\theta _i}) \\ & {\text{s}}{\text{.t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat \gamma }_i} \ge {\gamma _{i{\text{min}}}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall i \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {P_i} \le P_i^{{\text{max}}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall i \end{split} (15) 其中,
{\hat U_{{\text{rad}},i}}({P_i},{{\boldsymbol{P}}_{ - i}},{{\boldsymbol{\theta }}_i}) 为雷达i的效用函数;{\hat \gamma _i} 为第i个雷达的SINR;{\gamma _{\min }} 为保证探测性能的最小SINR阈值;P_i^{\max } 是雷达i的发射功率的最大值限制;{{\boldsymbol{P}}_{ - i}} 表示除雷达i外所有雷达的功率分配情况。此外,针对雷达之间或雷达与通信的频谱共享问题,Khan等人[180]针对不同雷达的频谱资源共享问题,建立了位势博弈模型,提出了两种用户接入方案,使得通信用户可以共享雷达资源且不对雷达产生干扰。
6.2 抗干扰效能评估
近年来,国内外学者就雷达对抗效能评估方法开展了大量研究,主要可分为3类,即试验法、仿真法和解析计算法[181-184]。表1对这3类效能评估方法的定义和优缺点作了详细对比,其中解析计算法可结合试验法和仿真法,借助其他数学计算工具,可静态评估雷达对抗效能,具有更好的理论和应用价值。
表 1 基于试验、仿真和解析计算的效能评估方法对比Table 1. Performance evaluation methods based on experiment, simulation, and analytical computation评估方法 实现方式 优点 缺点 试验法 外场试验 实时性好,数据可靠,结果可信 成本高,灵活性差 仿真法 计算机实时仿真 成本低,适应性好,可近似得到外场试验效果 数据可靠性和结果可信度次于试验法 解析计算法 通过数学分析指标之间的关系,建立评估模型,
借助试验和仿真手段,进行量化评估可理论上探讨可能的对抗效能,受资金、设备和技术的制约小 实时性差 解析计算法对抗效能评估包括两个步骤:指标体系构建和指标权值计算。以下分别就解析计算法对抗效能评估的两个步骤做简要概述。
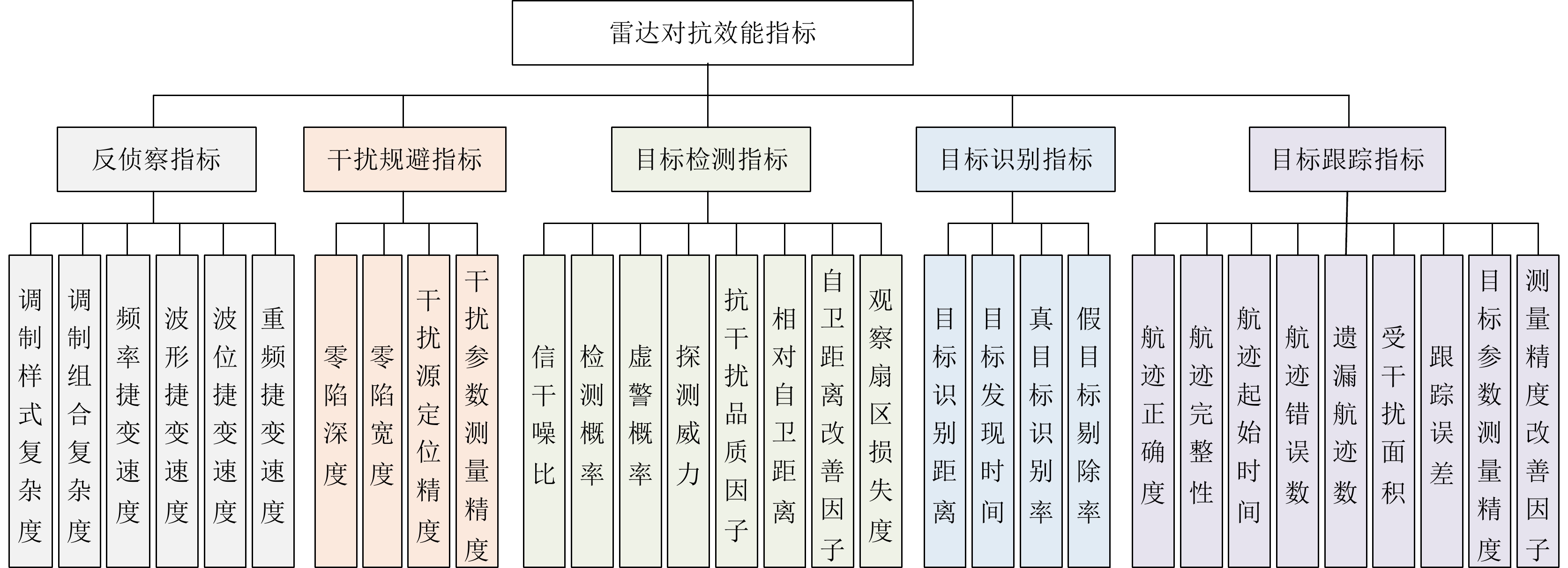
6.2.1 对抗效能指标体系构建
指标体系是评估雷达对抗综合效能的基础。雷达对抗效能指标涵盖多个层面,图12展示的是在反侦察、干扰规避、目标检测、目标识别和目标跟踪层面的雷达对抗效能常用指标[182,185-189]。
体系中的指标并不完全适用于每项作战任务,而是根据雷达的具体作战场景、对抗环境和任务需求,优化选择部分指标用于评估雷达的对抗效能。指标的优化选择需保证完备性、独立性和可用性准则。其中,完备性要求按照多层次、全方面的原则进行指标选择;独立性要求指标之间减少交叉,各指标物理意义明确;可用性要求指标可量化处理,定性指标需通过问题转化,使之可检验、可计算和可测量。
6.2.2 对抗效能指标权值计算
针对具体作战场景、对抗环境和任务需求下的雷达对抗多层级效能评估指标,需充分挖掘各指标的重要性、指标之间的关联性以及冲突性,优化计算能体现各指标重要程度的权重系数,并对各指标进行加权融合,最终得到量化的雷达综合对抗效能指标。
目前,国内外学者对权值计算方法的研究可概括为3个方面:传统加权平均法、模糊层次分析法和智能学习法。
(1) 加权平均法
该方法中各指标权值和指标分数都由专家给定,效能评估结果受主观因素影响较大。
模糊层次分析法能够对一些不能统一度量的对抗效能评估问题进行量化处理,给出一个比较全面客观的评价结果。该方法的步骤包括5个要点:确定指标集、确定权重集、建立评价集、计算模糊综合评价矩阵以及模糊综合算法设计。模糊层次分析法在很大程度上解决了传统加权平均法中主观因素对评估结果的影响。
由于各指标之间的关系错综复杂,需要设计能够描述和表征指标之间的任意非线性映射关系的对抗效能评估方法。因此,基于智能学习算法的雷达对抗效能评估方法应运而生,典型的包括支持向量机[196]和神经网络[197]评估方法。智能学习法削弱了传统加权平均法中主观因素影响,同时能提高模糊层次分析法处理指标之间非线性关系的能力。但是智能学习算法的训练需要足够的样本,在样本不完备情况下评估结果可信度得不到保证。
7. 认知智能雷达抗干扰技术展望
认知智能雷达具有闭环学习自进化的雷达架构,可以适应复杂多变的电磁对抗环境,是未来雷达技术发展的重点方向之一。从公开发表的文献来看,学术界和工业界的技术研究主要还是集中在认知智能雷达的具体核心功能环节,包括环境感知、认知发射和接收、智能处理和资源调度等,而缺乏对闭环系统进行深入和全面的理论与技术研究。同时,随着电磁频谱战技术的不断进步,电子干扰越来越智能化、协同化和一体化,雷达将面临更加复杂的战场电磁环境。因此,从应用需求和技术发展角度,认知智能雷达抗干扰技术具有以下几个发展趋势。
(1) 具备闭环自学习进化能力是认知智能雷达发展的必然趋势
为了应对日益复杂化、智能化和协同化的电子干扰,认知智能雷达任何单个维度的对抗措施都难以适应未来复杂电磁干扰环境。因此,未来军事作战中,雷达需要具备不断学习外部环境,不断与外界环境进行交互,从感知、发射、接收、处理和调度等多环节闭环对抗干扰,且具备自主学习能力,是认知智能雷达发展的主要方向之一。
(2) 与智能化干扰的动态博弈是认知智能雷达即将面临的挑战
未来电磁频谱战中,智能化干扰同时具备截获、分选、调制、转发、学习、决策和评估的功能,在与雷达的动态博弈对抗中,能够对雷达信息进行精准感知,然后经过学习推理,决策生成最优的干扰策略,给雷达探测与生存带来巨大挑战。为了应对智能化干扰,认知智能雷达需引入先进智能博弈技术,在多阶段动态交互过程中,学习并生成最优的博弈对抗策略,以智反智。
(3) 多雷达信号域协同将催生认知智能雷达更强大抗干扰能力
未来信息化作战中将是体系与体系间的对抗。多智能干扰机协同化使雷达面临着空时频极等多域精准覆盖的多样化和复杂化电子干扰,单雷达已经难以有效应对。因此,多雷达信号域协同组网是未来主要研究方向之一[200],主要将多认知智能化雷达的信号多域参数进行协同配置发射,可有效提升信号的复杂性与随机性,破坏敌方干扰机的分选、识别以及决策环节,极大地降低干扰的效能。
-
表 1 基于试验、仿真和解析计算的效能评估方法对比
Table 1. Performance evaluation methods based on experiment, simulation, and analytical computation
评估方法 实现方式 优点 缺点 试验法 外场试验 实时性好,数据可靠,结果可信 成本高,灵活性差 仿真法 计算机实时仿真 成本低,适应性好,可近似得到外场试验效果 数据可靠性和结果可信度次于试验法 解析计算法 通过数学分析指标之间的关系,建立评估模型,
借助试验和仿真手段,进行量化评估可理论上探讨可能的对抗效能,受资金、设备和技术的制约小 实时性差 -
[1] HAYKIN S. Cognitive radar: A way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30–40. doi: 10.1109/MSP.2006.1593335 [2] 崔国龙, 余显祥, 杨婧, 等. 认知雷达波形优化设计方法综述[J]. 雷达学报, 2019, 8(5): 537–557. doi: 10.12000/JR19072CUI Guolong, YU Xianxiang, YANG Jing, et al. An overview of waveform optimization methods for cognitive radar[J]. Journal of Radars, 2019, 8(5): 537–557. doi: 10.12000/JR19072 [3] SHI Yuchun, JIU Bo, YAN Junkun, et al. Data-Driven radar selection and power allocation method for target tracking in multiple radar system[J]. IEEE Sensors Journal, 2021, 21(17): 19296–19306. doi: 10.1109/JSEN.2021.3087747 [4] SHI Chenguang, WANG Yijie, SALOUS S, et al. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 2762–2778. doi: 10.1109/TAES.2021.3138869 [5] ZHANG Haowei, LIU Weijian, ZONG Binfeng, et al. An efficient power allocation strategy for maneuvering target tracking in cognitive MIMO radar[J]. IEEE Transactions on Signal Processing, 2021, 69: 1591–1602. doi: 10.1109/TSP.2020.3047227 [6] YUAN Ye, YI Wei, HOSEINNEZHAD R, et al. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars[J]. IEEE Transactions on Signal Processing, 2020, 69: 443–458. doi: 10.1109/TSP.2020.3047519 [7] BERGER S D. The spectrum of a digital radio frequency memory linear range gate stealer electronic attack signal[C]. 2001 IEEE Radar Conference, Atlanta, USA, 2001: 27–30. [8] BERGER S D. Digital radio frequency memory linear range gate stealer spectrum[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(2): 725–735. doi: 10.1109/TAES.2003.1207279 [9] 李建勋, 唐斌, 吕强. 双谱特征提取在欺骗式干扰方式识别中的应用[J]. 电子科技大学学报, 2009, 38(3): 329–332. doi: 10.3969/j.issn.1001-0548.2009.03.003LI Jianxun, TANG Bin, and LÜ Qiang. Bispectrum feature extraction used in deceptive jamming modes recognition[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(3): 329–332. doi: 10.3969/j.issn.1001-0548.2009.03.003 [10] 田晓, 唐斌. 基于归一化小波分解能量比的雷达有源欺骗干扰识别[J]. 数据采集与处理, 2013, 28(4): 416–420. doi: 10.16337/j.1004-9037.2013.04.001TIAN Xiao and TANG Bin. Active deception jamming recognition of radar based on normalized wavelet decomposition power ratio[J]. Journal of Data Acquisition and Processing, 2013, 28(4): 416–420. doi: 10.16337/j.1004-9037.2013.04.001 [11] 杨少奇, 田波, 李欣, 等. 基于时频图像特征提取的LFM雷达有源欺骗干扰识别[J]. 空军工程大学学报:自然科学版, 2016, 17(1): 56–59. doi: 10.3969/j.issn.1009-3516.2016.01.011YANG Shaoqi, TIAN Bo, LI Xin, et al. A recognition method of LFM radar active deception jamming based on SPWVD figure[J]. Journal of Air Force Engineering University:Natural Science Edition, 2016, 17(1): 56–59. doi: 10.3969/j.issn.1009-3516.2016.01.011 [12] 李紫航, 宋万杰. 有源干扰感知的熵理论方法[J]. 信号处理, 2017, 33(12): 1652–1656. doi: 10.16798/j.issn.1003-0530.2017.12.018LI Zihang and SONG Wanjie. Entropy theory method for active jamming perception[J]. Journal of Signal Processing, 2017, 33(12): 1652–1656. doi: 10.16798/j.issn.1003-0530.2017.12.018 [13] ZHANG Yang, WEI Yinsheng, and YU Lei. Interrupted sampling repeater jamming recognition and suppression based on phase-coded signal processing[J]. Signal Processing, 2022, 198: 108596. doi: 10.1016/j.sigpro.2022.108596 [14] ZHOU Chao, LIU Quanhua, and CHEN Xinliang. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer[J]. IET Radar, Sonar & Navigation, 2018, 12(1): 56–63. doi: 10.1049/iet-rsn.2017.0114 [15] 杨小鹏, 韩博文, 吴旭晨, 等. 基于短时分数阶傅里叶变换的间歇采样转发干扰辨识方法[J]. 信号处理, 2019, 35(6): 1002–1010. doi: 10.16798/j.issn.1003-0530.2019.06.010YANG Xiaopeng, HAN Bowen, WU Xuchen, et al. Interrupted sampling repeater jamming identification method based on Short-time fractional Fourier transform[J]. Journal of Signal Processing, 2019, 35(6): 1002–1010. doi: 10.16798/j.issn.1003-0530.2019.06.010 [16] 周畅, 范甘霖, 汤子跃, 等. 间歇采样转发干扰的关键参数估计[J]. 太赫兹科学与电子信息学报, 2019, 17(5): 782–787. doi: 10.11805/TKYDA201905.0782ZHOU Chang, FAN Ganlin, TANG Ziyue, et al. Parameter estimation of intermittent sampling repeater jamming[J]. Journal of Terahertz Science and Electronic Information Technology, 2019, 17(5): 782–787. doi: 10.11805/TKYDA201905.0782 [17] 周超, 刘泉华, 曾涛. DRFM间歇采样转发式干扰辨识算法研究[J]. 信号处理, 2017, 33(7): 911–917. doi: 10.16798/j.issn.1003-0530.2017.07.002ZHOU Chao, LIU Quanhua, and ZENG Tao. Research on DRFM repeater jamming recognition[J]. Journal of Signal Processing, 2017, 33(7): 911–917. doi: 10.16798/j.issn.1003-0530.2017.07.002 [18] 尚东东, 张劲东, 胡婉婉, 等. 基于ADMM的间歇采样转发式干扰的参数估计[J]. 雷达科学与技术, 2021, 19(4): 417–422,429. doi: 10.3969/j.issn.1672-2337.2021.04.008SHANG Dongdong, ZHANG Jindong, HU Wanwan, et al. Parameter estimation of interrupted sampling repeater jamming based on ADMM[J]. Radar Science and Technology, 2021, 19(4): 417–422,429. doi: 10.3969/j.issn.1672-2337.2021.04.008 [19] MENG Yunyun, YU Lei, WEI Yinsheng, et al. A novel parameter estimation method of interrupted sampling repeater jamming[C]. 2019 IEEE International Conference on Signal, Information and Data Processing, Chongqing, China, 2019: 1–5. [20] ZHOU Chao, SHI Fuqiang, and LIU Quanhua. Research on parameters estimation and suppression for C&I Jamming[C]. 2016 CIE International Conference on Radar, Guangzhou, China, 2016: 1–4. [21] WU Chuanzhang, CHEN Baixiao, YANG Minglei, et al. A method of parameter estimation and suppression for smeared spectrum jamming[C]. 2019 5th International Conference on Frontiers of Signal Processing, Marseille, France, 2019: 149–153. [22] 刘国满, 聂旭娜. 一种基于卷积神经网络的雷达干扰识别算法[J]. 北京理工大学学报, 2021, 41(9): 990–998. doi: 10.15918/j.tbit1001-0645.2020.220LIU Guoman and NIE Xuna. A radar jamming recognition algorithm based on convolutional neural network[J]. Transactions of Beijing Institute of Technology, 2021, 41(9): 990–998. doi: 10.15918/j.tbit1001-0645.2020.220 [23] QU Qizhe, WEI Shunjun, LIU Shan, et al. JRNet: Jamming recognition networks for radar compound suppression jamming signals[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15035–15045. doi: 10.1109/TVT.2020.3032197 [24] ZHANG Haoyu, YU Lei, CHEN Yushi, et al. Fast complex-valued CNN for radar jamming signal recognition[J]. Remote Sensing, 2021, 13(15): 2867. doi: 10.3390/rs13152867 [25] QIN Ying, YANG Jing, ZHU Mengtao, et al. Fast recognition of pull-off jamming using LSTM[C]. 2019 IEEE International Conference on Signal, Information and Data Processing, Chongqing, China, 2019: 1–5. [26] SHAO Guangqing, CHEN Yushi, and WEI Yinsheng. Deep fusion for radar jamming signal classification based on CNN[J]. IEEE Access, 2020, 8: 117236–117244. doi: 10.1109/ACCESS.2020.3004188 [27] KONG Yukai, WANG Xiang, WU Changxin, et al. Active deception jamming recognition in the presence of extended target[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4024905. doi: 10.1109/LGRS.2022.3184997 [28] LV Qinzhe, QUAN Yinghui, FENG Wei, et al. Radar deception jamming recognition based on weighted ensemble CNN with transfer learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5107511. doi: 10.1109/TGRS.2021.3129645 [29] SHAO Guangqing, CHEN Yushi, and WEI Yinsheng. Convolutional neural network-based radar jamming signal classification with sufficient and limited samples[J]. IEEE Access, 2020, 8: 80588–80598. doi: 10.1109/ACCESS.2020.2990629 [30] HAYKIN S, XUE Yanbo, and DAVIDSON T N. Optimal waveform design for cognitive radar[C]. 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 2008: 3–7. [31] 吴悦, 张劲东, 张杰, 等. 认知雷达干扰和旁瓣均衡抑制的波形设计[J]. 雷达科学与技术, 2018, 16(1): 61–67. doi: 10.3969/j.issn.1672-2337.2018.01.010WU Yue, ZHANG Jindong, ZHANG Jie, et al. Waveform design for equally suppressing interference and sidelobes in cognitive radar[J]. Radar Science and Technology, 2018, 16(1): 61–67. doi: 10.3969/j.issn.1672-2337.2018.01.010 [32] 张杰, 陈婉迎, 吴悦. 认知雷达二维自适应抗干扰捷变波形设计[J]. 雷达科学与技术, 2019, 17(4): 415–420, 425. doi: 10.3969/j.issn.1672-2337.2019.04.010ZHANG Jie, CHEN Wanying, and WU Yue. Adaptive anti-jamming design for two-dimensional waveform agility in cognitive radar system[J]. Radar Science and Technology, 2019, 17(4): 415–420, 425. doi: 10.3969/j.issn.1672-2337.2019.04.010 [33] SOLTANALIAN M, TANG Bo, LI Jian, et al. Joint design of the receive filter and transmit sequence for active sensing[J]. IEEE Signal Processing Letters, 2013, 20(5): 423–426. doi: 10.1109/LSP.2013.2250279 [34] 蒋孟燃, 李伟, 兰星, 等. 干扰条件下基于MMSE准则的弹载雷达认知波形优化[J]. 火力与指挥控制, 2018, 43(4): 158–164. doi: 10.3969/j.issn.1002-0640.2018.04.035JIANG Mengran, LI Wei, LAN Xing, et al. Cognitive waveform optimization for missile-borne radar using MMSE criterion[J]. Fire Control &Command Control, 2018, 43(4): 158–164. doi: 10.3969/j.issn.1002-0640.2018.04.035 [35] TANG Bo, TUCK J, and STOICA P. Polyphase waveform design for MIMO radar space time adaptive processing[J]. IEEE Transactions on Signal Processing, 2020, 68: 2143–2154. doi: 10.1109/TSP.2020.2983833 [36] ZHANG Jindong, ZHU Daiyin, and ZHANG Gong. New antivelocity deception jamming technique using pulses with adaptive initial phases[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1290–1300. doi: 10.1109/TAES.2013.6494414 [37] 吴健. 基于波形分集的雷达抗有源欺骗干扰技术研究[D]. [硕士论文], 电子科技大学, 2015.WU Jian. Research of technology against radar active deception jamming based on waveform diversity[D]. [Master dissertation], University of Electronic Science and Technology of China, 2015. [38] XIONG Wei, WANG Xinhai, and ZHANG Gong. Cognitive waveform design for anti-velocity deception jamming with adaptive initial phases[C]. 2016 IEEE Radar Conference, Philadelphia, USA, 2016: 1–5. [39] 卜祎. 机载雷达认知抗干扰波形设计与处理方法[D]. [硕士论文], 电子科技大学, 2021.BU Yi. Design and processing of cognitive anti-jamming waveforms for airborne radar[D]. [Master dissertation], University of Electronic Science and Technology of China, 2021. [40] 葛萌萌. 认知雷达多维联合抗主瓣干扰研究[D]. [博士论文], 电子科技大学, 2021.GE Mengmeng. Cognitive radar mainlobe jamming suppression methods via multidimensional signal design and processing[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2021. [41] FENG Xiang, SONG Yangchun, ZHOU Zhiquan, et al. Designing unimodular waveform with low range sidelobes and stopband for cognitive radar via relaxed alternating projection[J]. International Journal of Antennas and Propagation, 2016: 6280508. doi: 10.1155/2016/6280508 [42] SOUMEKH M. SAR-ECCM using phase-perturbed LFM chirp signals and DRFM repeat jammer penalization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 191–205. doi: 10.1109/TAES.2006.1603414 [43] AKHTAR J. An ECCM scheme for orthogonal independent range-focusing of real and false targets[C]. 2007 IEEE Radar Conference, Waltham, USA, 2007: 846–849. [44] AKHTAR J. Orthogonal block coded ECCM schemes against repeat radar jammers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 1218–1226. doi: 10.1109/TAES.2009.5259195 [45] YANG Ya, CUI Guolong, WU Jian, et al. Optimized phase-coded waveforms design against range repeat jamming[C]. 2015 IEEE Radar Conference, Arlington, USA, 2015: 395–399. [46] BU Yi, YU Xianxiang, YANG Jing, et al. A new approach for design of constant modulus discrete phase radar waveform with low WISL[J]. Signal Processing, 2021, 187: 108145. doi: 10.1016/j.sigpro.2021.108145 [47] 张梅仓, 王磊. 火控雷达认知抗干扰技术研究[J]. 现代雷达, 2016, 38(12): 91–94. doi: 10.16592/j.cnki.1004-7859.2016.12.019ZHANG Meicang and WANG Lei. A study on the technology of cognitive anti-jamming for fire control radar[J]. Modern Radar, 2016, 38(12): 91–94. doi: 10.16592/j.cnki.1004-7859.2016.12.019 [48] 吴悦. 基于自适应捷变波形的认知雷达干扰对抗技术[D]. [硕士论文], 南京航空航天大学, 2018.WU Yue. Anti-jamming technology of cognitive radar based on adaptive agile waveform[D]. [Master dissertation], Nanjing University of Aeronautics and Astronautics, 2018. [49] 崔国龙, 樊涛, 孔昱凯, 等. 机载雷达脉间波形参数伪随机跳变技术[J]. 雷达学报, 2022, 11(2): 213–226. doi: 10.12000/JR21189CUI Guolong, FAN Tao, KONG Yukai, et al. Pseudo-random agility technology for interpulse waveform parameters in airborne radar[J]. Journal of Radars, 2022, 11(2): 213–226. doi: 10.12000/JR21189 [50] 周超, 刘泉华, 胡程. 间歇采样转发式干扰的时频域辨识与抑制[J]. 雷达学报, 2019, 8(1): 100–106. doi: 10.12000/JR18080ZHOU Chao, LIU Quanhua, and HU Cheng. Time-frequency analysis techniques for recognition and suppression of interrupted sampling repeater jamming[J]. Journal of Radars, 2019, 8(1): 100–106. doi: 10.12000/JR18080 [51] ZHOU Kai, LI Dexin, SU Yi, et al. Joint design of transmit waveform and mismatch filter in the presence of interrupted sampling repeater jamming[J]. IEEE Signal Processing Letters, 2020, 27: 1610–1614. doi: 10.1109/LSP.2020.3021667 [52] 何金阳, 程子扬, 何子述. 抗间歇采样转发干扰的认知恒模波形设计方法[J]. 系统工程与电子技术, 2021, 43(9): 2448–2456. doi: 10.12305/j.issn.1001-506X.2021.09.10HE Jinyang, CHENG Ziyang, and HE Zishu. Cognitive constant modulus waveform design method against interrupted sampling repeater jamming[J]. Systems Engineering and Electronics, 2021, 43(9): 2448–2456. doi: 10.12305/j.issn.1001-506X.2021.09.10 [53] GE Mengmeng, YU Xianxiang, YAN Zhengxin, et al. Joint cognitive optimization of transmit waveform and receive filter against deceptive interference[J]. Signal Processing, 2021, 185: 108084. doi: 10.1016/j.sigpro.2021.108084 [54] 周畅, 汤子跃, 余方利, 等. 基于脉内正交的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06ZHOU Chang, TANG Ziyue, YU Fangli, et al. Anti intermittent sampling repeater jamming method based on intrapulse orthogonality[J]. Systems Engineering and Electronics, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06 [55] 吴少鹏, 袁越, 涂刚毅. 间歇采样干扰识别的抗欺骗干扰波形设计[J]. 现代防御技术, 2018, 46(2): 1–5, 81. doi: 10.3969/j.issn.1009-086x.2018.02.001WU Shaopeng, YUAN Yue, and TU Gangyi. Design of anti deception jamming waveform for intermittent sampling interference identification[J]. Modern Defence Technology, 2018, 46(2): 1–5, 81. doi: 10.3969/j.issn.1009-086x.2018.02.001 [56] 谭怀英, 张鹏, 贺青, 等. 雷达参数级智能化抗干扰研究及应用[J]. 现代雷达, 2021, 43(11): 15–22. doi: 10.16592/j.cnki.1004-7859.2021.11.003TAN Huaiying, ZHANG Peng, HE Qing, et al. Research and application on radar parametric level intelligent anti-jamming[J]. Modern Radar, 2021, 43(11): 15–22. doi: 10.16592/j.cnki.1004-7859.2021.11.003 [57] WEI Zhenhua, LIU Zhen, PENG Bo, et al. ECCM scheme against interrupted sampling repeater jammer based on parameter-adjusted waveform design[J]. Sensors, 2018, 18(4): 1141. doi: 10.3390/s18041141 [58] 刘智星, 杜思予, 吴耀君, 等. 脉间-脉内捷变频雷达抗间歇采样干扰方法[J]. 雷达学报, 2022, 11(2): 301–312. doi: 10.12000/JR22001LIU Zhixing, DU Siyu, WU Yaojun, et al. Anti-interrupted sampling repeater jamming method for interpulse and intrapulse frequency-agile radar[J]. Journal of Radars, 2022, 11(2): 301–312. doi: 10.12000/JR22001 [59] 杜思予, 刘智星, 吴耀君, 等. 频率捷变波形联合时频滤波器抗间歇采样转发干扰[J/OL]. 系统工程与电子技术, http://kns.cnki.net/kcms/detail/11.2422.TN.20220611.1458.012.html, 2022.DU Siyu, LIU Zhixing, WU Yaojun, et al. Frequency agility waveform combined with time-frequency filter to suppress interrupted-sampling repeater jamming[J/OL]. Systems Engineering and Electronics, http://kns.cnki.net/kcms/detail/11.2422.TN.20220611.1458.012.html, 2022. [60] 全英汇, 陈侠达, 阮锋, 等. 一种捷变频联合Hough变换的抗密集假目标干扰算法[J]. 电子与信息学报, 2019, 41(11): 2639–2645. doi: 10.11999/JEIT190010QUAN Yinghui, CHEN Xiada, RUAN Feng, et al. An anti-dense false target jamming algorithm based on agile frequency joint Hough transform[J]. Journal of Electronics & Information Technology, 2019, 41(11): 2639–2645. doi: 10.11999/JEIT190010 [61] 方文, 全英汇, 沙明辉, 等. 捷变频联合波形熵的密集假目标干扰抑制算法[J]. 系统工程与电子技术, 2021, 43(6): 1506–1514. doi: 10.12305/j.issn.1001-506X.2021.06.07FANG Wen, QUAN Yinghui, SHA Minghui, et al. Dense false targets jamming suppression algorithm based on frequency agility and waveform entropy[J]. Systems Engineering and Electronics, 2021, 43(6): 1506–1514. doi: 10.12305/j.issn.1001-506X.2021.06.07 [62] LU Shuping, CUI Guolong, YU Xianxiang, et al. Cognitive radar waveform design against signal-dependent modulated jamming[J]. Progress in Electromagnetics Research B, 2018, 80: 59–77. doi: 10.2528/PIERB18010805 [63] 王福来, 庞晨, 殷加鹏, 等. 一种多普勒容忍的抗间歇采样转发干扰恒模互补波形和接收滤波器联合设计方法[J]. 雷达学报, 2022, 11(2): 278–288. doi: 10.12000/JR22020WANG Fulai, PANG Chen, YIN Jiapeng, et al. Joint design of Doppler-tolerant complementary sequences and receiving filters against interrupted sampling repeater jamming[J]. Journal of Radars, 2022, 11(2): 278–288. doi: 10.12000/JR22020 [64] ANGELETTI P, BERRETTI L, MADDIO S, et al. Phase-only synthesis for large planar arrays via Zernike polynomials and invasive weed optimization[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(3): 1954–1964. doi: 10.1109/TAP.2021.3119113 [65] 刘肖萌, 高文军, 邓云凯, 等. 基于投影矩阵法的阵列天线波束形成方法[J]. 雷达学报, 2012, 1(1): 50–57. doi: 10.3724/SP.J.1300.2012.20012LIU Xiaomeng, GAO Wenjun, DENG Yunkai, et al. Beam synthesis technique for array antenna based on projection matrix algorithm[J]. Journal of Radars, 2012, 1(1): 50–57. doi: 10.3724/SP.J.1300.2012.20012 [66] ASLAN Y, PUSKELY J, ROEDERER A, et al. Phase-only control of peak sidelobe level and pattern nulls using iterative phase perturbations[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(10): 2081–2085. doi: 10.1109/LAWP.2019.2937682 [67] ZHAO Zhonghui, ZHAO Huiling, WANG Zhaoping, et al. Radial basis function neural network optimal modeling for phase-only array pattern nulling[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(11): 7971–7975. doi: 10.1109/TAP.2021.3083787 [68] ZHANG Xuan, WANG Xiangrong, and SO H C. Linear arbitrary array pattern synthesis with shape constraints and excitation range control[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(6): 1018–1022. doi: 10.1109/LAWP.2021.3069743 [69] KAJENSKI P J. Phase only antenna pattern notching via a semidefinite programming relaxation[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(5): 2562–2565. doi: 10.1109/TAP.2012.2189709 [70] FUCHS B. Application of convex relaxation to array synthesis problems[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(2): 634–640. doi: 10.1109/TAP.2013.2290797 [71] LIANG Junli, FAN Xuhui, FAN Wen, et al. Phase-only pattern synthesis for linear antenna arrays[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 3232–3235. doi: 10.1109/LAWP.2017.2771380 [72] GEMECHU A Y, CUI Guolong, YU Xianxiang, et al. Beampattern synthesis with sidelobe control and applications[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(1): 297–310. doi: 10.1109/TAP.2019.2938730 [73] DOLPH C L. A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level[J]. Proceedings of the IRE, 1946, 34(6): 335–348. doi: 10.1109/JRPROC.1946.225956 [74] TAYLOR T T. Design of line-source antennas for narrow beamwidth and low side lobes[J]. Transactions of the IRE Professional Group on Antennas and Propagation, 1955, 3(1): 16–28. doi: 10.1109/TPGAP.1955.5720407 [75] DE ABREU G T and KOHNO R. A modified Dolph-Chebyshev approach for the synthesis of low sidelobe beampatterns with adjustable beamwidth[J]. IEEE Transactions on Antennas and Propagation, 2003, 51(10): 3014–3017. doi: 10.1109/TAP.2003.817989 [76] SAHIDULLAH M and SAHA G. A novel windowing technique for efficient computation of MFCC for speaker recognition[J]. IEEE Signal Processing Letters, 2013, 20(2): 149–152. doi: 10.1109/LSP.2012.2235067 [77] KULKARNI R G. Polynomial windows with fast decaying sidelobes for narrow-band signals[J]. Signal Processing, 2003, 83(6): 1145–1149. doi: 10.1016/S0165-1684(03)00019-7 [78] OKARMA K. Polynomial windows with low sidelobes’ level[J]. Signal Processing, 2007, 87(4): 782–788. doi: 10.1016/j.sigpro.2006.09.007 [79] LIM Y C, SARAMÄKI T, DINIZ P S R, et al. Fast convergence method for scaling window sidelobe magnitude[J]. IEEE Signal Processing Letters, 2021, 28: 2078–2081. doi: 10.1109/LSP.2021.3116517 [80] LIM Y C, SARAMÄKI T, DINIZ P S R, et al. A method for scaling window sidelobe magnitude[J]. IEEE Signal Processing Letters, 2021, 28: 1056–1059. doi: 10.1109/LSP.2021.3079847 [81] CHEN Kesong, YUN Xiaohua, HE Zishu, et al. Synthesis of sparse planar arrays using modified real genetic algorithm[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(4): 1067–1073. doi: 10.1109/TAP.2007.893375 [82] MURINO V, TRUCCO A, and REGAZZONI C S. Synthesis of unequally spaced arrays by simulated annealing[J]. IEEE Transactions on Signal Processing, 1996, 44(1): 119–122. doi: 10.1109/78.482017 [83] BOERINGER D W and WERNER D H. Particle swarm optimization versus genetic algorithms for phased array synthesis[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(3): 771–779. doi: 10.1109/TAP.2004.825102 [84] REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853–863. doi: 10.1109/TAES.1974.307893 [85] ZHANG Xuejing, HE Zishu, LIAO Bin, et al. A2RC: An accurate array response control algorithm for pattern synthesis[J]. IEEE Transactions on Signal Processing, 2017, 65(7): 1810–1824. doi: 10.1109/TSP.2017.2649487 [86] ZHANG Xuejing, HE Zishu, LIAO Bin, et al. Pattern synthesis with multipoint accurate array response control[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(8): 4075–4088. doi: 10.1109/TAP.2017.2718582 [87] ZHANG Xuejing, HE Zishu, LIAO Bin, et al. Pattern synthesis for arbitrary arrays via weight vector orthogonal decomposition[J]. IEEE Transactions on Signal Processing, 2018, 66(5): 1286–1299. doi: 10.1109/TSP.2017.2787143 [88] ZHANG Xuejing, HE Zishu, LIAO Bin, et al. Pattern synthesis via oblique projection-based multipoint array response control[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(7): 4602–4616. doi: 10.1109/TAP.2019.2911317 [89] ZHOU P Y and INGRAM M A. Pattern synthesis for arbitrary arrays using an adaptive array method[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(5): 862–869. doi: 10.1109/8.774142 [90] SHI Zhan and FENG Zhenghe. A new array pattern synthesis algorithm using the two-step least-squares method[J]. IEEE Signal Processing Letters, 2005, 12(3): 250–253. doi: 10.1109/LSP.2004.842282 [91] WANG Fan, BALAKRISHNAN V, ZHOU P Y, et al. Optimal array pattern synthesis using semidefinite programming[J]. IEEE Transactions on Signal Processing, 2003, 51(5): 1172–1183. doi: 10.1109/TSP.2003.810308 [92] CAO Pan, THOMPSON J S, and HAAS H. Constant modulus shaped beam synthesis via convex relaxation[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 617–620. doi: 10.1109/LAWP.2016.2594141 [93] LIANG Junli, FAN Xuhui, SO H C, et al. Array beampattern synthesis without specifying lobe level masks[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(6): 4526–4539. doi: 10.1109/TAP.2020.2972331 [94] ZHANG Xuejing, HE Zishu, ZHANG Xuepan, et al. High-performance beampattern synthesis via linear fractional semidefinite relaxation and quasi-convex optimization[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(7): 3421–3431. doi: 10.1109/TAP.2018.2835310 [95] LU Qinghui, CUI Guolong, LIU Ruitao, et al. Beampattern synthesis via first-order iterative convex approximation[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(8): 1493–1497. doi: 10.1109/LAWP.2021.3088472 [96] LIU Ruitao, ZHANG Wei, YU Xianxiang, et al. Transmit-receive beamforming for distributed phased-MIMO radar system[J]. IEEE Transactions on Vehicular Technology, 2022, 71(2): 1439–1453. doi: 10.1109/TVT.2021.3133596 [97] CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408–1418. doi: 10.1109/PROC.1969.7278 [98] WANG Xiangrong, GRECO M S, and GINI F. Adaptive sparse array beamformer design by regularized complementary antenna switching[J]. IEEE Transactions on Signal Processing, 2021, 69: 2302–2315. doi: 10.1109/TSP.2021.3064183 [99] COX H, ZESKIND R, and OWEN M. Robust adaptive beamforming[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35(10): 1365–1376. doi: 10.1109/TASSP.1987.1165054 [100] CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1988, 24(4): 397–401. doi: 10.1109/7.7181 [101] FELDMAN D D and GRIFFITHS L J. A projection approach for robust adaptive beamforming[J]. IEEE Transactions on Signal Processing, 1994, 42(4): 867–876. doi: 10.1109/78.285650 [102] CHANG L and YEH C C. Performance of DMI and eigenspace-based beamformers[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(11): 1336–1347. doi: 10.1109/8.202711 [103] VOROBYOV S A, GERSHMAN A B, and LUO Zhiquan. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 313–324. doi: 10.1109/TSP.2002.806865 [104] LI Jian, STOICA P, and WANG Zhisong. On robust capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1702–1715. doi: 10.1109/TSP.2003.812831 [105] SHAHBAZPANAHI S, GERSHMAN A B, LUO Zhiquan, et al. Robust adaptive beamforming for general-rank signal models[J]. IEEE Transactions on Signal Processing, 2003, 51(9): 2257–2269. doi: 10.1109/TSP.2003.815395 [106] LORENZ R G and BOYD S P. Robust minimum variance beamforming[J]. IEEE Transactions on Signal Processing, 2005, 53(5): 1684–1696. doi: 10.1109/TSP.2005.845436 [107] LIAO Bin, GUO Chongtao, HUANG Lei, et al. Robust adaptive beamforming with precise main beam control[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 345–356. doi: 10.1109/TAES.2017.2650578 [108] LIAO Bin, TSUI K M, and CHAN S C. Robust beamforming with magnitude response constraints using iterative second-order cone programming[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(9): 3477–3482. doi: 10.1109/TAP.2011.2161445 [109] LIAO Bin and CHAN S C. Adaptive beamforming for uniform linear arrays with unknown mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2012, 11: 464–467. doi: 10.1109/LAWP.2012.2196017 [110] DU Dongping and TANG Bin. Noise FM jamming suppression via logarithm transform[C]. 2008 International Conference on Communications, Circuits and Systems, Xiamen, China, 2008: 957–959. [111] 杜东平, 唐斌. 基于频域对消的噪声调幅干扰抑制算法[J]. 电子与信息学报, 2007, 29(3): 557–559. doi: 10.3724/SP.J.1146.2005.00999DU Dongping and TANG Bin. A high performance algorithm of noise amplitude modulation interference suppression based on frequency domain cancellation[J]. Journal of Electronics &Information Technology, 2007, 29(3): 557–559. doi: 10.3724/SP.J.1146.2005.00999 [112] 张帅. 分布式雷达抗干扰与目标检测方法研究[D]. [硕士论文], 电子科技大学, 2017.ZHANG Shuai. Research of distributed radar technology against jamming and target detection[D]. [Master dissertation], University of Electronic Science and Technology of China, 2017. [113] CUI Guolong, YU Xianxiang, YUAN Ye, et al. Range jamming suppression with a coupled sequential estimation algorithm[J]. IET Radar, Sonar & Navigation, 2018, 12(3): 341–347. doi: 10.1049/iet-rsn.2017.0365 [114] CUI Guolong, JI Hongmin, CAROTENUTO V, et al. An adaptive sequential estimation algorithm for velocity jamming suppression[J]. Signal Processing, 2017, 134: 70–75. doi: 10.1016/j.sigpro.2016.11.012 [115] ZHANG Shuai, YANG Ya, CUI Guolong, et al. Range-velocity jamming suppression algorithm based on adaptive iterative filtering[C]. 2016 IEEE Radar Conference, Philadelphia, USA, 2016: 1–6. [116] NATHANSON F E. Adaptive circular polarization[C]. International Radar Conference, Arlington, USA, 1975: 221–225. [117] 施龙飞. 雷达极化抗干扰技术研究[D]. [博士论文], 国防科学技术大学, 2007.SHI Longfei. Study on the suppression of interference with radar polarization information[D]. [Ph. D. dissertation], National University of Defense Technology, 2007. [118] 王雪松. 宽带极化信息处理的研究[D]. [博士论文], 国防科学技术大学, 1999.WANG Xuesong. Study on wideband polarization information processing[D]. [Ph. D. dissertation], National University of Defense Technology, 1999. [119] XIONG Wei, ZHANG Gong, and LIU Wenbo. Efficient filter design against interrupted sampling repeater jamming for wideband radar[J]. EURASIP Journal on Advances in Signal Processing, 2017, 2017(1): 9. doi: 10.1186/s13634-017-0446-3 [120] CHEN Jian, WU Wenzhen, XU Shiyou, et al. Band pass filter design against interrupted-sampling repeater jamming based on time-frequency analysis[J]. IET Radar, Sonar & Navigation, 2019, 13(10): 1646–1654. doi: 10.1049/iet-rsn.2018.5658 [121] 孙正阳, 董玫, 陈伯孝. 时频分析联合带通滤波抑制间歇采样转发干扰[J]. 西安电子科技大学学报, 2021, 48(2): 139–146, 180. doi: 10.19665/j.issn1001-2400.2021.02.018SUN Zhengyang, DONG Mei, and CHEN Baixiao. Interrupted sampling repeater jamming suppression based on time-frequency analysis and band-pass filtering[J]. Journal of Xidian University, 2021, 48(2): 139–146, 180. doi: 10.19665/j.issn1001-2400.2021.02.018 [122] ELGAMEL S A and SORAGHAN J J. Using EMD-FrFT filtering to mitigate very high power interference in chirp tracking radars[J]. IEEE Signal Processing Letters, 2011, 18(4): 263–266. doi: 10.1109/lsp.2011.2115239 [123] BRENNAN L E and REED I S. Theory of adaptive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(2): 237–252. doi: 10.1109/TAES.1973.309792 [124] TANG Bo, LI Jun, ZHANG Yu, et al. Design of MIMO radar waveform covariance matrix for Clutter and Jamming suppression based on space time adaptive processing[J]. Signal Processing, 2016, 121: 60–69. doi: 10.1016/j.sigpro.2015.10.033 [125] BOLHASANI M, MEHRSHAHI E, and GHORASHI S A. Waveform covariance matrix design for robust signal-dependent interference suppression in colocated MIMO radars[J]. Signal Processing, 2018, 152: 311–319. doi: 10.1016/j.sigpro.2018.06.007 [126] XU Jingwei, LIAO Guisheng, ZHU Shengqi, et al. Deceptive jamming suppression with frequency diverse MIMO radar[J]. Signal Processing, 2015, 113: 9–17. doi: 10.1016/j.sigpro.2015.01.014 [127] WEN Cai, PENG Jinye, ZHOU Yan, et al. Enhanced three-dimensional joint domain localized STAP for airborne FDA-MIMO radar under dense false-target jamming scenario[J]. IEEE Sensors Journal, 2018, 18(10): 4154–4166. doi: 10.1109/jsen.2018.2820905 [128] 徐振海, 王雪松, 肖顺平, 等. 极化敏感阵列滤波性能分析: 完全极化情形[J]. 电子学报, 2004, 32(8): 1310–1313. doi: 10.3321/j.issn:0372-2112.2004.08.019XU Zhenhai, WANG Xuesong, XIAO Shunping, et al. Filtering performance of polarization sensitive array: Completely polarized case[J]. Acta Electronica Sinica, 2004, 32(8): 1310–1313. doi: 10.3321/j.issn:0372-2112.2004.08.019 [129] 徐振海, 王雪松, 肖顺平, 等. 极化敏感阵列滤波性能分析: 相关干扰情形[J]. 通信学报, 2004, 25(10): 8–15. doi: 10.3321/j.issn:1000-436X.2004.10.002XU Zhenhai, WANG Xuesong, XIAO Shunping, et al. Filtering performance of polarization sensitive array: Correlated interference case[J]. Journal of China Institute of Communications, 2004, 25(10): 8–15. doi: 10.3321/j.issn:1000-436X.2004.10.002 [130] MA Jiazhi, SHI Longfei, LI Yongzhen, et al. Angle estimation of extended targets in main-lobe interference with polarization filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 169–189. doi: 10.1109/TAES.2017.2649783 [131] 唐佳, 于海洋, 杨福荣. 一种新的基于空极联合估计抗干扰方法[J]. 电子信息对抗技术, 2021, 36(6): 18–22. doi: 10.3969/j.issn.1674-2230.2021.06.004TANG Jia, YU Haiyang, and YANG Furong. A new algorithm of anti-jamming based on space-polar joint estimation[J]. Electronic Information Warfare Technology, 2021, 36(6): 18–22. doi: 10.3969/j.issn.1674-2230.2021.06.004 [132] 宁立跃. 基于空-极化域联合的主瓣干扰抑制算法研究[D]. [硕士论文], 北京理工大学, 2018.NING Liyue. Research on main-lobe interference suppression algorithm based on joint space and polarization domain[D]. [Master dissertation], Beijing Institute of Technology, 2018. [133] HUANG Gaoming, YANG Luxi, and SU Guoqing. Blind source separation used for radar anti-jamming[C]. 2003 International Conference on Neural Networks and Signal Processing, Nanjing, China, 2003: 1382–1385. [134] 罗双才, 唐斌. 一种基于盲分离的欺骗干扰抑制算法[J]. 电子与信息学报, 2011, 33(12): 2801–2806. doi: 10.3724/SP.J.1146.2011.00380LUO Shuangcai and TANG Bin. An algorithm of deception jamming suppression based on blind signal separation[J]. Journal of Electronics &Information Technology, 2011, 33(12): 2801–2806. doi: 10.3724/SP.J.1146.2011.00380 [135] 黄高明, 杨绿溪, 何振亚. 一种基于盲源分离的雷达抗干扰技术[J]. 电路与系统学报, 2004, 9(6): 94–99. doi: 10.3969/j.issn.1007-0249.2004.06.022HUANG Gaoming, YANG Luxi, and HE Zhenya. A radar anti-jamming technology based on blind source separation[J]. Journal of Circuits and Systems, 2004, 9(6): 94–99. doi: 10.3969/j.issn.1007-0249.2004.06.022 [136] 王建明, 伍光新, 周伟光. 盲源分离在雷达抗主瓣干扰中的应用研究[J]. 现代雷达, 2010, 32(10): 46–49. doi: 10.3969/j.issn.1004-7859.2010.10.011WANG Jianming, WU Guangxin, and ZHOU Weiguang. A study on radar mainlobe jamming suppression based on blind source separation algorithm[J]. Modern Radar, 2010, 32(10): 46–49. doi: 10.3969/j.issn.1004-7859.2010.10.011 [137] 王文涛, 张剑云, 刘兴华, 等. JADE盲源分离算法应用于雷达抗主瓣干扰技术[J]. 火力与指挥控制, 2015, 40(9): 104–108. doi: 10.3969/j.issn.1002-0640.2015.09.026WANG Wentao, ZHANG Jianyun, LIU Xinghua, et al. Radar anti-mainlobe-jamming based on blind source separation algorithm of JADE[J]. Fire Control &Command Control, 2015, 40(9): 104–108. doi: 10.3969/j.issn.1002-0640.2015.09.026 [138] 王文涛, 张剑云, 李小波, 等. Fast ICA应用于雷达抗主瓣干扰算法研究[J]. 信号处理, 2015, 31(4): 497–503. doi: 10.3969/j.issn.1003-0530.2015.04.016WANG Wentao, ZHANG Jianyun, LI Xiaobo, et al. A study on radar mainlobe jamming suppression algorithm based on Fast ICA[J]. Journal of Signal Processing, 2015, 31(4): 497–503. doi: 10.3969/j.issn.1003-0530.2015.04.016 [139] 周青松, 王文涛, 王珽, 等. 盲分离算法和FRFT联合抗雷达主瓣干扰技术研究[J]. 信号处理, 2015, 31(8): 1004–1011. doi: 10.3969/j.issn.1003-0530.2015.08.017ZHOU Qingsong, WANG Wentao, WANG Ting, et al. A study on radar mainlobe jamming suppression technique based on method of BSS-FRFT union[J]. Journal of Signal Processing, 2015, 31(8): 1004–1011. doi: 10.3969/j.issn.1003-0530.2015.08.017 [140] LUO Shuangcai, XIONG Ying, CHENG Hao, et al. An algorithm of radar deception jamming suppression based on blind signal separation[C]. 2011 International Conference on Computational Problem-Solving, Chengdu, China, 2011: 167–170. [141] ZHOU Bilei, LI Rongfeng, LIU Weijian, et al. A BSS-based space-time multi-channel algorithm for complex-jamming suppression[J]. Digital Signal Processing, 2019, 87: 86–103. doi: 10.1016/j.dsp.2019.01.007 [142] 高霞, 全英汇, 李亚超, 等. 基于BSS的FDA-MIMO雷达主瓣欺骗式干扰抑制方法[J]. 系统工程与电子技术, 2020, 42(9): 1927–1934. doi: 10.3969/j.issn.1001-506X.2020.09.07GAO Xia, QUAN Yinghui, LI Yachao, et al. Main-lobe deceptive jamming suppression with FDA-MIMO radar based on BSS[J]. Systems Engineering and Electronics, 2020, 42(9): 1927–1934. doi: 10.3969/j.issn.1001-506X.2020.09.07 [143] 葛萌萌, 崔国龙, 孔令讲, 等. 分布式雷达盲源分离干扰抑制算法[J]. 信号处理, 2017, 33(12): 1562–1570. doi: 10.16798/j.issn.1003-0530.2017.12.006GE Mengmeng, CUI Guolong, KONG Lingjiang, et al. Jamming suppression based on blind source separation in distributed radars[J]. Journal of Signal Processing, 2017, 33(12): 1562–1570. doi: 10.16798/j.issn.1003-0530.2017.12.006 [144] GE Mengmeng, CUI Guolong, and KONG Lingjiang. Mainlobe jamming suppression for distributed radar via joint blind source separation[J]. IET Radar, Sonar & Navigation, 2019, 13(7): 1189–1199. doi: 10.1049/iet-rsn.2018.5434 [145] GE Mengmeng, CUI Guolong, SHI Qiao, et al. Mainlobe jamming suppression based on joint blind source separation for distributed radar[C]. 2019 IEEE Radar Conference, Boston, USA, 2019: 1–5. [146] DE LIEVEN L and CASTAING J. Blind identification of underdetermined mixtures by simultaneous matrix diagonalization[J]. IEEE Transactions on Signal Processing, 2008, 56(3): 1096–1105. doi: 10.1109/TSP.2007.908929 [147] 张延良, 楼顺天, 张伟涛. 欠定盲源分离混合矩阵估计的张量分解方法[J]. 系统工程与电子技术, 2011, 33(8): 1703–1706. doi: 10.3969/j.issn.1001-506X.2011.08.05ZHANG Yanliang, LOU Shuntian, and ZHANG Weitao. Estimation of underdetermined mixture matrix in blind source separation based on tensor decomposition[J]. Systems Engineering and Electronics, 2011, 33(8): 1703–1706. doi: 10.3969/j.issn.1001-506X.2011.08.05 [148] 艾小凡, 罗勇江, 赵国庆. 基于张量正则分解的时频混叠信号欠定盲分离方法[J]. 航空学报, 2015, 36(10): 3393–3400. doi: 10.7527/S1000-6893.2014.0319AI Xiaofan, LUO Yongjiang, and ZHAO Guoqing. Canonical decomposition approach for underdetermined blind separation of non-disjoint sources[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3393–3400. doi: 10.7527/S1000-6893.2014.0319 [149] 葛素楠, 韩敏. 基于四阶累积张量方法的欠定盲源信号分离[J]. 电子学报, 2014, 42(5): 992–997. doi: 10.3969/j.issn.0372-2112.2014.05.025GE Su’nan and HAN Min. Fourth-order cumulant of tensor decomposition method for blind identification of underdetermined separation[J]. Acta Electronica Sinica, 2014, 42(5): 992–997. doi: 10.3969/j.issn.0372-2112.2014.05.025 [150] 李欣, 王春阳, 付孝龙, 等. 极化通道扩展和盲源分离联合抗移频干扰技术[J]. 北京航空航天大学学报, 2017, 43(4): 731–737. doi: 10.13700/j.bh.1001-5965.2016.0250LI Xin, WANG Chunyang, FU Xiaolong, et al. Shift-frequency jamming suppression technique based on polarized channel expanding and blind source separation union[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 731–737. doi: 10.13700/j.bh.1001-5965.2016.0250 [151] 李嘉辛, 王宏, 江朝抒, 等. 基于神经网络的主瓣干扰抑制技术[J]. 中国电子科学研究院学报, 2019, 14(10): 1077–1082. doi: 10.3969/j.issn.1673-5692.2019.10.014LI Jiaxin, WANG Hong, JIANG Chaoshu, et al. A neural network beamformer for main-lobe interference suppression[J]. Journal of CAEIT, 2019, 14(10): 1077–1082. doi: 10.3969/j.issn.1673-5692.2019.10.014 [152] ZHANG Yu, JIU Bo, WANG Penghui, et al. An end-to-end anti-jamming target detection method based on CNN[J]. IEEE Sensors Journal, 2021, 21(19): 21817–21828. doi: 10.1109/JSEN.2021.3103042 [153] HILL P C J and TRUFFERT V. Statistical processing techniques for detecting DRFM repeat-jam radar signals[C]. IEE Colloquium on Signal Processing Techniques for Electronic Warfare, London, UK, 1992: 1–6. [154] GRECO M, GINI F, and FARINA A. Radar detection and classification of jamming signals belonging to a cone class[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 1984–1993. doi: 10.1109/tsp.2007.909326 [155] LI Shengyuan, ZHANG Linrang, LIU Nan, et al. Adaptive detection with conic rejection to suppress deceptive jamming for frequency diverse MIMO radar[J]. Digital Signal Processing, 2017, 69: 32–40. doi: 10.1016/j.dsp.2017.06.008 [156] 赵珊珊, 张林让, 周宇, 等. 利用空间散射特性差异进行有源假目标鉴别[J]. 西安电子科技大学学报:自然科学版, 2015, 42(2): 20–27. doi: 10.3969/j.issn.1001-2400.2015.02.004ZHAO Shanshan, ZHANG Linrang, ZHOU Yu, et al. Active false-target discrimination method based on the difference in spatial scattering characteristic[J]. Journal of Xidian University, 2015, 42(2): 20–27. doi: 10.3969/j.issn.1001-2400.2015.02.004 [157] ZHAO Shanshan, ZHANG Linrang, ZHOU Yu, et al. Discrimination of active false targets in multistatic radar using spatial scattering properties[J]. IET Radar, Sonar & Navigation, 2016, 10(5): 817–826. doi: 10.1049/iet-rsn.2014.0147 [158] ZHAO Shanshan, LIU Nan, ZHANG Linrang, et al. Discrimination of deception targets in multistatic radar based on clustering analysis[J]. IEEE Sensors Journal, 2016, 16(8): 2500–2508. doi: 10.1109/jsen.2016.2516000 [159] LI Qiang, ZHANG Linrang, ZHOU Yu, et al. Hermitian distance-based method to discriminate physical targets and active false targets in a distributed multiple-radar architecture[J]. IEEE Sensors Journal, 2019, 19(22): 10432–10442. doi: 10.1109/JSEN.2019.2926414 [160] 赵艳丽, 王雪松, 王国玉, 等. 多假目标欺骗干扰下组网雷达跟踪技术[J]. 电子学报, 2007, 35(3): 454–458. doi: 10.3321/j.issn:0372-2112.2007.03.014ZHAO Yanli, WANG Xuesong, WANG Guoyu, et al. Tracking technique for radar network in the presence of multi-range-false-target deception jamming[J]. Acta Electronica Sinica, 2007, 35(3): 454–458. doi: 10.3321/j.issn:0372-2112.2007.03.014 [161] HUANG Datong, CUI Guolong, YU Xianxiang, et al. Joint range-velocity deception jamming suppression for SIMO radar[J]. IET Radar, Sonar & Navigation, 2019, 13(1): 113–122. doi: 10.1049/iet-rsn.2018.5158 [162] 黄大通. 分布式多站雷达抗欺骗干扰技术研究[D]. [硕士论文], 电子科技大学, 2019.HUANG Datong. Research on confronting deception jamming techniques in distributed multi-static radars[D]. [Master dissertation], University of Electronic Science and Technology of China, 2019. [163] 李永祯, 王雪松, 王涛, 等. 有源诱饵的极化鉴别研究[J]. 国防科技大学学报, 2004, 26(3): 83–88. doi: 10.3969/j.issn.1001-2486.2004.03.018LI Yongzhen, WANG Xuesong, WANG Tao, et al. Polarization discrimination algorithm of active decoy and radar target[J]. Journal of National University of Defense Technology, 2004, 26(3): 83–88. doi: 10.3969/j.issn.1001-2486.2004.03.018 [164] 李永祯, 王雪松, 肖顺平, 等. 基于IPPV的真假目标极化鉴别算法[J]. 现代雷达, 2004, 26(9): 38–42. doi: 10.3969/j.issn.1004-7859.2004.09.011LI Yongzhen, WANG Xuesong, XIAO Shunping, et al. A new polarization discrimination algorithm for active decoy and radar target based on IPPV[J]. Modern Radar, 2004, 26(9): 38–42. doi: 10.3969/j.issn.1004-7859.2004.09.011 [165] 李永祯, 王雪松, 肖顺平, 等. 有源假目标的高分辨极化鉴别研究[J]. 兵工学报, 2005, 26(6): 754–760. doi: 10.3321/j.issn:1000-1093.2005.06.009LI Yongzhen, WANG Xuesong, XIAO Shunping, et al. Research on high-resolution polarization discrimination algorithm of active decoy and radar target[J]. Acta Armamentarii, 2005, 26(6): 754–760. doi: 10.3321/j.issn:1000-1093.2005.06.009 [166] 王涛. 弹道中段目标极化域特征提取与识别[D]. [博士论文], 国防科技大学, 2006.WANG Tao. Feature extraction and recognition of targets in ballistic midcourse in polarization-domain[D]. [Ph. D. dissertation], National University of Defense Technology, 2006. [167] 吴盛源, 张小宽, 林存坤, 等. 双接收站的有源诱饵极化鉴别[J]. 空军工程大学学报:自然科学版, 2016, 17(3): 73–77. doi: 10.3969/j.issn.1009-3516.2016.03.014WU Shengyuan, ZHANG Xiaokuan, LIN Cunkun, et al. A discrimination method of active decoy polarization based on two receiving stations[J]. Journal of Air Force Engineering University:Natural Science Edition, 2016, 17(3): 73–77. doi: 10.3969/j.issn.1009-3516.2016.03.014 [168] 常宇亮, 李永祯, 戴幻尧, 等. 全极化复杂调制假目标的鉴别方法[J]. 电波科学学报, 2010, 25(4): 651–657. doi: 10.13443/j.cjors.2010.04.015CHANG Yuliang, LI Yongzhen, DAI Huanyao, et al. Distinguish method of polarimetric complicated modulation decoy[J]. Chinese Journal of Radio Science, 2010, 25(4): 651–657. doi: 10.13443/j.cjors.2010.04.015 [169] 李泽江. 弹道目标动态极化特性分析及鉴别方法研究[D]. [硕士论文], 国防科学技术大学, 2013.LI Zejiang. Dynamic polarization characteristic analysis and discrimination methods of ballistic targets[D]. [Master dissertation], National University of Defense Technology, 2013. [170] 赫彬, 苏洪涛. 一种多目标与多基地雷达之间的博弈策略[J]. 西安电子科技大学学报, 2021, 48(2): 125–132. doi: 10.19665/j.issn1001-2400.2021.02.016HE Bin and SU Hongtao. Study of game strategy between multiple targets and multistatics radars[J]. Journal of Xidian University, 2021, 48(2): 125–132. doi: 10.19665/j.issn1001-2400.2021.02.016 [171] SONG Xiufeng, WILLETT P, ZHOU Shengli, et al. The MIMO radar and jammer games[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 687–699. doi: 10.1109/TSP.2011.2169251 [172] PIEZZO M, AUBRY A, BUZZI S, et al. Non-cooperative code design in radar networks: A game-theoretic approach[J]. EURASIP Journal on Advances in Signal Processing, 2013, 2013(1): 63. doi: 10.1186/1687-6180-2013-63 [173] JIANG Xiaofeng, ZHOU Feng, CHEN Shuangwu, et al. Jamming resilient tracking using POMDP-based detection of hidden targets[J]. IEEE Transactions on Information Forensics and Security, 2021, 16: 983–998. doi: 10.1109/TIFS.2020.3027145 [174] 陶庭宝, 张弓, 张劲东. 有源压制干扰下的相控阵雷达多目标跟踪时间资源优化配置算法[J]. 数据采集与处理, 2020, 35(5): 978–990. doi: 10.16337/j.1004-9037.2020.05.018TAO Tingbao, ZHANG Gong, and ZHANG Jindong. Optimal algorithm of time resource allocation for multiple target tracking of phased array radar under active oppressive jamming[J]. Journal of Data Acquisition and Processing, 2020, 35(5): 978–990. doi: 10.16337/j.1004-9037.2020.05.018 [175] DELIGIANNIS A, ROSSETTI G, PANOUI A, et al. Power allocation game between a radar network and multiple jammers[C]. 2016 IEEE Radar Conference, Philadelphia, USA, 2016: 1–5. [176] DELIGIANNIS A, LAMBOTHARAN S, and CHAMBERS J A. Game theoretic analysis for MIMO radars with multiple targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(6): 2760–2774. doi: 10.1109/TAES.2016.150699 [177] LI Kang, JIU Bo, WANG Penghui, et al. Radar active antagonism through deep reinforcement learning: A Way to address the challenge of mainlobe jamming[J]. Signal Processing, 2021, 186: 108130. doi: 10.1016/j.sigpro.2021.108130 [178] LI Kang, JIU Bo, PU Wenqiang, et al. Neural fictitious self-play for radar anti-jamming dynamic game with imperfect information[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022. [179] SHI Chenguang, QIU Wei, WANG Fei, et al. Power control scheme for spectral coexisting multistatic radar and massive MIMO communication systems under uncertainties: A robust Stackelberg game model[J]. Digital Signal Processing, 2019, 94: 146–155. doi: 10.1016/j.dsp.2019.05.007 [180] KHAN Z, LEHTOMÄKI J J, AGUILAR-GONZALEZ R, et al. Database-assisted distributed and cloud-based access methods for unlicensed and radar bands[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(3): 404–419. doi: 10.1109/TCCN.2017.2733533 [181] 聂红霞. 雷达抗干扰效能评估方法探讨[J]. 舰船电子工程, 2013, 33(4): 75–77. doi: 10.3969/j.issn.1627-9730.2013.04.025NIE Hongxia. Evaluation method of radar anti-jamming effect[J]. Ship Electronic Engineering, 2013, 33(4): 75–77. doi: 10.3969/j.issn.1627-9730.2013.04.025 [182] 周万幸. 雷达抗干扰效能评估模型与指标体系研究[J]. 现代雷达, 2013, 35(11): 1–5. doi: 10.16592/j.cnki.1004-7859.2013.11.019ZHOU Wanxing. A study on model and index system of radar anti-jamming effectiveness[J]. Modern Radar, 2013, 35(11): 1–5. doi: 10.16592/j.cnki.1004-7859.2013.11.019 [183] 陈文东, 汤斌. 复杂电磁环境下雷达抗干扰性能评估方法[J]. 雷达科学与技术, 2017, 15(1): 73–80. doi: 10.3969/j.issn.1672-2337.2017.01.013CHEN Wendong and TANG Bin. A radar ECCM performance evaluation method in complex electromagnetic environment[J]. Radar Science and Technology, 2017, 15(1): 73–80. doi: 10.3969/j.issn.1672-2337.2017.01.013 [184] 崔啸, 孟祥东, 叶玲平, 等. 基于数字化样机的机载雷达模型仿真与作战效能评估[J]. 现代雷达, 2021, 43(5): 32–37. doi: 10.16592/j.cnki.1004-7859.2021.05.005CUI Xiao, MENG Xiangdong, YE Lingping, et al. Model simulation and operational effectiveness evaluation for airborne radar system based on digital prototype[J]. Modern Radar, 2021, 43(5): 32–37. doi: 10.16592/j.cnki.1004-7859.2021.05.005 [185] 孟晋丽, 傅有光, 陈翼, 等. 雷达抗干扰效能指标体系与评估方法[J]. 现代雷达, 2014, 36(11): 80–84. doi: 10.16592/j.cnki.1004-7859.2014.11.019MENG Jinli, FU Youguang, CHEN Yi, et al. Index system and evaluation of radar anti-jamming effectiveness[J]. Modern Radar, 2014, 36(11): 80–84. doi: 10.16592/j.cnki.1004-7859.2014.11.019 [186] 何小锋. 雷达综合抗干扰效能评估方法指标研究[J]. 雷达与对抗, 2020, 40(3): 11–15. doi: 10.19341/j.cnki.issn.1009-0401.2020.03.003HE Xiaofeng. Research on evaluation methods of radar anti-jamming efficiency[J]. Radar &ECM, 2020, 40(3): 11–15. doi: 10.19341/j.cnki.issn.1009-0401.2020.03.003 [187] 段蕾, 诸四海. 面向全过程的机载预警雷达效能评估技术研究[J]. 中国电子科学研究院学报, 2019, 14(7): 756–762. doi: 10.3969/j.issn.1673-5692.2019.07.016DUAN Lei and ZHU Sihai. Research on whole-process oriented effectiveness evaluation of AEW radar[J]. Journal of CAEIT, 2019, 14(7): 756–762. doi: 10.3969/j.issn.1673-5692.2019.07.016 [188] 张宏斌, 杨杰, 郭宇峰. 直升机多机协同探测效能评估指标体系构建[J]. 直升机技术, 2020(3): 19–21.ZHANG Hongbin, YANG Jie, and GUO Yufeng. Establishing for efficiency evaluation index system of helicopters coordination detection[J]. Helicopter Technique, 2020(3): 19–21. [189] 朱兴乐. 雷达组网系统效能评估指标体系设计[J]. 舰船电子对抗, 2019, 42(5): 48–51, 91. doi: 10.16426/j.cnki.jcdzdk.2019.05.012ZHU Xingle. Design of efficiency evaluation index system of radar networking system[J]. Shipboard Electronic Countermeasure, 2019, 42(5): 48–51, 91. doi: 10.16426/j.cnki.jcdzdk.2019.05.012 [190] 肖振民, 代培龙, 沈伟, 等. 基于AHP的分布式雷达抗干扰效能评估方法[J]. 现代雷达, 2017, 39(1): 77–83. doi: 10.16592/j.cnki.1004-7859.2017.01.018XIAO Zhenmin, DAI Peilong, SHEN Wei, et al. Method of anti-jamming effectiveness evaluation for distributed radar based on AHP[J]. Modern Radar, 2017, 39(1): 77–83. doi: 10.16592/j.cnki.1004-7859.2017.01.018 [191] 郭万海, 邵晓方, 滕俊. 基于层次熵分析法的舰载雷达抗干扰效能评估[J]. 舰船电子工程, 2014, 34(8): 59–62. doi: 10.3969/j.issn1672-9730.2014.08.017GUO Wanhai, SHAO Xiaofang, and TENG Jun. Efficiency evaluation of shipboard radar ECCM based on AHP and entropy technology[J]. Ship Electronic Engineering, 2014, 34(8): 59–62. doi: 10.3969/j.issn1672-9730.2014.08.017 [192] 宋宝军, 张秦, 姜军. 基于Vague集模糊值线性序法的雷达抗干扰效能评估[J]. 火力与指挥控制, 2016, 41(2): 124–127. doi: 10.3969/j.issn.1002-0640.2016.02.031SONG Baojun, ZHANG Qin, and JIANG Jun. Anti-jamming effectiveness evaluation technology research of radar based on Vague sets and fuzzy liner ranking[J]. Fire Control &Command Control, 2016, 41(2): 124–127. doi: 10.3969/j.issn.1002-0640.2016.02.031 [193] 孟宪猛, 蔡翠翠, 张东. 基于多层次模糊算法的雷达抗干扰性能分析[J]. 舰船电子工程, 2017, 37(4): 59–62. doi: 10.3969/j.issn.1672-9730.2017.04.016MENG Xianmeng, CAI Cuicui, and ZHANG Dong. Radar anti-jamming performance analysis based on multi-level fuzzy algorithm[J]. Ship Electronic Engineering, 2017, 37(4): 59–62. doi: 10.3969/j.issn.1672-9730.2017.04.016 [194] 徐沙, 张洁. 一种基于层次分析法的雷达抗干扰效能评估方法[J]. 航天电子对抗, 2016, 32(3): 13–15. doi: 10.3969/j.issn.1673-2421.2016.03.004XU Sha and ZHANG Jie. An evaluation method of radar anti-jamming efficiency based on analytical hierarchy process[J]. Aerospace Electronic Warfare, 2016, 32(3): 13–15. doi: 10.3969/j.issn.1673-2421.2016.03.004 [195] 薛军帅, 张迪, 黄勇, 等. 一种基于AHP-可拓云的雷达系统效能评估方法[J]. 兵工自动化, 2022, 41(4): 81–86, 92. doi: 10.7690/bgzdh.2022.04.017XUE Junshuai, ZHANG Di, HUANG Yong, et al. A radar system effectiveness evaluation method based on AHP-extension cloud[J]. Ordnance Industry Automation, 2022, 41(4): 81–86, 92. doi: 10.7690/bgzdh.2022.04.017 [196] 袁超鹏, 李江. 基于支持向量机的雷达网抗干扰效能评估[J]. 电子科技, 2014, 27(9): 101–103. doi: 10.16180/j.cnki.issn1007-7820.2014.09.005YUAN Chaopeng and LI Jiang. Evaluation of radar net anti-jamming capacity based on SVM[J]. Electronic Science and Technology, 2014, 27(9): 101–103. doi: 10.16180/j.cnki.issn1007-7820.2014.09.005 [197] 徐斐, 谢洲烨, 沈伟, 等. 基于神经网络的分布式雷达抗干扰效能评估方法[J]. 现代雷达, 2015, 37(7): 4–7, 11. doi: 10.16592/j.cnki.1004-7859.2015.07.002XU Fei, XIE Zhouye, SHEN Wei, et al. A method of anti-jamming effectiveness evaluation for distributed radar based on neural network[J]. Modern Radar, 2015, 37(7): 4–7, 11. doi: 10.16592/j.cnki.1004-7859.2015.07.002 [198] 姬正一, 陈阳, 沈培志, 等. 决策树集成方法在反舰导弹效能评估中的应用[J]. 现代防御技术, 2021, 49(4): 15–23, 34. doi: 10.3969/j.issn.1009-086x.2021.04.003JI Zhengyi, CHEN Yang, SHEN Peizhi, et al. Decision tree integration method application in effectiveness evaluation of anti-ship missile weapon system[J]. Modern Defence Technology, 2021, 49(4): 15–23, 34. doi: 10.3969/j.issn.1009-086x.2021.04.003 [199] 周立锋. 基于主成分分析的测量雷达效能评估方法[J]. 现代雷达, 2019, 41(2): 7–9, 25. doi: 10.16592/j.cnki.1004-7859.2019.02.002ZHOU Lifeng. Method of measurement radar effectiveness based on principal components analysis[J]. Modern Radar, 2019, 41(2): 7–9, 25. doi: 10.16592/j.cnki.1004-7859.2019.02.002 [200] 余显祥, 路晴辉, 杨婧, 等. 短基线收发分置频域协同波形设计方法[J]. 雷达学报, 2022, 11(2): 227–239. doi: 10.12000/JR22014YU Xianxiang, LU Qinghui, YANG Jing, et al. Frequency domain cooperative waveform design method for short baseline transceiver[J]. Journal of Radars, 2022, 11(2): 227–239. doi: 10.12000/JR22014 期刊类型引用(29)
1. 张锐,龚汉钦,宋瑞源,李亚东,卢智,张东恒,胡洋,陈彦. 基于4D成像雷达的隔墙人体姿态重建与行为识别研究. 雷达学报(中英文). 2025(01): 44-61 .  百度学术
百度学术2. 陈彦,张锐,李亚东,宋瑞源,耿瑞旭,龚汉钦,汪斌全,张东恒,胡洋. 基于无线信号的人体姿态估计综述. 雷达学报(中英文). 2025(01): 229-247 .  百度学术
百度学术3. 吴振华,崔金鑫,曹宜策,张强,张磊,杨利霞. 零记忆增量学习的复合有源干扰识别. 电子与信息学报. 2025(01): 188-200 .  百度学术
百度学术4. 李亚南,韩壮志,王凯,刘得军. 基于半实物仿真的雷达抗干扰性能测试实验研究. 实验技术与管理. 2025(02): 104-110 .  百度学术
百度学术5. 张永鹏. 制导雷达智能处理技术现状和发展趋势. 电子技术应用. 2025(03): 25-31 .  百度学术
百度学术6. 江达伟,董阳阳,张立东,路宵,董春曦. 基于深度学习的空中目标威胁评估技术研究. 系统仿真学报. 2025(03): 791-802 .  百度学术
百度学术7. 兰岚,张翔,许京伟,廖桂生. 阵列雷达时空多维域编码抗主瓣转发式欺骗干扰方法. 雷达学报(中英文). 2025(02): 439-455 .  百度学术
百度学术8. 刘蕾,吕永乐. 基于模糊云模型的雷达抗干扰智能化水平评估方法研究. 计算机测量与控制. 2025(04): 313-321 .  百度学术
百度学术9. 郭新宝,郭胜龙,刘世阳,戴扶摇. 典型环境极化对抗有源干扰技术研究. 战术导弹技术. 2025(02): 139-146 .  百度学术
百度学术10. 贾金伟,高敏,韩壮志,刘利民,尹园威. 无线电近炸引信抗信息型干扰技术研究综述. 系统工程与电子技术. 2025(04): 1074-1107 .  百度学术
百度学术11. 张嘉翔,张凯翔,梁振楠,陈新亮,刘泉华. 一种基于深度强化学习的频率捷变雷达智能频点决策方法. 雷达学报. 2024(01): 227-239 .  本站查看
本站查看12. 朱梦韬,张露瑶,李瑞,杨静. 基于HMM的逆雷达辐射源状态识别推理方法. 北京理工大学学报. 2024(02): 200-209 .  百度学术
百度学术13. 陈圣贤,胡明,李永龙,袁雪林. 超宽带脉冲作用下抗干扰器件的特性分析. 强激光与粒子束. 2024(01): 66-73 .  百度学术
百度学术14. 王沙飞,朱梦韬,李云杰,杨健,李岩. 对先进多功能雷达系统行为的识别、推理与预测:综述与展望. 信号处理. 2024(01): 17-55 .  百度学术
百度学术15. 方愚渊,魏嵩,何超,孙一心,张磊,王明宇. 雷达对抗技术研究综述与智能反干扰展望. 信息对抗技术. 2024(02): 5-26 .  百度学术
百度学术16. 贲德. 机载有源相控阵火控雷达技术发展. 现代雷达. 2024(02): 1-15 .  百度学术
百度学术17. 刘尚富,李炜杰. EA-18G作战能力及雷达对抗策略分析. 雷达与对抗. 2024(02): 7-10+24 .  百度学术
百度学术18. 周长霖,王春阳,陈赓,刘明杰. 雷达主瓣反干扰研究进展及展望. 信息对抗技术. 2024(04): 1-16 .  百度学术
百度学术19. 江凯. 空天基合成孔径雷达多域抗干扰技术综述. 雷达科学与技术. 2024(04): 355-368 .  百度学术
百度学术20. 郭文杰,吴振华,曹宜策,张强,张磊,杨利霞. 多域浅层特征引导下雷达有源干扰多模态对比识别方法. 雷达学报. 2024(05): 1004-1018 .  本站查看
本站查看21. 齐铖,谢军伟,张浩为,王瑞君,黄洁瑜. 基于防空目标探测与跟踪的雷达资源管理技术研究综述. 信号处理. 2024(11): 1972-1989 .  百度学术
百度学术22. 戴少怀,许天放,殷佳伟,余科,沈涛. 大模型驱动的干扰对抗典型应用和关键技术分析. 航天电子对抗. 2024(06): 1-5 .  百度学术
百度学术23. 吕大鑫,杨超群. 一种面向无人侦察机的通信受限干扰源跟踪方法. 无人系统技术. 2023(02): 13-21 .  百度学术
百度学术24. 李康,纠博,赵宇,刘宏伟. 雷达智能博弈抗干扰技术综述与展望. 现代雷达. 2023(05): 15-26 .  百度学术
百度学术25. 胡惠. 频率相位联合编码的低截获雷达波形优化设计方法. 电声技术. 2023(02): 65-68 .  百度学术
百度学术26. 李欣宇,罗雨,叶薇薇,许娟,董硕. 高集成雷达系统激励器的设计与分析. 数字技术与应用. 2023(08): 157-159 .  百度学术
百度学术27. 徐聪,郭子林,王学尧,骆林,王洪林,刘维建. 国外预警机发展现状及雷达关键技术研究. 空天预警研究学报. 2023(02): 79-88 .  百度学术
百度学术28. 吴呈瑜,张红斌,占敖. 低信噪比场景下全相位FFT载频估计改进算法. 无线电通信技术. 2023(06): 1073-1080 .  百度学术
百度学术29. 解烽,刘环宇,胡锡坤,钟平,李君宝. 基于复数域深度强化学习的多干扰场景雷达抗干扰方法. 雷达学报. 2023(06): 1290-1304 .  本站查看
本站查看其他类型引用(16)
-



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公


 下载:
下载:
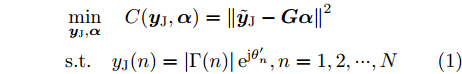
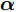
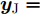

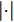

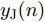
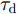
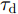
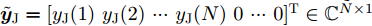
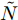
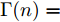
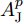
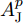
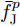
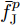
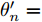
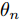
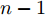
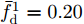
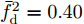
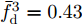
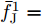
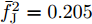
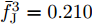
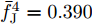
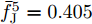
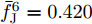
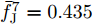
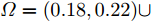
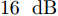

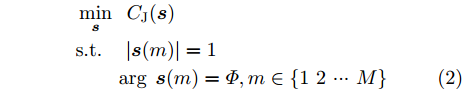
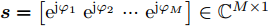
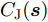
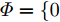
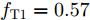
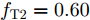
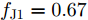
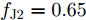
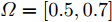
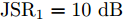
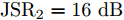

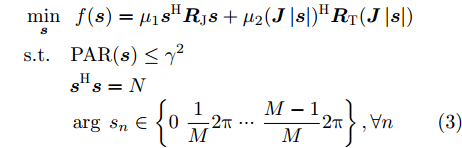
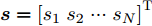
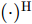
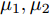
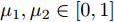
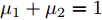
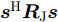
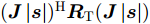
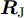
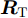
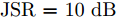
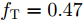
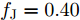
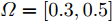
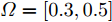
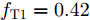
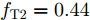
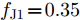
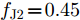
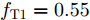
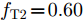
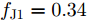
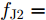
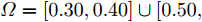

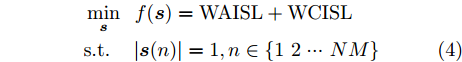
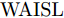
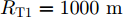
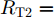
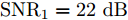
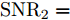
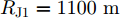
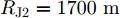
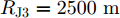
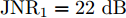
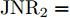
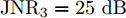
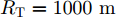



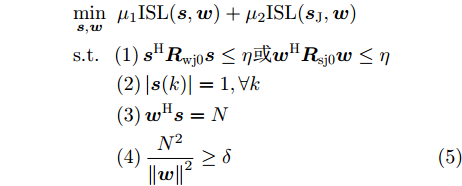
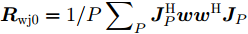
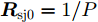
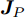
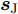
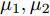
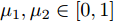
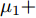
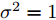



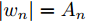
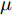
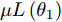
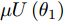
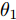
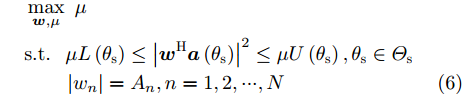
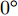
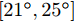
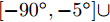
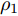
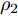
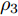


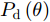
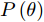
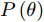
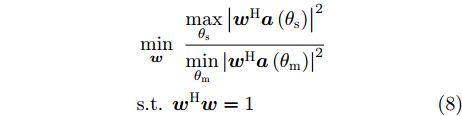
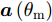
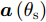
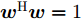
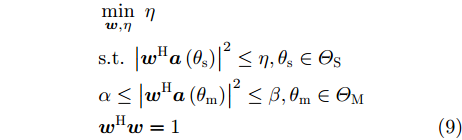
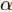
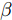
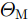
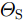
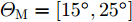
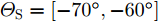
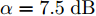
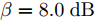
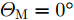
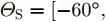
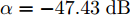
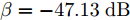

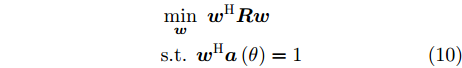
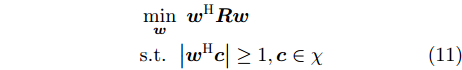
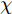
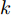
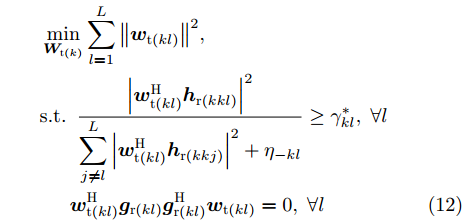
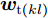
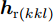
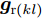
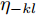
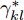
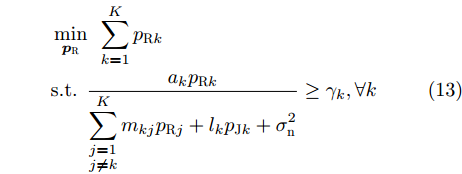
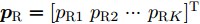
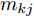
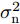
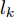
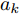
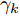
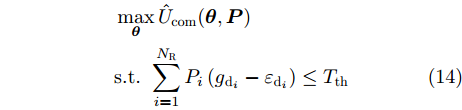
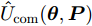
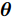
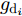
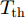
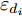
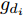
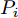
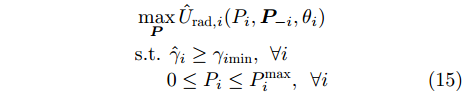
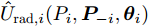
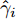

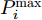
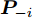

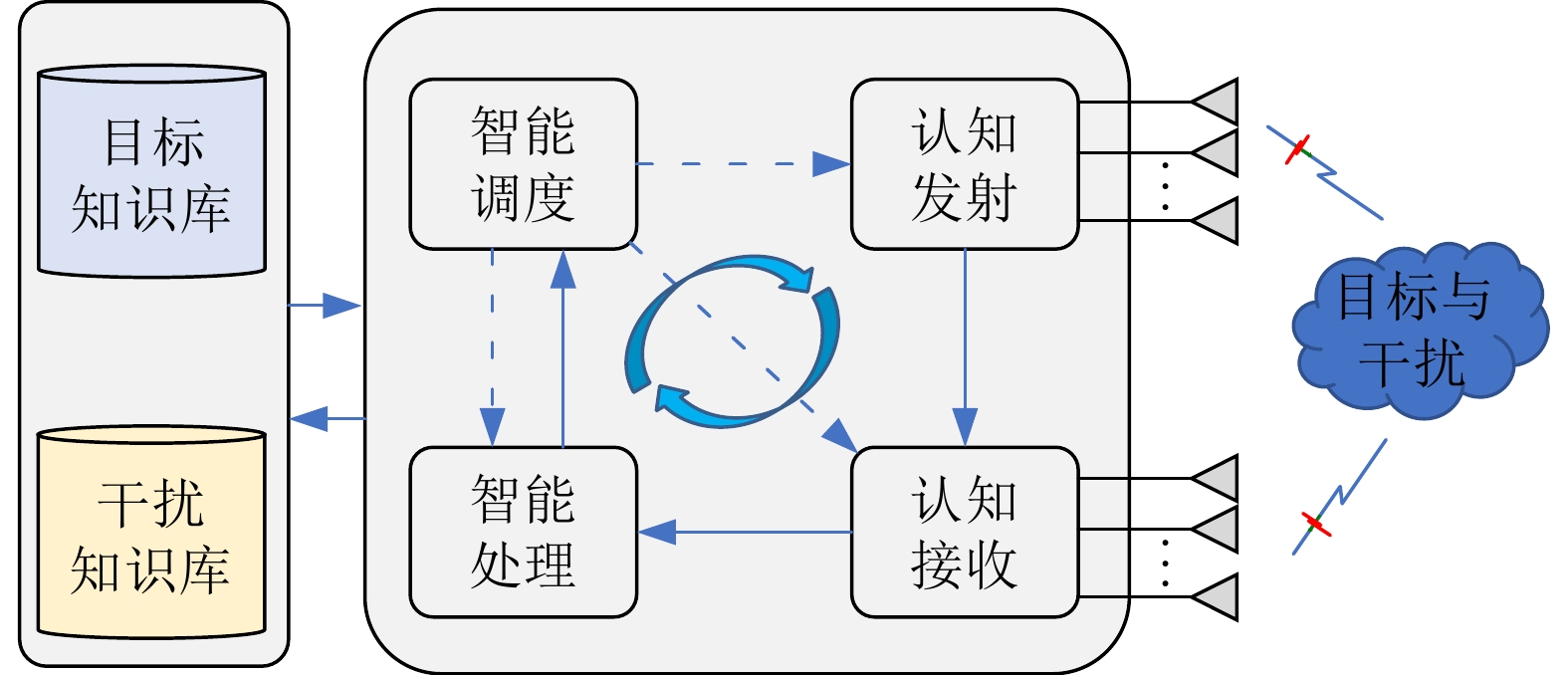
 下载:
下载:
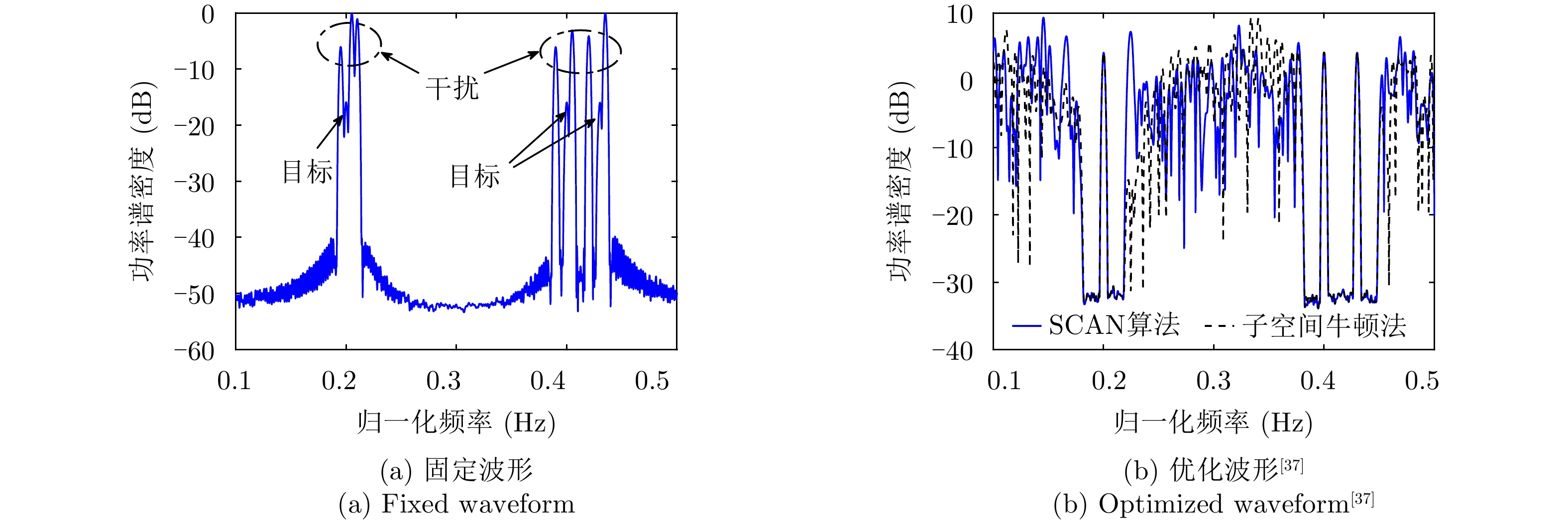
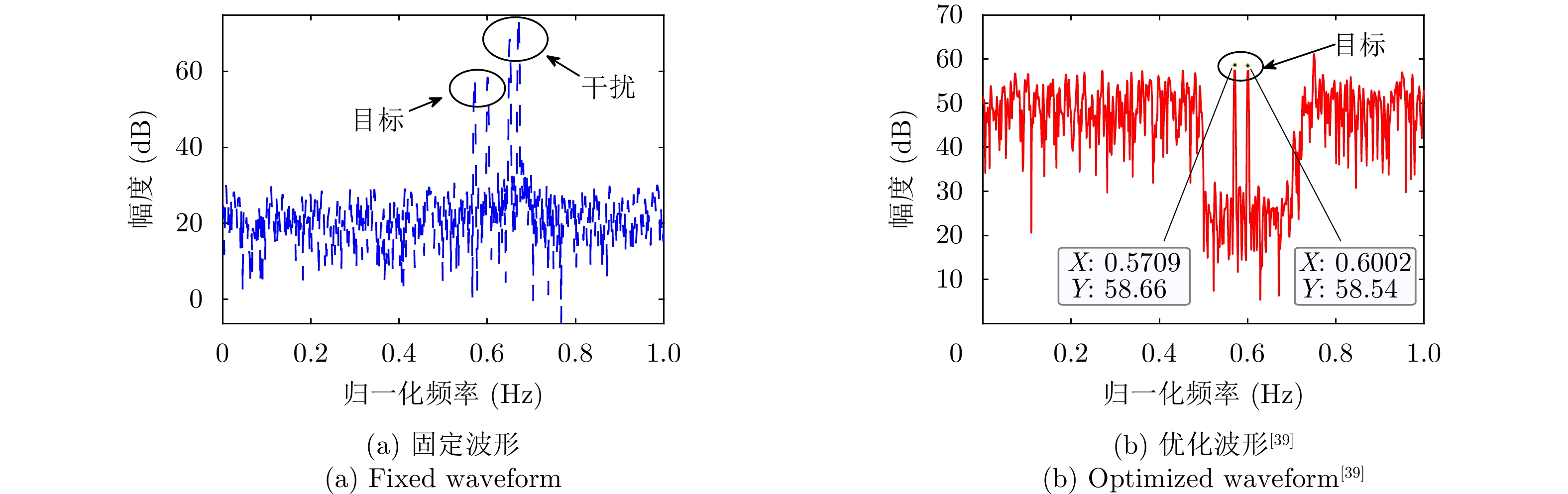

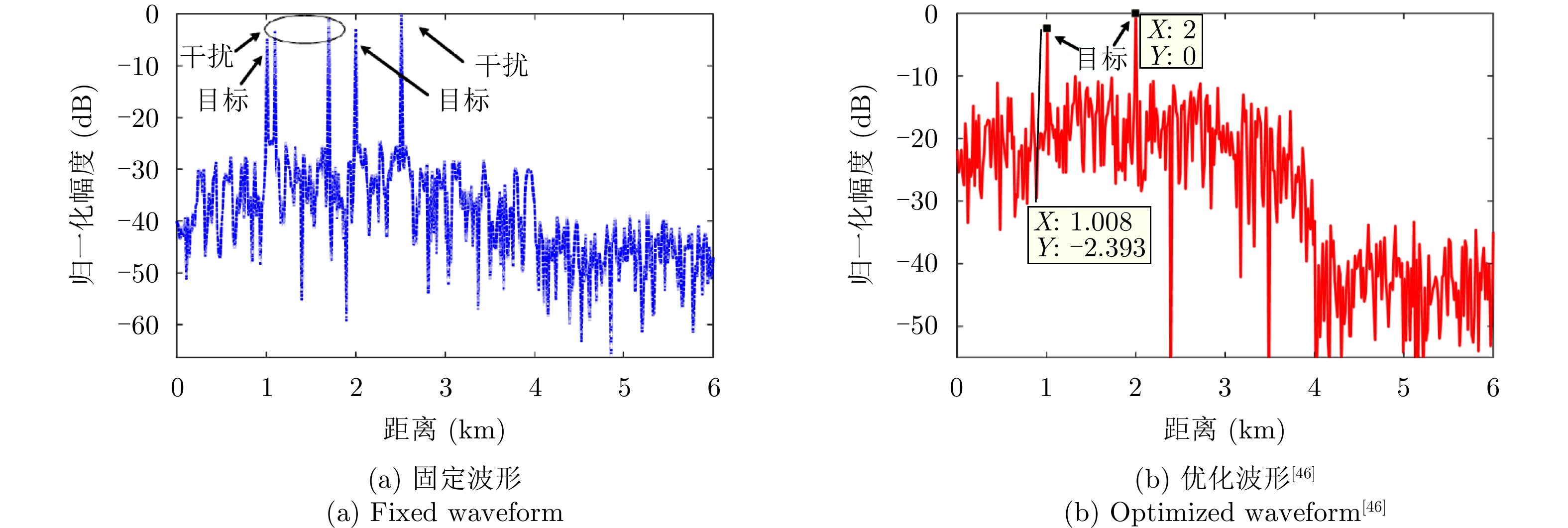
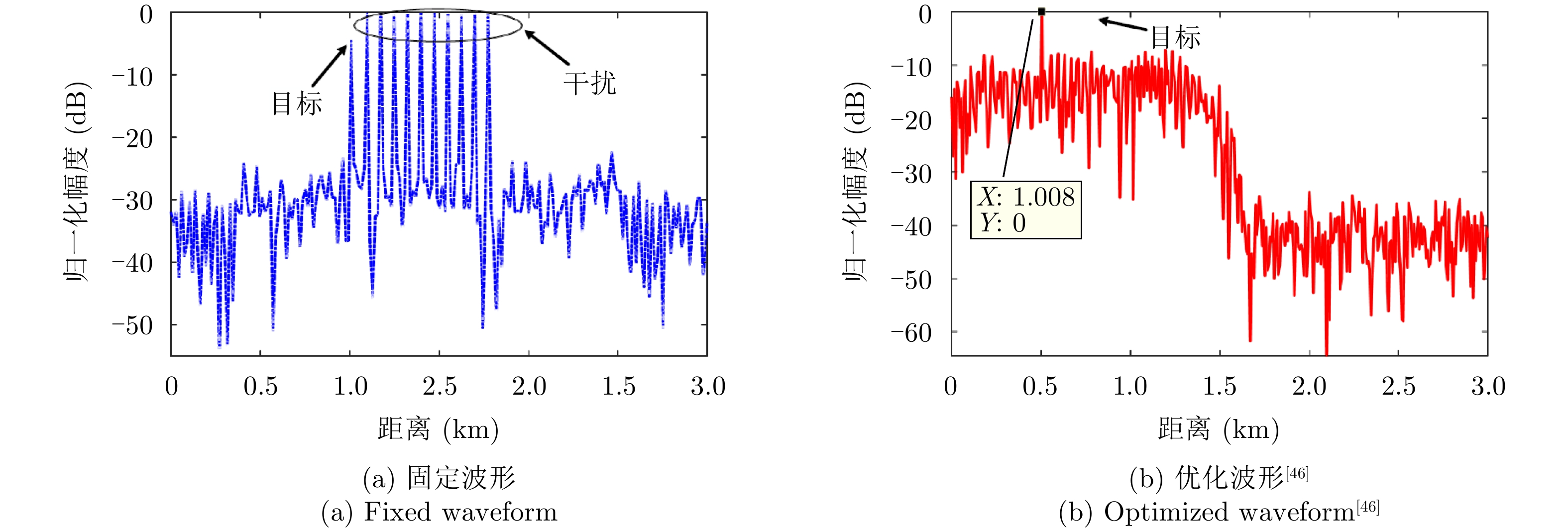
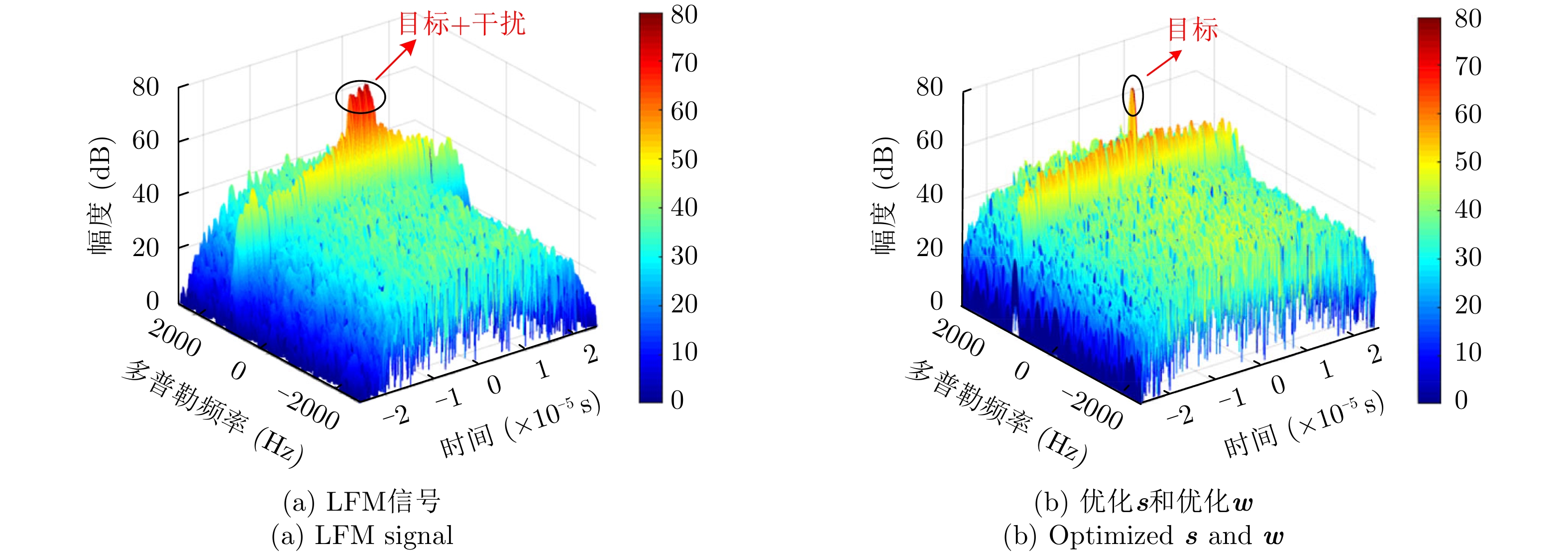
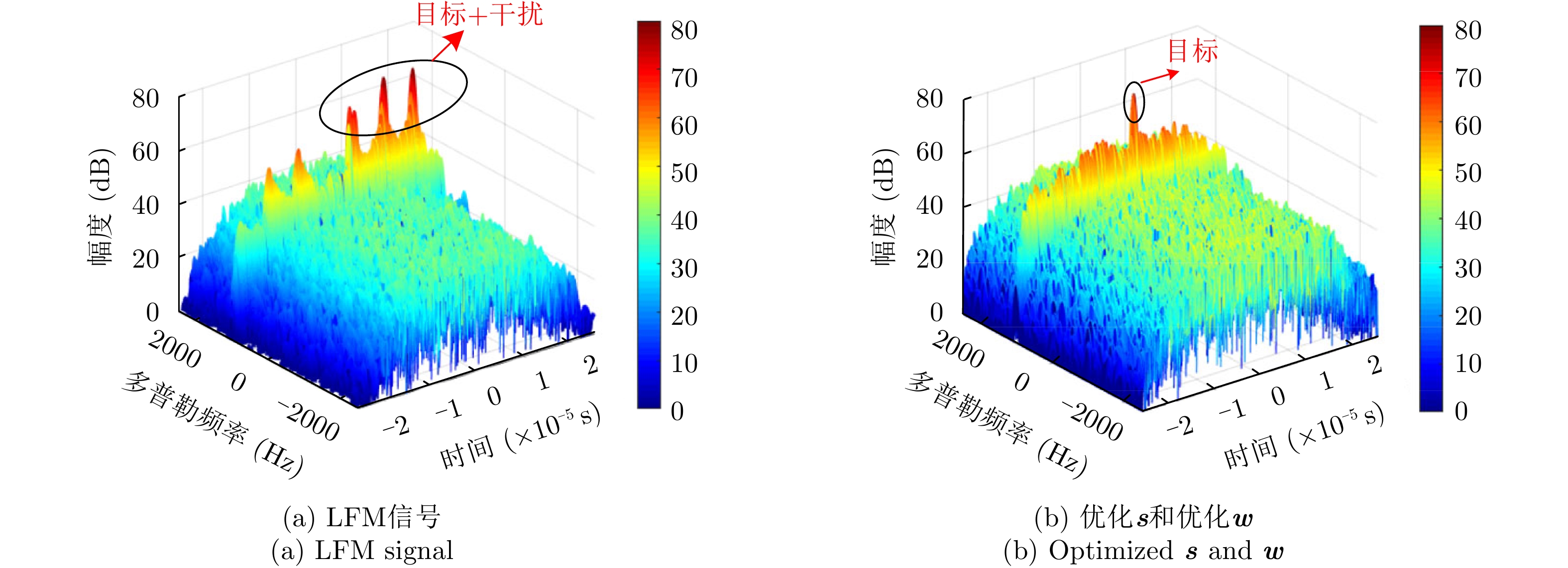

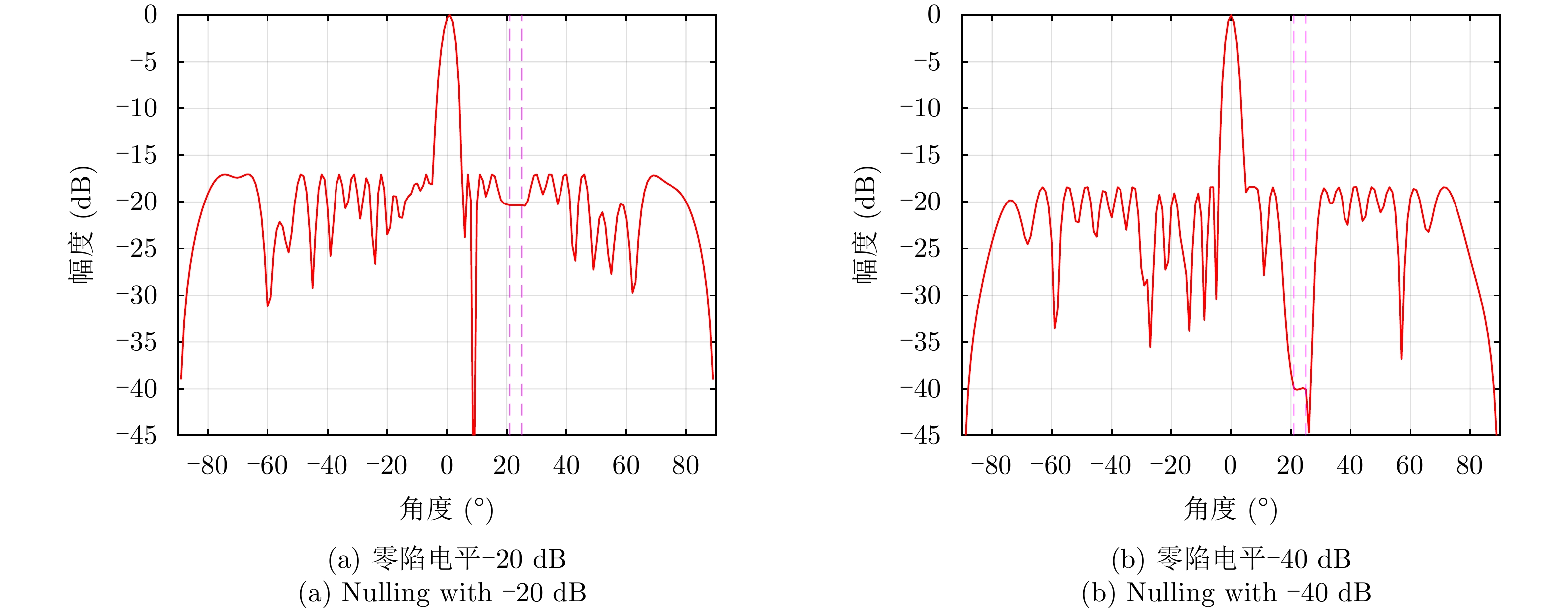
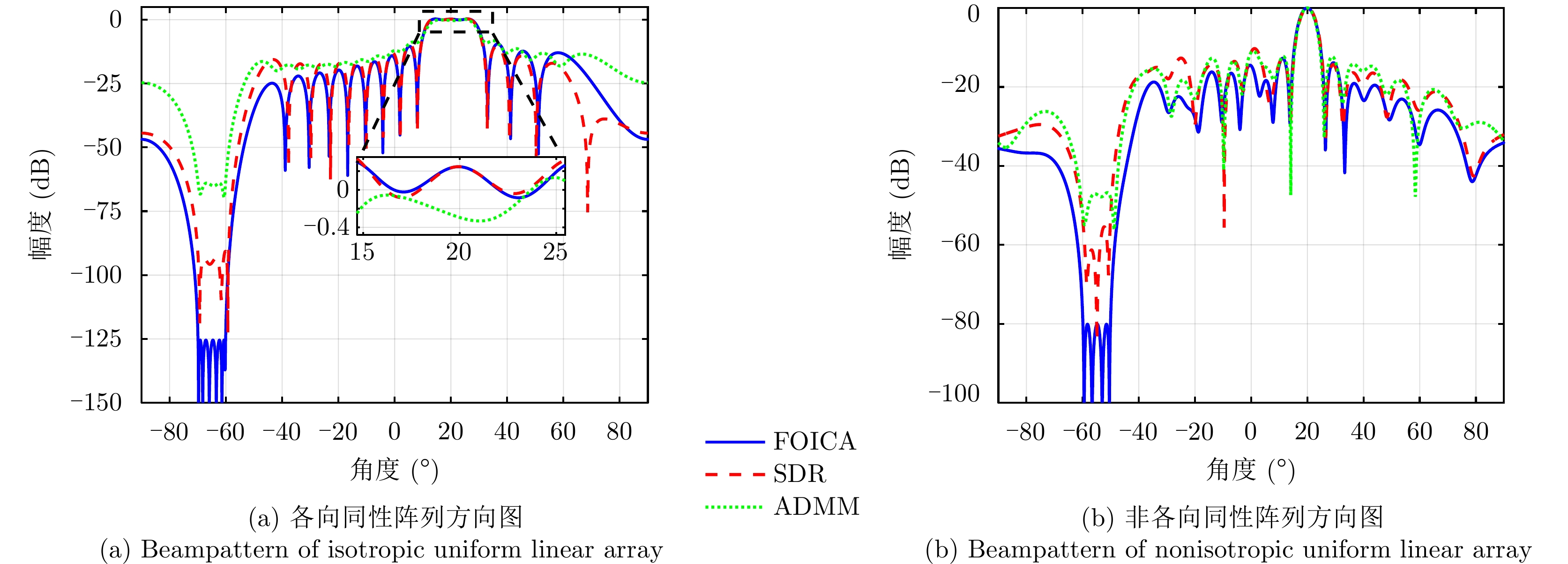
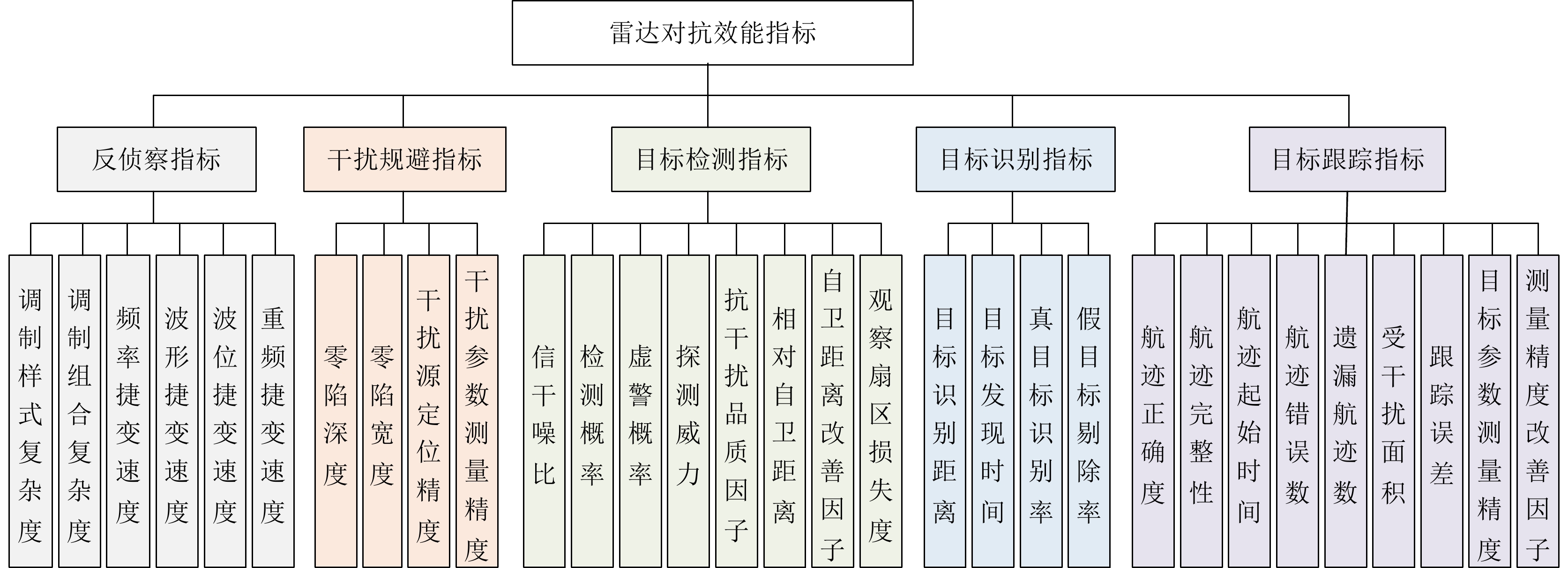
 百度学术
百度学术