Joint Waveform Optimization and Antenna Position Selection for MIMO Radar Beam Scanning
-
摘要: 为实现集中式多输入多输出(MIMO)雷达波束扫描,本文在峰值平均功率比(PAPR)、能量以及布尔(天线位置选择)约束下,基于min-max波束图匹配准则,首次提出MIMO雷达天线位置和多组探测波形(一组波形对应一个独立的波束图)的联合优方法。由于非凸PAPR约束、布尔约束以及min-max目标函数的非凸非光滑性导致了优化问题成为典型的大规模NP-难问题。为求解该NP-难优化问题,该文首先利用Lawson算法将min-max问题转化为迭代加权最小二乘(ILS)问题,然后根据上界函数最小化(MM)准则简化ILS优化问题,最后用交替方向乘子法(ADMM)求解简化后的上界优化问题。数值仿真结果检验了所提算法的有效性。
-
关键词:
- MIMO雷达发射波束图 /
- 峰值平均功率比(PAPR) /
- 稀疏阵列天线 /
- 天线选择 /
- Lawson算法 /
- 上界函数最小化(MM) /
- 交替方向乘子法(ADMM)
Abstract: In this study, under the Peak-to-Average Power Ratio (PAPR), energy, and binary (for antenna position selection) constraints, we proposed an antenna position selection and beam scanning method for colocated Multiple-Input Multiple-Output (MIMO) radar system using the min-max beampattern amplitude matching criterion. In our design, antenna positions and a set of probing waveforms were jointly determined to match a set of beampattern masks, and hence realize the beam scan. The resultant problem was large-scale, nonconvex, nonsmooth, and typical nondeterministic hard, because of the PAPR and nonconvex binary constraints, and the max and modulus operations in the objective function. To address these issues, we first transformed the min-max problem into the Iterative weighted Least Squares (ILS) problem using the Lawson algorithm, replaced the nonsmooth nonconvex objective function with the convex majorization function, and finally applied the alternating direction method of multipliers to solve the majorized ILS problem. Finally, several numerical examples were given to show the effectiveness of the proposed algorithms. -
1. 引言
集中式多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达通过不同发射天线发射不同探测波形形成特定的发射方向图,良好的发射波束图可有效降低杂波对雷达系统的干扰和提高雷达系统对波达方向不精确已知目标探测的鲁棒性[1-7]。在雷达应用中,雷达天线通常会辐射多种不同的波束图(如波束扫描)来满足不同探测任务的需求[8-13]。通常集中式MIMO雷达通过发射不同的探测波形集实现发射波束的变化,但当集中式MIMO雷达系统使用稀疏天线阵时①,传统的MIMO雷达发射波束图合成方法,如文献[1-4],因仅考虑均匀线阵(Uniform Linear Array, ULA)配置而无法满足多波束变化要求,而现有MIMO雷达稀疏天线阵设计技术因为在设计中只合成一个波束,如文献[14-16],使得其在多波束的应用场景中可能不是最佳的。本文就MIMO雷达天线位置选择的多波束扫描算法展开研究。
集中式MIMO雷达发射波束图合成的研究工作可分为两类。第1类采用两步策略,即首先优化波形协方差矩阵形成特定的发射波束图[4,11,12,17],然后根据得到的协方差矩阵设计一组雷达发射波形[18,19]。例如,文献[4]提出了一种最小旁瓣波束图设计准则优化波形协方差矩阵,然后利用循环算法优化具有理想PAPR的MIMO雷达探测波形[16,18]。文献[11]基于加权最小二乘波束图匹配准则优化具有特定发射波束图的波形协方差矩阵。其他两步设计方法详见文献[12,17,19-21]。通常这种两步策略存在很大拟合误差。第2类是直接设计波形合成预期的发射波束图以避免两步法的拟合误差问题[3,5,13,22]。例如,文献[5]提出了一种连续闭式解的方法来优化恒模探测波形。文献[22]基于最小二乘波束图匹配准则直接优化波形,并利用半定松弛(SemiDefinite Relaxation, SDR)方法求解4次优化问题,但该方法计算复杂度太高,难以满足实际应用需求。文献[3,23,24]提出了基于交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)的恒模波形设计方法。其他直接设计方法可参考文献[13,25-28]。
目前也有学者研究了集中式MIMO雷达发射波束图合成的天线位置选择方法,如文献[14,15,29],但这些研究只考虑了波形协方差矩阵的优化,没有设计波形。此外,上述研究在其设计中只考虑合成一个发射方向图,使得该方法所选天线位置对于多波束图任务可能不是最优的[30]。虽然文献[8,31,32]提出了稀疏天线阵的多波束合成技术,但这些方法只适用于相控阵,因为集中式MIMO雷达波束图与其每个发射天线所发射的波形密切相关,通常要考虑如恒模、峰值均公比(Peak-to-Average Power Ratio, PAPR)等波形约束[33-38],使得此类技术不能直接用于集中式MIMO雷达。基于此,本文提出MIMO雷达的多组探测波形和天线位置联合优化技术,满足现实中雷达波束扫描任务和天线位置优化。本文贡献总结如下:
(1) 提出多组探测波形和天线位置联合优化的波束图匹配设计方法,以实现MIMO雷达波束扫描任务。本文设计准则可以实现具有等纹波特性的发射波束图,即保证得到的波束图的旁瓣处于同一电平,主瓣电平波纹相同。文献[13,39-41]指出,波束图的这种等纹波特性可提高雷达系统对方向不精确已知目标探测的鲁棒性,还可降低雷达杂波对雷达系统的影响;与文献[8,14,15,31,32]不同,本文直接设计多组探测波形,在合成多波束的同时优化集中式MIMO雷达的天线位置。
(2) 由于天线位置参数以指数形式存在于阵列导向矢量中,直接优化天线位置参数十分困难。为有效克服这一难题,本文假设一定数量的天线位置可用于天线放置,然后引入布尔类型选择向量,将天线位置优化问题转化为天线位置选择问题,有效降低了问题建模的复杂度。
(3) 基于本文的设计准则所形成的优化问题是非凸、非光滑、大规模的NP-难问题。为有效求解此问题,首先,本文采用Lawson算法[42-44]将min-max问题转化为迭代加权最小二乘(Iterative weighted Least Squares, ILS)问题;然后,本文结合ADMM[45-47]和MM (Majorization-Minimization)[48-51]提出了一种组合优化技术,即Majorization-ADMM (M-ADMM)来简化和求解转化后的约束ILS优化问题。
符号定义:
$ {( \cdot )^ * } $ ,$ {( \cdot )^{\text{T}}} $ 以及$ {( \cdot )^{\text{H}}} $ 分别表示复共轭、转置和共轭转置。$ {{\boldsymbol{I}}_N} $ 表示维度为$ N \times N $ 的单位矩阵。$ {X_{n,l}},{{\boldsymbol{X}}_{n,:}},{{\boldsymbol{X}}_{:,l}} $ 分别表示矩阵X对应的第$ (n,l) $ 个元素、第n行以及第l列。$ {\text{diag}}({\boldsymbol{a}}) $ 表示由向量${\boldsymbol{a}} = {[{a_1},{a_2}, \cdots ,{a_n}]^{\rm{T}}}$ 构成的对角方阵。$ {\text{Re}}[ \cdot ] $ 表示给复数取实部操作符。$|\cdot|$ 表示取模操作符。$ \Vert \cdot {\Vert }_{2} $ 和$ \Vert \cdot {\Vert }_{\text{F}} $ 分别表示欧氏范数(Euclidean norm)和F范数(Frobenius norm)。其他符号在首次出现后定义。2. 问题建模与求解
2.1 系统模型
假设MIMO雷达系统由
$\hat L$ 个发射天线组成,令${{\bar {\boldsymbol{d}}}} = {\left[ {{{\bar d}_1},{{\bar d}_2}, \cdots ,{{\bar d}_{\hat L}}} \right]^{\text{T}}}$ 为阵列天线的位置向量,${\bar d_l}$ 表示第l个发射天线的位置,${x_l}(n),n = 1,2, \cdots ,N$ ,表示第l个天线发射的基带信号,$l = 1,2, \cdots ,\hat L$ ,其中N表示每个波形的离散采样点数。假设发射的探测信号是窄带的,那么方位向$\theta $ 处的信号可表示为[1-4]$$ \sum\limits_{l = 1}^{\hat L} {{{\text{e}}^{ - {{{\rm{j}}2\pi }}{f_0}\tau \bigr(\theta ,{{\bar d}_l}\bigr)}}} {x_l}(n) \triangleq {{\boldsymbol{c}}^{\text{H}}}(\theta ,{\boldsymbol{\bar d}}){\boldsymbol{x}}(n),\;n = 1,2, \cdots ,N $$ (1) 其中,
${\rm{j}} = \sqrt { - 1}$ ,${f_0}$ 为载波频率,$\tau (\theta ,{\bar d_l}) = {{\bar d}_l} \sin (\theta ) \mathord{\left/ {\vphantom {{{{\bar d}_l}\sin (\theta )} {\text{c}}}} \right. } {\text{c}}$ ,$ {\text{c}} $ 表示光速,$$ {\boldsymbol{x}}(n) = {\left[ {{x_1}(n),{x_2}(n), \cdots ,{x_{\hat L}}(n)} \right]^{\text{T}}} \in {\mathbb{C}^{\hat L \times 1}} $$ (2) $$ \begin{split} & {\boldsymbol{c}}(\theta ,{\boldsymbol{\bar d}}) = {\left[ {{{\text{e}}^{{{{\rm{j}}2\pi }}{f_0}\tau (\theta ,{{\bar d}_1})}},{{\text{e}}^{{{{\rm{j}}2\pi }}{f_0}\tau (\theta ,{{\bar d}_2})}}, \cdots ,{{\text{e}}^{{{{\rm{j}}2\pi }}{f_0}\tau (\theta ,{{\bar d}_{\hat{L} }})}}} \right]^{\text{T}}} \\ & \quad\in {\mathbb{C}^{\hat L \times 1}} \end{split} $$ (3) 假设MIMO雷达系统的发射天线已经过校准,即
${\boldsymbol{c}}(\theta ,{\boldsymbol{\bar d}})$ 是$\theta $ 和$ {\boldsymbol{\bar d}} $ 的确定函数,$\theta $ 方向上发射信号的功率(发射波束图)可表示为$$ P(\theta ) = {{\boldsymbol{c}}^{\text{H}}}(\theta ,{\boldsymbol{\bar d}}){\boldsymbol{X}}{{\boldsymbol{X}}^{\text{H}}}{\boldsymbol{c}}(\theta ,{\boldsymbol{\bar d}}) $$ (4) 其中,
$ {\boldsymbol{X}} \triangleq [{\boldsymbol{x}}(1),{\boldsymbol{x}}(2), \cdots, {\boldsymbol{x}}(N)] \in {\mathbb{C}^{\hat L \times N}} $ 。可以看到波束图表达式(4)是天线位置$\bar {\boldsymbol{d}}$ 和探测波形X的函数,因此可以通过优化天线位置$\bar {\boldsymbol{d}}$ 和探测波形X使雷达的辐射功率(波束图)指向特定的方向。为使雷达发射机工作效率最大化,通常要求雷达发射信号的幅度满足PAPR约束[12],对于探测波形矩阵X,其PAPR定义为信号幅度的峰值功率与平均功率之比[12,16,35,37]:
$$ {\text{PAPR}}({{\boldsymbol{X}}_{l,:}}) \triangleq \frac{{{{\max }_n}\left\{ {|{X_{l,n}}{|^2}} \right\}_{n = 1}^N}}{{\left\| {{{\boldsymbol{X}}_{l,:}}} \right\|_2^2/N}} \le {\zeta _l},\;l = 1,2, \cdots ,\hat L $$ (5) 其中,
${\zeta _l} \ge 1$ 表示给定的第l个发射波形的PAPR上界值。不失一般性,本文加入如下功率约束[33]:$$ \left\| {\boldsymbol{X}} \right\|_2^2 = \gamma $$ (6) 其中,
$\gamma $ 为雷达发射的总功率。2.2 天线选择
因天线位置变量
$\bar {\boldsymbol{d}}$ 位于天线阵列导向矢量${\boldsymbol{c}}(\theta ,{\boldsymbol{\bar d}})$ 的指数项中(见式(3)),直接建模对其进行优化十分复杂和困难。为使问题容易求解和处理,本文假设有L个离散的位置可用于天线放置(位置为$ {\bar d_1},{\bar d_2}, \cdots ,{\bar d_L} $ ),将优化位置转变为选择其中$\hat L \le L$ 个位置用于天线放置。基于此,定义天线位置选择向量${\boldsymbol{\bar s}} \in {\mathbb{R}^{L \times 1}}$ 满足$ {\bar s_l} \in \{ 0,1\} ,\forall l,{{\boldsymbol{\bar s}}^{\text{T}}}{{\bf{1}}} = \hat L $ ,即被选中的位置l对应${\bar s_l}$ 的值为1,反之则为0[47]。根据上述讨论与定义,波束图表达式(4)可等价为$$ P(\theta ) = {\left\| {{\boldsymbol{c}}_{}^{\text{H}}\left( \theta \right){\text{diag}}({\boldsymbol{\bar s}}){\boldsymbol{X}}} \right\|^2_2} $$ (7) 值得注意的是,由于假设可用天线位置和数量是已知的,因此导向矢量是已知的,此时
${\boldsymbol{c}}_{}^{\text{H}}(\theta ,{\boldsymbol{\bar d}})$ 退化为${\boldsymbol{c}}\left( \theta \right)$ 。将空间角$ [{0^\circ },{180^\circ }] $ 分成离散的点$\{ {\theta _m}\} _{m = 1}^M$ 。根据式(7)可得,离散角${\theta _m}$ 处的波束图为$$ {P_m} = \left\| {{\boldsymbol{c}}_m^{\text{H}}{\text{diag}}({\boldsymbol{\bar s}}){\boldsymbol{X}}} \right\|_2^2 $$ (8) 其中,
${{\boldsymbol{c}}_m} \triangleq {\boldsymbol{c}}({\theta _m})$ 。2.3 优化模型
在雷达应用中,雷达天线通常需要辐射多种不同的波束图(如波束扫描)以满足不同的探测任务[8-13]。集中式MIMO雷达可通过发射不同的探测波形实现发射波束的变化,但当集中式MIMO雷达系统使用稀疏天线阵时,传统的MIMO雷达发射波束图合成方法,如文献[1-5,8-13],因仅考虑ULA配置而无法满足设计要求,而现有基于天线选择的MIMO雷达波束图设计技术因为在设计中只考虑合成一个波束,如文献[14,16,19,29],在生成多个波束的应用场景中可能不是最优的。为此,本文在优化集中式MIMO雷达天线位置的同时优化多组探测波形集以保证集中式MIMO雷达的多波束变换能力。
假设集中式MIMO雷达需辐射I个波束图(对应的需产生I 组波形集,即
$\left\{ {{{\boldsymbol{X}}^i}} \right\}_{i = 1}^I$ ,${{\boldsymbol{X}}^i} \triangleq [{{\boldsymbol{x}}^i}(1),{{\boldsymbol{x}}^i}(2), \cdots, {{\boldsymbol{x}}^i}(N)] \in {\mathbb{C}^{L \times N}}$ ,每一个波形集合对应一个波束图)。根据式(8),本文构建如下天线位置选择和波形集联合优化问题以实现集中式MIMO雷达的波束扫描:$$ \begin{split} & \underset{{\{{{\boldsymbol{X}}}^{i},{\beta }^{i}\}}_{i=1}^{I},\bar{s}}{\mathrm{min}}\underset{i}{\mathrm{max}}\underset{m\in {{\boldsymbol{\varTheta}} }_{b}^{i}}{\mathrm{max}}\left\{{\tilde{w}}_{m}^{i}{\left({\beta }^{i}{d}_{m}^{i} - {\Vert {{\boldsymbol{c}}}_{m}^{\text{H}}\text{diag}(\bar{{\boldsymbol{s}}}){{\boldsymbol{X}}}^{i}\Vert }_{2}\right)}^{2}\right\}\\ & \quad \text{s}\text{.t}\text{. PAPR}({{\boldsymbol{X}}}_{l,:}^{i})\le {\zeta }_{l},\Vert {{\boldsymbol{X}}}_{l,:}^{i}{\Vert }_{2}^{2}=\gamma ,\forall l,\forall i;\\ & \qquad\quad\;\; {\bar{s}}_{l}\in \{0,1\},\forall l,{\bar{{\boldsymbol{s}}}}^{\text{T}}{{\boldsymbol{1}}}=\hat{L}\\[-10pt] \end{split} $$ (9) 其中,
$\tilde w_m^i$ 为用户给定的权重参数,可用来控制波束图主瓣波纹、旁瓣电平和零陷深度等,如文献[13]。${\boldsymbol{\varTheta}}_b^i \triangleq \{ {\boldsymbol{\varTheta}}_m^i,{\boldsymbol{\varTheta}}_s^i,{\boldsymbol{\varTheta}}_n^i\} $ ,其中${\boldsymbol{\varTheta}}_m^i,{\boldsymbol{\varTheta}}_s^i,{\boldsymbol{\varTheta}}_n^i$ 分别表示第i个波束图的主瓣区域、旁瓣区域和零陷区域,$ {\beta ^i} $ 和${{\boldsymbol{d}}^i} \in {\mathbb{C}^{{M^i} \times 1}}$ 分别表示第i个波束图对应缩放因子和波束图模板,其中${M^i}$ 表示${\boldsymbol{\varTheta}}_b^i$ 中的方位角离散点的个数,${\boldsymbol{\bar s}} \in {\mathbb{R}^{L \times 1}}$ 表示天线位置选择向量。2.4 算法推导
优化问题(9)的目标函数中的变量
$\{ {{\boldsymbol{X}}^i},{\beta ^i}\} _{i = 1}^I$ 和${\boldsymbol{\bar s}}$ 相互耦合,min-max运算导致了非光滑性。展开优化问题(9)的目标函数可得$$ \begin{split} & {\left( {{\beta ^i}d_m^i - {{\left\| {{\boldsymbol{c}}_m^{\text{H}}{\text{diag}}({\boldsymbol{\bar s}}){{\boldsymbol{X}}^i}} \right\|}_2}} \right)^2} \\ & \quad= {\left( {{\beta ^i}d_m^i} \right)^2} - 2{\beta ^i}d_m^i{\left\| {{\boldsymbol{c}}_m^{\text{H}}{\text{diag}}({\boldsymbol{\bar s}}){{\boldsymbol{X}}^i}} \right\|_2} \\ & \qquad + \left\| {{\boldsymbol{c}}_m^{\text{H}}{\text{diag}}({\boldsymbol{\bar s}}){{\boldsymbol{X}}^i}} \right\|_2^2 \end{split} $$ (10) 可见
$ - {\left\| {{\boldsymbol{c}}_m^{\text{H}}{\text{diag}}({\boldsymbol{\bar s}}){{\boldsymbol{X}}^i}} \right\|_2}$ 导致了式(9)目标函数的非凸性。此外,${\boldsymbol{\bar s}}$ 的可行域为离散的布尔类型点集合,变量${{\boldsymbol{X}}^i}$ 受限于非凸的PAPR约束。目标函数的非凸性和变量可行域的非凸性与不连续性使得优化问题(9)的求解十分困难。另外,随着波束图个数I、波形码长N、雷达系统发射天线$ \hat L $ 以及天线位置L的增加,优化问题(9)迅速趋于大规模,进一步增加了对优化问题(9)有效求解的难度。下面本文将针对优化问题(9)的上述难点一一给出相应的解决方案,并推导出该优化问题的有效求解算法。首先,引入辅助变量
$\{ {{\boldsymbol{Z}}^i}\} _{i = 1}^I$ 和${\boldsymbol{\alpha }} = [\alpha _1^{}, \alpha _2^{}, \cdots , \alpha _L^{}]^{\text{T}} \in {\mathbb{R}^{L \times 1}}$ ,并定义$$ {{\boldsymbol{Z}}^i} \triangleq {\text{diag}}({\boldsymbol{\bar s}}){{\boldsymbol{X}}^i},\forall i $$ (11) $$ \left\| {{\boldsymbol{X}}_{l,:}^i} \right\|_2^2 = \alpha _l^2,\forall l,\forall i $$ (12) 根据上述定义,优化问题(9)可写为如下等价的形式
$$ \begin{split} & \mathop {\min }\limits_{{\boldsymbol{\bar s}},{\boldsymbol{\alpha }},\{ {{\boldsymbol{X}}^i},{{\boldsymbol{Z}}^i},{\beta ^i}\} _{i = 1}^I} \mathop {\max }\limits_{\{ m,i\} } \left( {\tilde w_m^i{{\left( {{\beta ^i}d_m^i - {{\left\| {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|}_2}} \right)}^2}} \right) \\ & {\text{ s}}{\text{.t}}{\text{. }}{{\boldsymbol{Z}}^i} = {\text{diag}}({\boldsymbol{\bar s}}){{\boldsymbol{X}}^i},{\text{PAPR}}({\boldsymbol{X}}_{l,:}^i) \le {\zeta _l},\forall l,\forall i; \\ & \qquad \left\| {{\boldsymbol{X}}_{l,:}^i} \right\|_2^2 = \alpha _l^2,\forall l,\forall i;\left\| {\boldsymbol{\alpha }} \right\|_2^2 = \gamma ; \\ & \qquad {{\bar s}_l} \in \{ 0,1\} ,\forall l,{{{\boldsymbol{\bar s}}}^{\text{T}}}{{\bf{1}}} = \hat L \\[-10pt] \end{split} $$ (13) 可以看到,通过辅助变量的引入,优化问题(13)的目标函数中变量受限于线性约束
${{\boldsymbol{Z}}^i} = {\text{diag}}({\boldsymbol{\bar s}}){{\boldsymbol{X}}^i}$ ,而PAPR约束和布尔类型约束分别与变量${{\boldsymbol{X}}^i}$ 和${\boldsymbol{\bar s}}$ 相关。对于优化问题目标函数中的
$\max $ 操作和非凸问题,Lawson算法(参考文献[42,43,48])指出min-max优化问题的解可以通过求解一系列加权最小二乘问题获得。例如,针对优化问题
$$ \mathop {\min }\limits_x \mathop {\max }\limits_i {f_i}(x) $$ (14) Lawson算法通过迭代的方式求解,步骤如下:
步骤1 将min-max优化问题写为如下加权最小二乘问题,并求解该问题获得
$ x\left( t \right) $ :$$ x\left( t \right) = \arg \mathop {\min }\limits_x \sum\limits_i {{w_i}(t - 1){f_i}(x)} $$ (15) 步骤2 按如下规则更新权值
$$ {w_i}(t) = \frac{{{w_i}(t - 1){f_i}\bigr( {x\left( t \right)} \bigr)}}{{\displaystyle\sum\limits_i {{w_i}(t - 1){f_i}\bigr( {x\left( t \right)} \bigr)} }} $$ (16) 重复上述步骤,直至算法达到收敛条件。
下面根据Lawson算法处理优化问题(13)目标函数的非光滑性。首先,将优化问题(13)写为
$$ \begin{split} & \{ \{ {{\boldsymbol{X}}^i}(k),{{\boldsymbol{Z}}^i}(k),{\beta ^i}(k)\} _{i = 1}^I,{\boldsymbol{\alpha }}(k),{{\bar {\boldsymbol{s}}}}(k)\} \\ & \quad = \mathop {\arg \min }\limits_{\{ {{\boldsymbol{X}}^i},{{\boldsymbol{Z}}^i},{\beta ^i}\} _{i = 1}^I,{\boldsymbol{\alpha }},{{\bar {\boldsymbol{s}}}}} \sum\limits_{i = 1}^I {\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k)G_m^i({{\boldsymbol{Z}}^i},{\beta ^i})\\ & {\rm{s}}{\rm{.t}}{\rm{.}}\;{{\boldsymbol{Z}}^i} = {\rm{diag}}({{\bar {\boldsymbol{s}}}}){{\boldsymbol{X}}^i};{\rm{PAPR}}({\boldsymbol{X}}_{l,:}^i) \le {\zeta _l},\forall l,\forall i;\\ &\quad\;\; {{\bar s}_l} \in \{ 0,1\} ,\forall l,{{{{\bar {\boldsymbol{s}}}}}^{\rm{T}}} {{\boldsymbol{1}}} = \hat L;\left\|{\boldsymbol{X}}_{l,:}^i\right\|_2^2 = \alpha _l^2,\forall l,\forall i,\\ & \quad\left\|{\boldsymbol{\alpha }}\right\|_2^2 = \gamma \\[-10pt] \end{split} $$ (17) 其中,
$G_m^i({{\boldsymbol{Z}}^i},{\beta ^i}) \triangleq {\left( {{\beta ^i}d_m^i - {{\left\| {{\boldsymbol{c}}_m^{\rm{H}}{{\boldsymbol{Z}}^i}} \right\|}_2}} \right)^2}$ ,$$ \begin{split} & w_m^i(k) \\ & = \frac{{(w_m^i(k - 1) + \delta )\tilde w_m^iG_m^i({{\boldsymbol{Z}}^i}(k - 1),{\beta ^i}(k - 1))}}{{\displaystyle\sum\limits_{i = 1}^I {\displaystyle\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k - 1)\tilde w_m^iG_m^i({{\boldsymbol{Z}}^i}(k - 1),{\beta ^i}(k - 1))}},\\ & \forall i,\forall m\\[-10pt] \end{split} $$ (18) 为Lawson权值。从式(18)可以看到,当
$w_m^i(k - 1) = 0$ 时,$w_m^i(\bar k) = 0,\forall \bar k > k - 1$ ,为防止$w_m^i(k - 1) = 0$ 时导致的权值不更新的问题,设置$\delta $ 为一个很小的数,如${10^{ - 10}}$ 。定理1:令
${{\boldsymbol{Z}}^i}(t)$ 为变量${{\boldsymbol{Z}}^i}$ 在第t次迭代时的最优值,$$ {{\boldsymbol{d}}}_{m}^{i}(t+1)=\frac{{d}_{m}^{i}{{{\bar h}^{i}}}({{\boldsymbol{Z}}}^{i}(t)){{\boldsymbol{c}}}_{m}^{\text{H}}{{\boldsymbol{Z}}}^{i}(t)}{\Vert {{\boldsymbol{c}}}_{m}^{\text{H}}{{\boldsymbol{Z}}}^{i}(t){\Vert }_{2}}\in {\mathbb{C}}^{1\times N},\forall m,\forall i $$ (19) 其中,
$$ {\bar h^i}({{\boldsymbol{Z}}^i}) = \frac{{\displaystyle\sum\limits_{m = 1}^{{M^i}} {w_m^i} (k)d_m^i{{\left\| {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|}_2}}}{{\displaystyle\sum\limits_{m = 1}^{{M^i}} {w_m^i} (k){{(d_m^i)}^2}}},\forall i $$ 那么优化问题(17)的目标函数在点
${{\boldsymbol{Z}}^i} = {{\boldsymbol{Z}}^i}(t),\forall i$ 处的上界函数为$$ \begin{split} \tilde g(\{ {{\boldsymbol{Z}}^i},{{\boldsymbol{Z}}^i}(t)\} _{i = 1}^I) =& \sum\limits_{i = 1}^I {\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k)\\ & \cdot\left\| {{\boldsymbol{d}}_m^i(t + 1) - {\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|_2^2 + \omega \end{split} $$ (20) 其中,
$\omega$ 为常数。证明:
优化问题(17)的目标函数可写为
$$ \begin{split} & F\left( {\left\{ {{{\boldsymbol{Z}}^i},{\beta ^i},{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) \\ & \quad= \sum\limits_{i = 1}^I {\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k)G_m^i({{\boldsymbol{Z}}^i},{\beta ^i}) \\ & \quad= \sum\limits_{i = 1}^I {\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k){\left( {{\beta ^i}d_m^i - {{\left\| {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|}_2}} \right)^2} \end{split} $$ (21) 因为优化问题(17)是关于
${\beta ^i}$ 的无约束二次优化问题,令$ F\left( {\left\{ {{{\boldsymbol{Z}}^i},{\beta ^i},{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) $ 对${\beta ^i}$ 的导数等于零,则可得最优${\beta ^i}$ 与${{\boldsymbol{Z}}^i}$ 的关系为$$ {\beta ^i} = {\bar h^i}\left( {{{\boldsymbol{Z}}^i}} \right) = \dfrac{{\displaystyle\sum\limits_{m = 1}^{{M^i}} {w_m^i} (k)d_m^i{{\left\| {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|}_2}}}{{\displaystyle\sum\limits_{m = 1}^{{M^i}} {w_m^i} (k){{(d_m^i)}^2}}},\forall i $$ 即
$$ \begin{split} & \mathop {\min }\limits_{{\beta ^i}} F\left( {\left\{ {{{\boldsymbol{Z}}^i},{\beta ^i},{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) \\ & \quad = F\left( {\left\{ {{{\boldsymbol{Z}}^i},{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}} \right),{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) \end{split} $$ (22) 对于满足优化问题(17)的等式约束的任何
$ {{\boldsymbol{Z}}^i}(t),\forall i $ ,可得$$ \begin{split} & F\left( {\left\{ {{{\boldsymbol{Z}}^i},{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}} \right),{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) \\ & \quad\le F\left( {\left\{ {{{\boldsymbol{Z}}^i},{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right),{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) \end{split} $$ (23) 当
$ {{\boldsymbol{Z}}^i} = {{\boldsymbol{Z}}^i}(t),\forall i $ 时,等式成立。根据MM准则,式(22)和式(23)表明$F\left( \left\{ {{\boldsymbol{Z}}^i},{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right), {{\boldsymbol{Z}}^i}(t), {\beta ^i}(t) \right\} \right)$ 是$ F\left( {\left\{ {{{\boldsymbol{Z}}^i},{\beta ^i},{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) $ 的上界函数[13,49]。展开
$ F\left( {\left\{ {{{\boldsymbol{Z}}^i},{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right),{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) $ 可得$$ \begin{split} & F\left( {\left\{ {{{\boldsymbol{Z}}^i},{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right),{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right)\\ & \quad= \sum\limits_{i = 1}^I {\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k){\left( {{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right)d_m^i - {{\left\| {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|}_2}} \right)^2} \\ & \quad = \sum\limits_{i = 1}^I {\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k)\left( {{\left( {{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right)d_m^i} \right)}^2}\right.\\ & \qquad \left.- 2\left( {{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right)d_m^i{{\left\| {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|}_2}} \right) + \left\| {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|_2^2 \right) \\[-15pt] \end{split} $$ (24) 根据
${\left\| {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|_2} \ge \dfrac{{{{\rm{Re}}} \left[ {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}{{\left( {{{\boldsymbol{Z}}^i}(t)} \right)}^{\text{H}}}{\boldsymbol{c}}_m^{}} \right]}}{{{{\left\| {{\boldsymbol{c}}_m^{\rm{H}}{{\boldsymbol{Z}}^i}(t)} \right\|}_2}}}$ ,可得$$ \begin{split} & F\left( {\left\{ {{{\boldsymbol{Z}}^i},{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right),{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) \\ & \quad \mathop \le \limits_{} \sum\limits_{i = 1}^I {\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k) \Biggr( {{\left( {{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right)d_m^i} \right)}^2} \\ & \quad- 2\left( {{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right)d_m^i\frac{{{{\rm{Re}}} \left[ {{\boldsymbol{c}}_m^{\rm{H}}{{\boldsymbol{Z}}^i}{{\left( {{{\boldsymbol{Z}}^i}(t)} \right)}^{\text{H}}}{\boldsymbol{c}}_m^{}} \right]}}{{{{\left\| {{\boldsymbol{c}}_m^{\rm{H}}{{\boldsymbol{Z}}^i}(t)} \right\|}_2}}}} \right) \\ & \quad + \left\| {{\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|_2^2 \Biggr) \end{split} $$ (25) 消去式(25)右边常数项并配方,可得
$$ \begin{split} & F\left( {\left\{ {{{\boldsymbol{Z}}^i},{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right),{{\boldsymbol{Z}}^i}(t),{\beta ^i}(t)} \right\}} \right) \\ & \quad\le \sum\limits_{i = 1}^I {\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k)\left\| {{\boldsymbol{d}}_m^i(t + 1) - {\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|_2^2 + \omega \\ & \quad\triangleq \tilde g \left(\{ {{\boldsymbol{Z}}^i},{{\boldsymbol{Z}}^i}(t)\} _{i = 1}^I \right) \end{split} $$ (26) 由此可知,
$\tilde g(\{ {{\boldsymbol{Z}}^i},{{\boldsymbol{Z}}^i}(t)\} _{i = 1}^I)$ 为$F\left( \left\{ {{\boldsymbol{Z}}^i},{{\bar h}^i}\left( {{{\boldsymbol{Z}}^i}(t)} \right), {{\boldsymbol{Z}}^i}(t), {\beta ^i}(t) \right\} \right)$ 的上界函数。综上,定理1得证。证毕
根据MM算法原理[49-51],定理1表明优化问题(17)的解可通过求解如下优化问题得到
$$ \begin{split} & \underset{{\{{{\boldsymbol{X}}}^{i},{{\boldsymbol{Z}}}^{i}\}}_{i=1}^{I},{\boldsymbol{\alpha}} ,\bar{{\boldsymbol{s}}}}{\mathrm{min}}\tilde{g}(\{{{\boldsymbol{Z}}}^i,{\boldsymbol{Z}}^i(t)\}_{i=1}^{I})\\ & \text{ s}\text{.t}.\; {{\boldsymbol{Z}}}^{i}=\text{diag}(\bar{{\boldsymbol{s}}}){{\boldsymbol{X}}}^{i};\text{PAPR}({{\boldsymbol{X}}}_{l,:}^{i})\le {\zeta }_{l},\forall l,\forall i;\\ & \qquad \quad\; {\bar{s}}_{l}\in \{0,1\},\forall l,{\bar{{\boldsymbol{s}}}}^{\text{T}}{{\bf{1}}}=\hat{L};\\ & \qquad\quad\; \Vert {{\boldsymbol{X}}}_{l,:}^{i}{\Vert }_{2}^{2}={\alpha }_{l}^{2}, \forall l,\forall i,\Vert {\boldsymbol{\alpha}} {\Vert }_{2}^{2}=\gamma\\[-10pt] \end{split} $$ (27) 优化问题(27)的增广拉格朗日函数为
$$ \begin{split} & \mathcal{L}(\{ {{\boldsymbol{X}}^i},{{\boldsymbol{Z}}^i},{{\boldsymbol{\varPsi }}^i},{{\boldsymbol{Z}}^i}(t)\} _{i = 1}^I,{\boldsymbol{\alpha }},{\boldsymbol{\bar s}}) \\ & \quad= \tilde g(\{ {{\boldsymbol{Z}}^i},{{\boldsymbol{Z}}^i}(t)\} _{i = 1}^I) \\ & \qquad + \frac{\rho }{2}\sum\limits_{i = 1}^I {\left( {\left\| {{{\boldsymbol{Z}}^i} - {\text{diag}}({\boldsymbol{\bar s}}){{\boldsymbol{X}}^i} + {{\boldsymbol{\varPsi }}^i}} \right\|_{\text{F}}^2 - \left\| {{{\boldsymbol{\varPsi }}^i}} \right\|_{\text{F}}^2} \right)} \end{split} $$ (28) 根据ADMM优化框架[44-46],变量
$\{ \{ {{\boldsymbol{X}}^i},{{\boldsymbol{Z}}^i}, {{\boldsymbol{\varPsi }}^i}\} _{i = 1}^I,{\boldsymbol{\alpha }},{\boldsymbol{\bar s}}\}$ 的解可通过如下迭代步骤获得$$ \begin{split} & \{\{{{{\boldsymbol{X}}}^{i}}(t+1)\}^{I}_{i=1},\bar{{\boldsymbol{s}}}(t+1),{\boldsymbol{\alpha}} (t+1)\}\\ & \quad := {\arg}\;\underset{{{\boldsymbol{X}}}^{i},\bar{{\boldsymbol{s}}}}{\mathrm{min}}\mathcal{L}(\{{{{\boldsymbol{X}}}^{i}} ,{\boldsymbol{Z}}^i(t),{\boldsymbol{\varPsi}}^i(t)\}^I_{i=1},{\boldsymbol{\alpha }},\bar{{\boldsymbol{s}}})\\ & \quad\text{s}\text{.t}.\;{{\rm{PAPR}}}({{\boldsymbol{X}}}_{l,:}^{i})\le {\zeta }_{l},\Vert {{\boldsymbol{X}}}_{l,:}^{i}{\Vert }_{2}^{2}={\alpha }_{l}^{2},\forall l,\forall i;\\ & \qquad\;\;\; \Vert {\boldsymbol{\alpha}} {\Vert }_{2}^{2}=\gamma ;{\bar{{\boldsymbol{s}}}}_{l}\in \{0,1\},\forall l,{\bar{{\boldsymbol{s}}}}^{{\rm{T}}}{{{\bf{1}}}}=\hat{L}, \end{split} $$ (29) $$ \begin{split} \{ {{\boldsymbol{Z}}^i}(t + 1)\} _{i = 1}^I: = & \arg {\min _{{{\boldsymbol{Z}}^i}}}\mathcal{L}\bigr(\{ {{\boldsymbol{X}}^i}(t + 1),{{\boldsymbol{Z}}^i},{{\boldsymbol{\varPsi }}^i}(t)\} _{i = 1}^I,\\ & \{ {{\boldsymbol{Z}}^i}(t)\} _{i = 1}^I,{\boldsymbol{\alpha }}(t + 1),{\boldsymbol{\bar s}}(t + 1)\bigr) \end{split} $$ (30) $$ \begin{split} {{\boldsymbol{\varPsi }}^i}(t + 1): =& {{\boldsymbol{\varPsi }}^i}(t) + {{\boldsymbol{Z}}^i}(t + 1) \\ & - {\text{diag}}({\boldsymbol{\bar s}}(t + 1)){{\boldsymbol{X}}^i}(t + 1),\forall i \end{split} $$ (31) 本文用ADMM求解优化问题(17)对应的上界优化问题(27),而非直接利用ADMM求解(17),因此,将上述求解方法称为M-ADMM(感兴趣的读者请见文献[52])。下面给出优化问题(29)和(30)的求解方案。
2.4.1 优化问题(29)的求解
令
${{\boldsymbol{\bar Z}}^i} = {{\boldsymbol{Z}}^i}(t) + {{\boldsymbol{\varPsi }}^i}(t),\forall i$ ,并舍去优化问题(29)中的常数项,可得$$ \begin{split} & \underset{{\left\{{{\boldsymbol{X}}}^{i}\right\}}_{i=1}^{I},{\boldsymbol{\alpha}} ,\bar{{\boldsymbol{s}}}}{\mathrm{min}}{\displaystyle \sum _{i=1}^{I}{\Vert \text{diag}(\bar{{\boldsymbol{s}}}){{\boldsymbol{X}}}^{i}-{\bar{{\boldsymbol{Z}}}}^{i}\Vert }_{\text{F}}^{2}}\\ & \text{ s}\text{.t}.\;\text{PAPR}({{\boldsymbol{X}}}_{l,:}^{i})\le {\zeta }_{l},\Vert {{\boldsymbol{X}}}_{l,:}^{i}{\Vert }_{2}^{2}={\alpha }_{l}^{2},\forall l,\forall i;\\ & \qquad\; \Vert {\boldsymbol{\alpha}} {\Vert }_{2}^{2}=\gamma ;{\bar{s}}_{l}\in \{0,1\},\forall l,{\bar{{\boldsymbol{s}}}}^{\text{T}} {{\bf{1}}}=\hat{L} \end{split} $$ (32) 令
${\boldsymbol{x}}_l^i$ 和${\boldsymbol{\tilde z}}_l^i$ 分别表示变量${{\boldsymbol{X}}^i}$ 和${{\boldsymbol{\tilde Z}}^i}$ 的第l行,$x_{l,n}^i$ 表示${\boldsymbol{x}}_l^i$ 的第n个元素。优化问题(32)可写为如下形式:$$ \begin{split} & \underset{\left\{{{\boldsymbol{x}}}_{l}^{i}\right\},\bar{{\boldsymbol{s}}}}{\mathrm{min}}{\displaystyle \sum _{i=1}^{I}{\displaystyle \sum _{l=1}^{L}{\Vert {\bar{s}}_{l}{{\boldsymbol{x}}}_{l}^{i}-{\tilde{{\boldsymbol{z}}}}_{l}^{i}\Vert }_{2}^{2}}}\\ & \text{ s}\text{.t}\text{. }{\bar{s}}_{l}\in \{0,1\},\forall l,{\bar{{\boldsymbol{s}}}}^{\text{T}}{{\bf{1}}}=\hat{L};\Vert {\boldsymbol{\alpha}} {\Vert }_{2}^{2}=\gamma ;\\ & \qquad\quad N \mathop {\max }\limits_n \left\{{\left|{x}_{l,n}^{i}/{\Vert {{\boldsymbol{x}}}_{l}^{i}\Vert }_{2}\right|}^{2}\right\}\le {\zeta }_{l},\Vert {{\boldsymbol{x}}}_{l}^{i}{\Vert }_{2}^{2}={\alpha }_{l}^{2},\forall l,\forall i \end{split} $$ (33) 定义
${\bar{x}}_{l,n}^{i}={x}_{l,n}^{i}/\Vert {{\boldsymbol{x}}}_{l}^{i}{\Vert }_{2},\forall l,i,n$ ,可得$$ x_{l,n}^i = \bar x_{l,n}^i{\alpha _l},\forall l,i $$ (34) 将优化问题(33)的目标函数展开可得
$$ \begin{split} & \underset{\{{\bar{{\boldsymbol{x}}}}_{l}^{i}\},\bar{{\boldsymbol{s}}}}{\mathrm{min}}{\displaystyle \sum _{l=1}^{L} }{\displaystyle \sum _{i=1}^{I}\left({\bar{s}}_{l}^{2}{\alpha }_{l}^{2}-2{\bar{s}}_{l}{\alpha }_{l}^{}\text{Re}\left[{({\bar{{\boldsymbol{x}}}}_{l}^{i})}^{\text{H}}{\tilde{{\boldsymbol{z}}}}_{l}^{i}\right]+{\Vert {\tilde{{\boldsymbol{z}}}}_{l}^{i}\Vert }_{2}^{2}\right)}\\ & \text{s}\text{.t}\text{. }{\bar{s}}_{l}\in \{0,1\},\forall l,{\bar{{\boldsymbol{s}}}}^{\text{T}}{{\bf{1}}}=\hat{L};\Vert {\boldsymbol{\alpha}} {\Vert }_{2}^{2}=\gamma ;\\ & \quad\;\; N \mathop {\max }\limits_n |{\bar{x}}_{l,n}^{i}{|}^{2}\le {\zeta }_{l},\Vert {\bar{{\boldsymbol{x}}}}_{l}^{i}{\Vert }_{2}^{2}=1,\forall l,\forall i \\[-15pt] \end{split} $$ (35) (1) 求解
${\boldsymbol{\bar x}}_l^i(t + 1)$ :可以看到变量
${\boldsymbol{\bar x}}_l^i$ 的最优解与${\boldsymbol{\bar s}}$ 无关[43],因此,忽略掉无关项,优化问题(35)可简化为$$ \begin{split} & \underset{{\bar{{\boldsymbol{x}}}}_{l}^{i}}{\mathrm{max}}\text{ Re}[{(}{{\bar{{\boldsymbol{x}}}}_{l}^{i}}{\tilde{{\boldsymbol{z}}}}_{l}^{i}]\\ & \text{s}\text{.t}\text{. }N|{\bar{x}}_{l,n}^{i}{|}^{2}\le {\zeta }_{l},\forall n;\Vert {\bar{{\boldsymbol{x}}}}_{l}^{i}{\Vert }_{2}^{2}=1 \end{split} $$ (36) 其中,
$i = 1, 2,\cdots ,I,\;l = 1, 2,\cdots ,L$ 。对于每一个i和l,优化问题(36)可以用Nearest-Vector算法以分布式的方式有效的求解(见文献[53])。(2) 求解
${\boldsymbol{\bar s}}(t + 1),{\boldsymbol{\alpha }}(t + 1)$ :获得
${\boldsymbol{\bar x}}_l^i(t + 1),\forall l,\forall i$ 后,${\boldsymbol{\bar s}}\left( {t + 1} \right)$ 的解可通过求解如下优化问题获得(注:变量${\boldsymbol{\bar s}}$ 的可行域使得${\boldsymbol{\bar s}}$ 满足$\hat L$ 个元素为1,其他剩余元素值为0,且${{\boldsymbol{\bar s}}^{\rm{T}}}{\boldsymbol{\bar s}} = \hat L$ ):$$ \begin{split} & \underset{\bar{{\boldsymbol{s}}},{\boldsymbol{\alpha}} }{\mathrm{min}}\hat{L}\gamma -2{\displaystyle \sum _{l=1}^{L}{\alpha }_{l}^{}{\bar{s}}_{l}}{\displaystyle \sum _{i=1}^{I}{\tilde{r}}_{l}^{i}}+{\displaystyle \sum _{i=1}^{I}{\displaystyle \sum _{l=1}^{L}\Vert {\tilde{{\boldsymbol{z}}}}_{l}^{i}{\Vert }_{2}^{2}}}\\ & \text{s}\text{.t}\text{. }{\bar{s}}_{l}\in \{0,1\},\forall l,{\bar{{\boldsymbol{s}}}}^{\text{T}}{{\bf{1}}}=\hat{L};\Vert {\boldsymbol{\alpha}} {\Vert }_{2}^{2}=\gamma \end{split} $$ (37) 其中,
$\tilde r_l^i \triangleq {\text{Re}}[{({\boldsymbol{\bar x}}_l^i)^{\rm{H}}}{\boldsymbol{\tilde z}}_l^i]$ ,忽略常数项可得$$ \begin{split} &\underset{\bar{{\boldsymbol{s}}},{\boldsymbol{\alpha}} }{\mathrm{min}} -2{\displaystyle \sum _{l=1}^{L}{\bar{s}}_{l}}{\tilde{\tilde{r}}}_{l}\text{ }\\ & \text{s}\text{.t}\text{. } {\bar{s}}_{l}\in \{0,1\},\forall l,{\bar{{\boldsymbol{s}}}}^{\text{T}} {{\bf{1}}}=\hat{L},\Vert {\boldsymbol{\alpha}} {\Vert }_{2}^{2}=\gamma \end{split} $$ (38) 其中,
${\tilde {\tilde r}_l} = \displaystyle\sum\limits_{i = 1}^I {\tilde r_l^i}$ 。若$ {\varrho _1}, \cdots ,{\varrho _{\hat L}}, \cdots ,{\varrho _L} $ 表示集合$\{ {\tilde {\tilde r}_l}\}$ 的降序序列,那么${\boldsymbol{\bar s}}(t + 1)$ 的值为$$ {\bar{s}}_{l}(t+1)=\left\{\begin{aligned} &1, {\tilde{\tilde{r}}}_{l}\ge {\varrho }_{\hat{L}} \\ &0, 其他 \end{aligned},\;l=1,2,\cdots ,L \right. $$ (39) 将
${\bar s_l}(t + 1)$ 代入式(35)可得关于的$ {\boldsymbol{\alpha }} $ 二次优化问题,求解可得$$ {\boldsymbol{\alpha }}(t + 1) = \sqrt \gamma {\text{diag}}\left( {{{{\boldsymbol{\bar s}}}^{\text{T}}}(t + 1)} \right)\tilde {\tilde {\boldsymbol{r}}}{\left\| {{\text{diag}}({\boldsymbol{\bar s}})\tilde {\tilde {\boldsymbol{r}}}} \right\|_2} $$ (40) 根据式(34)和式(36)可得
${{\boldsymbol{X}}^i}(t + 1)$ 的解。2.4.2 优化问题(30)的求解
令
${\tilde {\boldsymbol{\varPsi }}^i} = {\rm{diag}}({\boldsymbol{\bar s}}(t + 1)){\text{ }}{{\boldsymbol{X}}^i}(t + 1) - {{\boldsymbol{\varPsi }}^i}(t),\forall i$ ,并忽略式(30)中的常数项可得$$ \begin{split} & \mathop {\min }\limits_{\{ {{\boldsymbol{Z}}^i}\} _{i = 1}^I} \sum\limits_{i = 1}^I {\sum\limits_{m = 1}^{{M^i}} {w_m^i} } (k)\left\| {{\boldsymbol{d}}_m^i(t + 1) - {\boldsymbol{c}}_m^{\text{H}}{{\boldsymbol{Z}}^i}} \right\|_2^2 \\ & \quad + \frac{\rho }{2}\sum\limits_{i = 1}^I {\left\| {{{\tilde {\boldsymbol{\varPsi }}}^i} - {{\boldsymbol{Z}}^i}} \right\|_{\text{F}}^2} \end{split} $$ (41) 令
$$ \quad {{\boldsymbol{C}}^i} = [{{\boldsymbol{c}}_1},{{\boldsymbol{c}}_2}, \cdots ,{{\boldsymbol{c}}_{{M^i}}}] \in {\mathbb{C}^{L \times {M^i}}} $$ $$ \quad{{\boldsymbol{w}}^i} = [w_1^i(k),w_2^i(k), \cdots ,w_{{M^i}}^i(k)]^{\rm{T}} \in {\mathbb{C}^{{M^i} \times 1}} $$ $$ \quad {{\boldsymbol{D}}^i} = [{\boldsymbol{d}}_1^i(t + 1),{\boldsymbol{d}}_2^i(t + 1), \cdots ,{\boldsymbol{d}}_{{M^i}}^i(t + 1)] \in {\mathbb{C}^{{M^i} \times N}} $$ 根据
${{\boldsymbol{C}}^i}$ 和${{\boldsymbol{D}}^i}$ 的定义,可将式(41)写为如下紧凑的形式:$$ \begin{split} & \mathop {\min }\limits_{{{\boldsymbol{Z}}^i}} \left\| {{\text{diag}}\left( {\sqrt {{{\boldsymbol{w}}^i}} } \right)\left( {{{\boldsymbol{D}}^i} - {{({{\boldsymbol{C}}^i})}^{\text{H}}}{{\boldsymbol{Z}}^i}} \right)} \right\|_{\text{F}}^2 \\ & \quad + \frac{\rho }{2}\left\| {{{\tilde {\boldsymbol{\varPsi }}}^i} - {{\boldsymbol{Z}}^i}} \right\|_{\text{F}}^2,\forall i \end{split} $$ (42) 进而有
$$ \begin{split} & \mathop {\min }\limits_{{\boldsymbol{z}}_n^i} \left\| {{\text{diag}}\left( {\sqrt {{{\boldsymbol{w}}^i}} } \right)\left( {\tilde {\boldsymbol{d}}_n^i - {{({{\boldsymbol{C}}^i})}^{\text{H}}}{\boldsymbol{z}}_n^i} \right)} \right\|_2^2 \\ & \quad + \frac{\rho }{2}\left\| {\tilde {\boldsymbol{\psi }}_n^i - {\boldsymbol{z}}_n^i} \right\|_2^2,\forall i,\forall n \end{split} $$ (43) 其中,
$\tilde {\boldsymbol{d}}_n^i$ ,${\boldsymbol{z}}_n^i$ 以及$\tilde {\boldsymbol{\varPsi }}_n^i$ 分别表示${{\boldsymbol{D}}^i}$ ,${{\boldsymbol{Z}}^i}$ 和${\tilde {\boldsymbol{\varPsi }}^i}$ 的第n列。易得优化问题(43)的解为$$ \begin{split} {\boldsymbol{z}}_n^i =& {\left( {{{\boldsymbol{C}}^i}{\text{diag}}({{\boldsymbol{w}}^i}){{({{\boldsymbol{C}}^i})}^{\text{H}}} + (\rho /2){{\boldsymbol{I}}_L}} \right)^{ - 1}}\\ & \cdot\left( {{{\boldsymbol{C}}^i}{\text{diag}}({{\boldsymbol{w}}^i})\tilde {\boldsymbol{d}}_n^i + (\rho /2)\tilde {\boldsymbol{\psi }}_n^i{\text{ }}} \right),\forall n,\forall i \end{split} $$ (44) 适当整理式(44),可得
$$ \begin{split} {{\boldsymbol{Z}}^i}(t + 1) =& {\left( {{{\boldsymbol{C}}^i}{\text{diag}}({{\boldsymbol{w}}^i}){{({{\boldsymbol{C}}^i})}^{\text{H}}} + (\rho /2){{\boldsymbol{I}}_L}} \right)^{ - 1}}\\ & \cdot\left( {{{\boldsymbol{C}}^i}{\text{diag}}({{\boldsymbol{w}}^i}){{\boldsymbol{D}}^i} + (\rho /2){{\tilde {\boldsymbol{\varPsi }}}^i}{\text{ }}} \right),\forall i \end{split} $$ (45) 表1总结了本文算法的流程。
表 1 基于波形优化和天线位置选择的MIMO雷达波束扫描算法Table 1. Algorithm for joint waveform optimization and antenna position selection for MIMO radar beam scanning输入参数:I, ${\boldsymbol{\varTheta }}_m^i$, ${\boldsymbol{\varTheta }}_s^i$, ${\boldsymbol{\varTheta }}_n^i$, ${\boldsymbol{\varTheta }}_t^i$, ${{\boldsymbol{W}}^i},\forall i$, ${\zeta _l},\forall l$, $\gamma $, $\hat L$, L, $\rho $, ${\delta _{{\rm{out}}} } = {10^{ - 8} }$, ${\delta _{{\rm{inner}}} } = {10^{ - 8} }$,
$\{ \{ {{\boldsymbol{X}}^i}(0),{{\boldsymbol{Z}}^i}(0),{{\boldsymbol{\varPsi }}^i}(0)\} _{i = 1}^I,{\boldsymbol{\alpha }}(0),{\boldsymbol{\bar s}}(0)\} $, $\tilde R_{m,q}^i(0) = W_{m,q}^i\left[ {{{\boldsymbol{W}}^i}; \cdots ;{{\boldsymbol{W}}^I}} \right]$, $\forall i,\forall m,\forall q$, ${K_{{\rm{max}}} }$, $k = 0$。1 WHILE {$|{\rm{obj}}(k) - {\rm{obj}}(k - 1)| > {\sigma _{{\rm{out}}} }$ & $k \le {K_{ {\rm{max} } } }$}(Lawson迭代) 2 $t = 0$;
3 WHILE $\left\{ {\dfrac{1}{I}\displaystyle\sum\limits_{i = 1}^I {\left\| { { {\boldsymbol{Z} }^i}(t) - { {\boldsymbol{Z} }^i}(t - 1)} \right\|_{\rm F}^2} > {\sigma _{{\rm{inner}}} } } \right\}$(M-ADMM迭代)4 $ \bullet $ 更新${\boldsymbol{d}}_m^i(t + 1)$; 5 $ \bullet $ 顺序更新$\{ {\boldsymbol{\bar s}}(t + 1),{\boldsymbol{\alpha }}(t + 1),\{ {{\boldsymbol{X}}^i}(t + 1)\} _{i = 1}^I\} $; 6 $ \bullet $ 更新$\{ {{\boldsymbol{Z}}^i}(t + 1)\} _{i = 1}^I$; 7 $ \bullet $ 更新$\{ {{\boldsymbol{\varPsi }}^i}(t + 1)\} _{i = 1}^I$; 8 $t: = t + 1$; 9 ENDWHILE(M-ADMM迭代结束) 10 ${{\boldsymbol{Z}}^i}(k + 1) = {{\boldsymbol{Z}}^i}(t - 1),\forall i,{\beta ^i}(k + 1) = {\bar h^i}({{\boldsymbol{Z}}^i}(k + 1)),\forall i$; 11 更新Lawson权值$w_m^i(k)$; 12 ${\rm{obj}}(k) = {\max _{m,i} }\{ G_m^i({ {\boldsymbol{Z} }^i}(k + 1),{\beta ^i}(k + 1))\}$; 13 $k: = k + 1$; 14 ENDWHILE(Lawson迭代结束) 输出:探测波形${{\boldsymbol{Z}}^i}( \star ) = {{\boldsymbol{Z}}^i}(t),i = 1,2,\cdots,I$,天线位置${\boldsymbol{\bar s}}( \star ) = {\boldsymbol{\bar s}}(t)$。 3. 复杂度分析
表1中第4、第5行主要运算是矩阵与向量乘法以及向量元素相除,复杂度为
$\mathcal{O}\Bigr( \displaystyle\sum\nolimits_{i = 1}^I {M^i}N{L^2} + LN + 4{M^i} \Bigr)$ 。算法第6行主要运算为矩阵乘法,复杂度为$\mathcal{O}\left( {\displaystyle\sum\nolimits_{i = 1}^I {{L^3} + {L^3}N + LN{{({M^i})}^2}} } \right)$ 。更新Lawson权值需要计算$G_m^i({{\boldsymbol{Z}}^i},{\beta ^i})$ ,主要运算是矩阵和向量乘法,复杂度为$\mathcal{O}\displaystyle\sum\nolimits_{i = 1}^I {({M^i}N{L^2} + LN)}$ 。综上,本文算法的整体复杂度为$\mathcal{O}\Bigr[ \tilde K\Bigr( \displaystyle\sum\nolimits_{i = 1}^I \Bigr( {M^i}N{L^2} + LN + \tilde T\bigr( {{M^i}N{L^2} + {L^3} + {L^3}N + LN{{({M^i})}^2} + LN + 4{M^i}} \bigr) \Bigr) \Bigr) \Bigr]$ ,其中$\tilde K$ 和$\tilde T$ 分别表示算法达到收敛所需的外迭代次数和内迭代次数。4. 仿真实验
本节通过仿真样例验证本文方法的有效性。除非另有说明,仿真参数设置如下:空间方位角
$[{0^\circ },{180^\circ }]$ 被分成181个离散点,即采样间隔为1°;变量的初始值,即$\{ \{ {{\boldsymbol{X}}^i}(0),{{\boldsymbol{Z}}^i}(0),{{\boldsymbol{\varPsi }}^i}(0)\} _{i = 1}^I\}$ ,以随机数的方式给定;另外,${\beta ^i} = 1,\forall i$ ,${\bar s_l}(0) = 1,\forall l$ ,${\sigma _{{\rm{out}}}} = {10^{ - 10}},\;{K_{{\rm{max}}}} = 2000,\;{\sigma _{{\rm{inner}}}} = {10^{ - 6}},{\zeta _l} = 1.5,\;\forall l$ ,$\gamma = 1,\alpha _l^{} = \sqrt {\gamma/L} ,N = 32$ ;此外,假设天线可选择的位置数$L = 20$ ,间距为半波长$\bar d = {\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. } 2} = {{\rm{c}} \mathord{\left/ {\vphantom {v {2{f_c}}}} \right. } ({2{f_c}})}$ ,天线数$\hat L = 12$ 。以下4个仿真例子验证了本文算法的有效性。
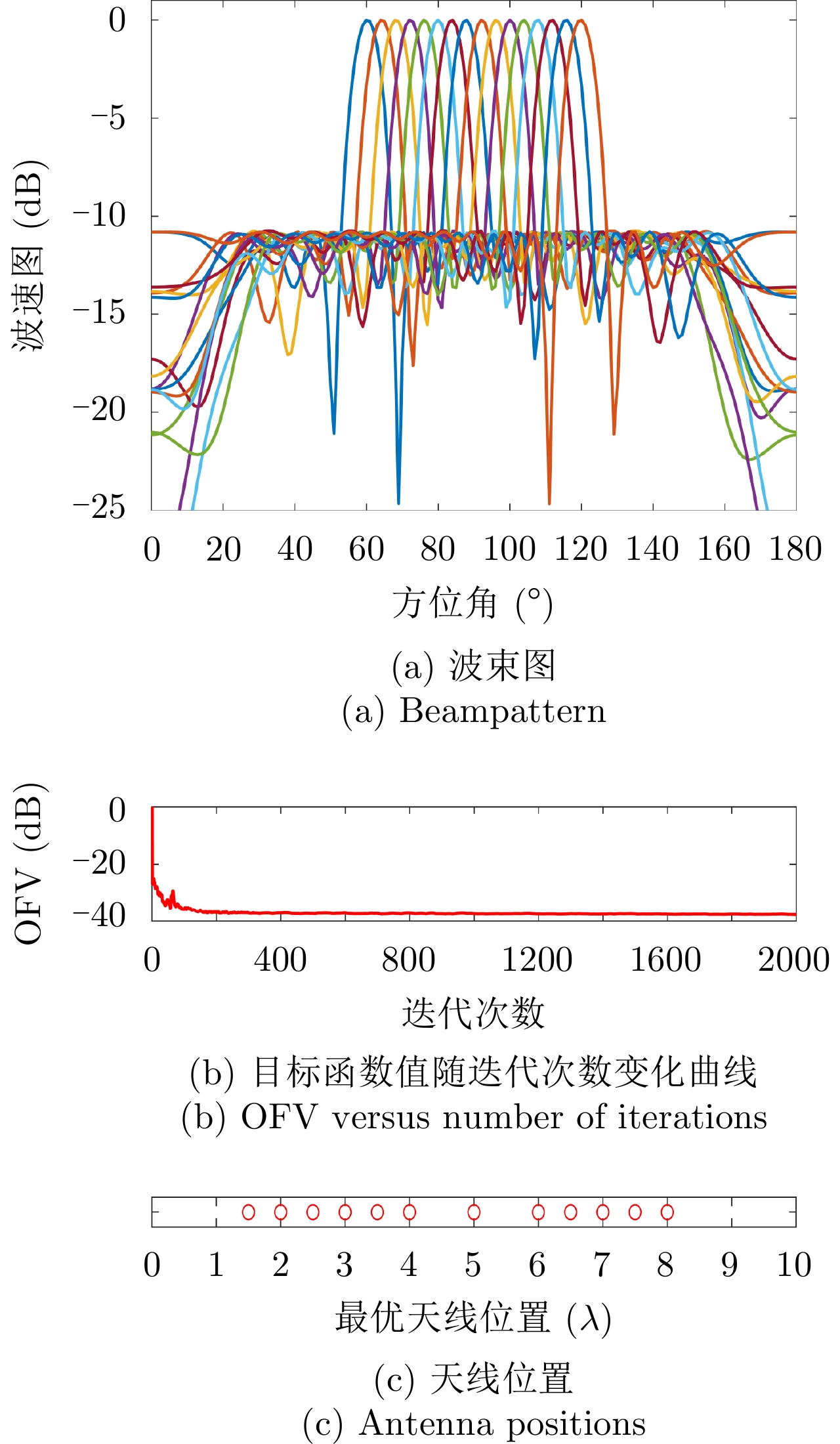
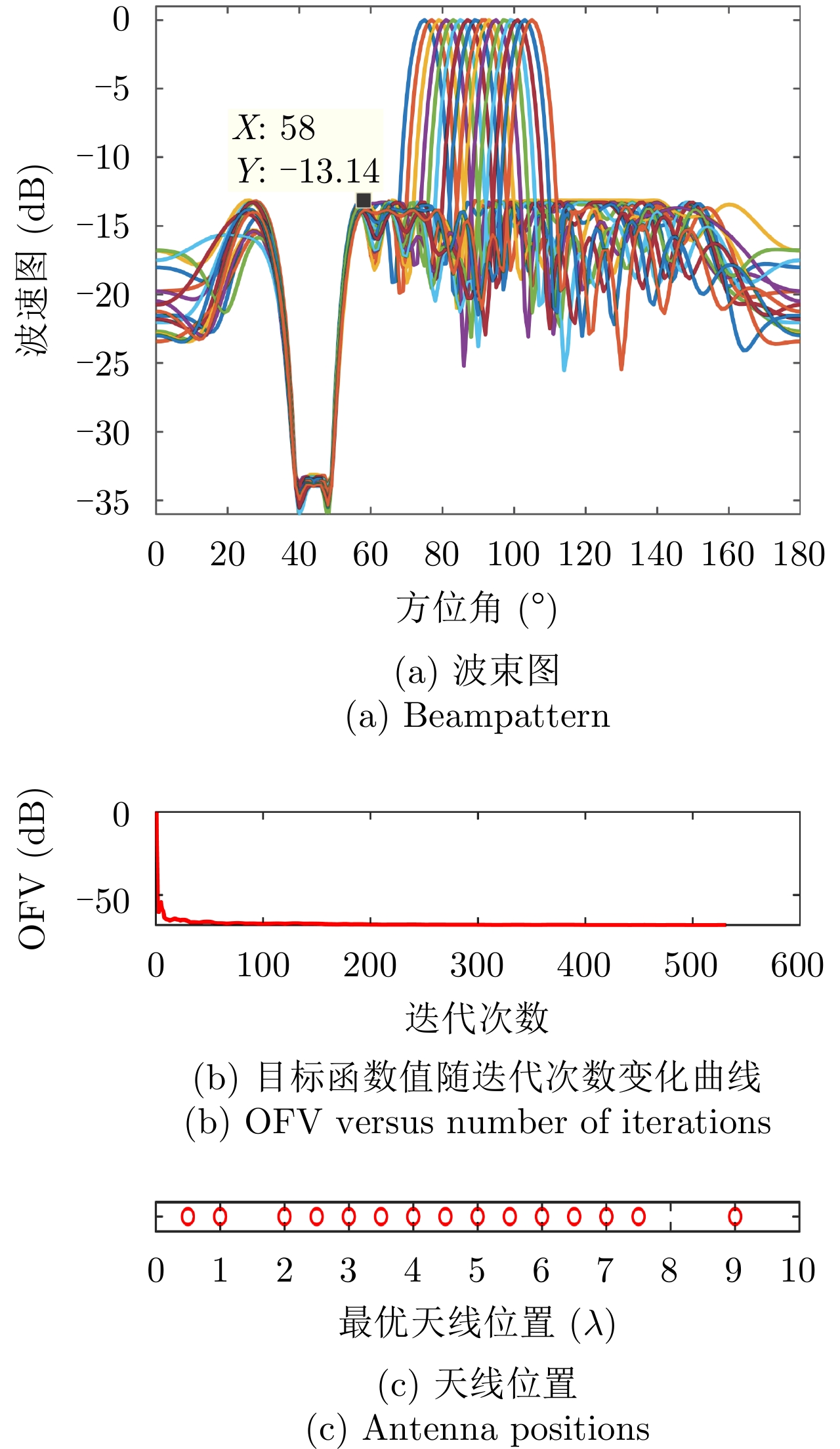
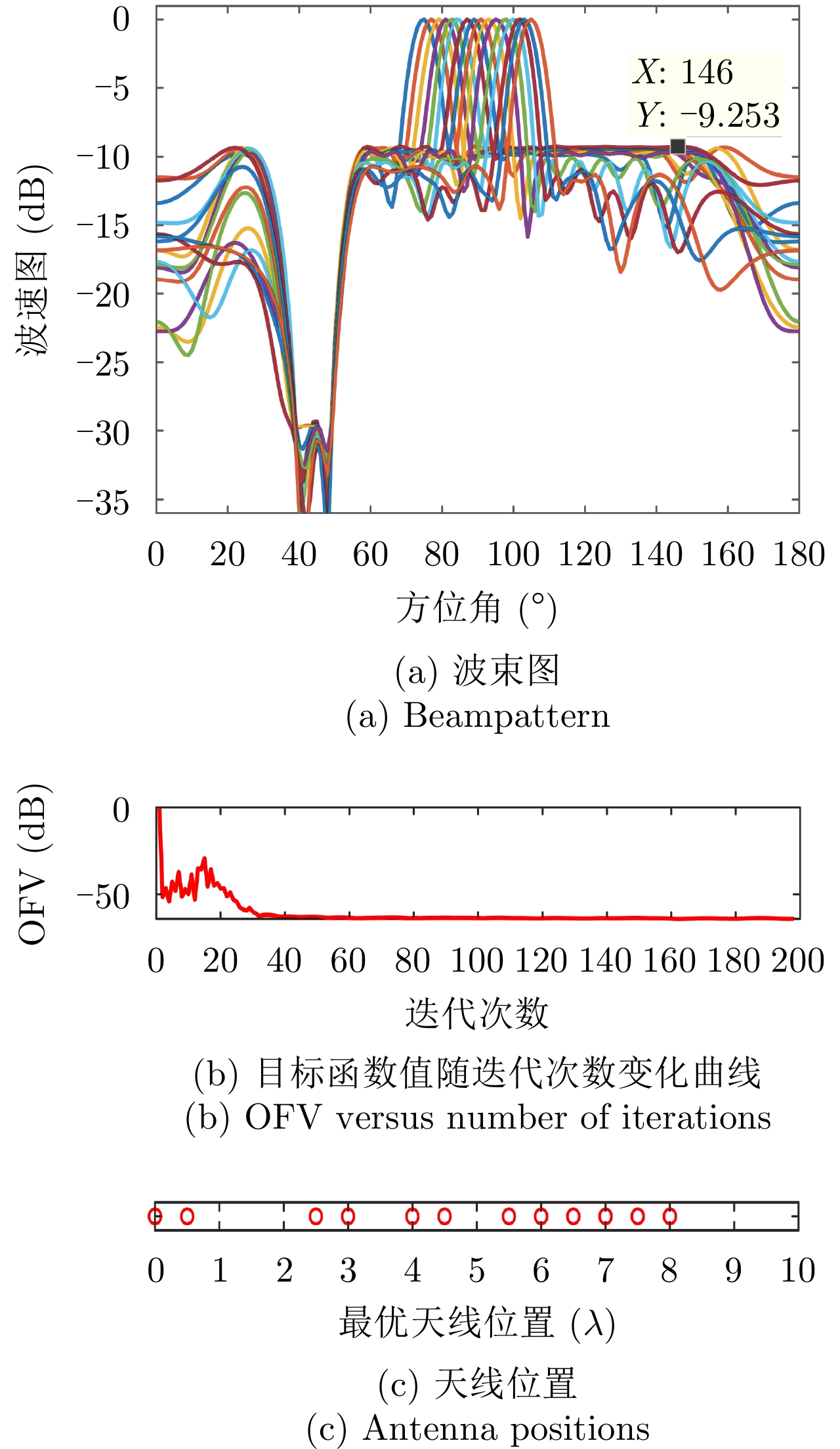
样例 1:稀疏天线阵列有16种不同的束状波束,即
$I = 16$ ,${\boldsymbol{\varTheta }}_m^i = {60^\circ } + (i - 1){4^\circ },i = 1,2, \cdots ,I$ ,${\boldsymbol{\varTheta }}_t^i \in \left[ {{\boldsymbol{\varTheta }}_m^i - {6^\circ },{\boldsymbol{\varTheta }}_m^i - {1^\circ }} \right] \cup \left[ {{\boldsymbol{\varTheta }}_m^i + {1^\circ },{\boldsymbol{\varTheta }}_m^i + {6^\circ }} \right],\forall i$ ,${\boldsymbol{\varTheta }}_n^i \in \varnothing ,\forall i$ ,其余的设为旁瓣区域,即${\boldsymbol{\varTheta }}_s^i,\forall i$ 。图1(a)—图1(c)分别给出了波束图合成结果、优化问题目标函数值(Objective Function Value, OFV)随算法迭代次数的变化曲线以及最优天线位置结果;从图1(a)可以看到16个波束图具有几乎相同的波束图旁瓣水平,且每个波束图的旁瓣水平几乎相等,表明了本文min-max设计准则的有效性;从图1(b)可以看到,经过大约200次迭代后,目标函数值几乎保持不变,算法收敛;从图1(c)可以看到,优化后天线单元的位置已经不再是等间距的,具有稀疏结构。
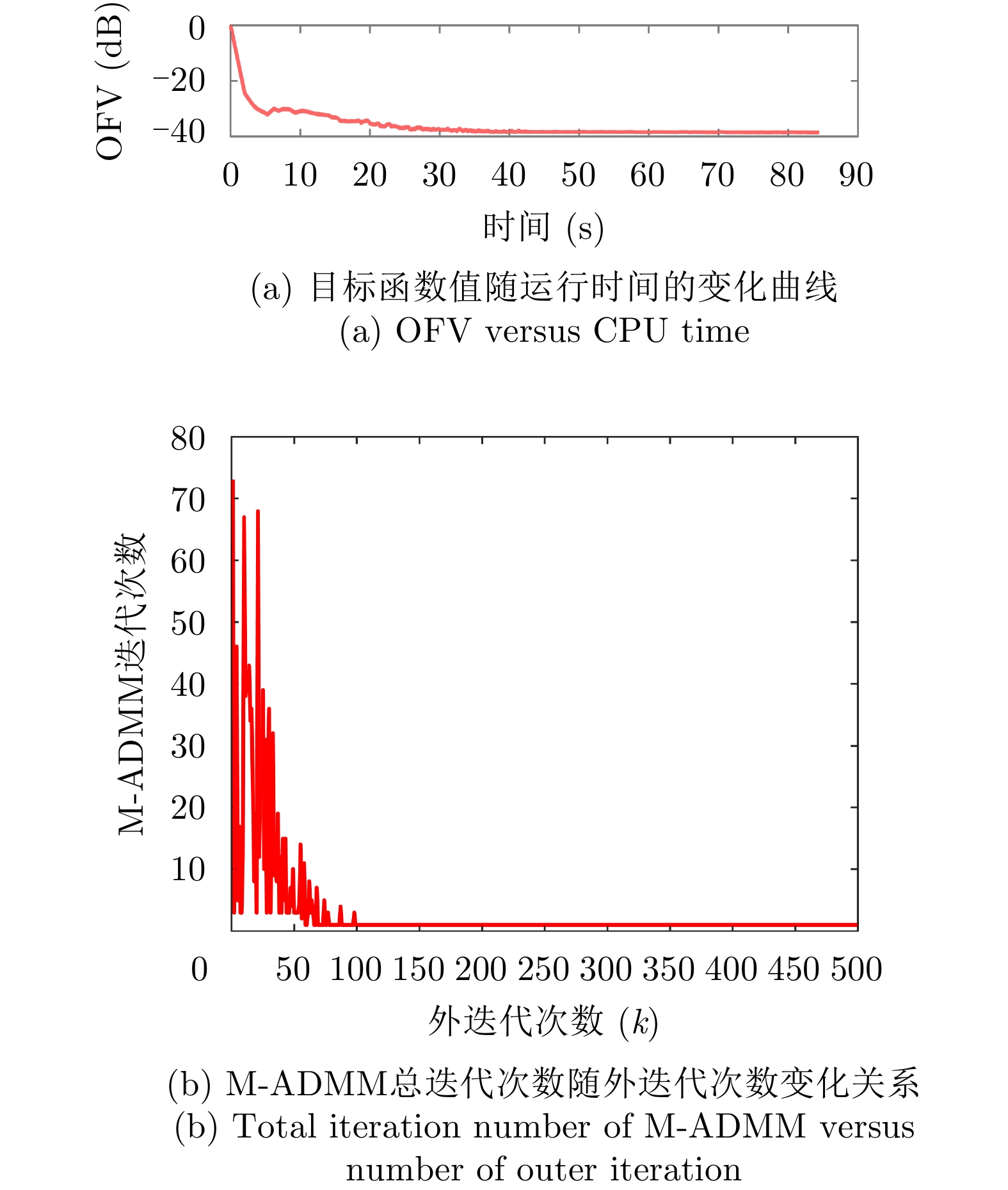
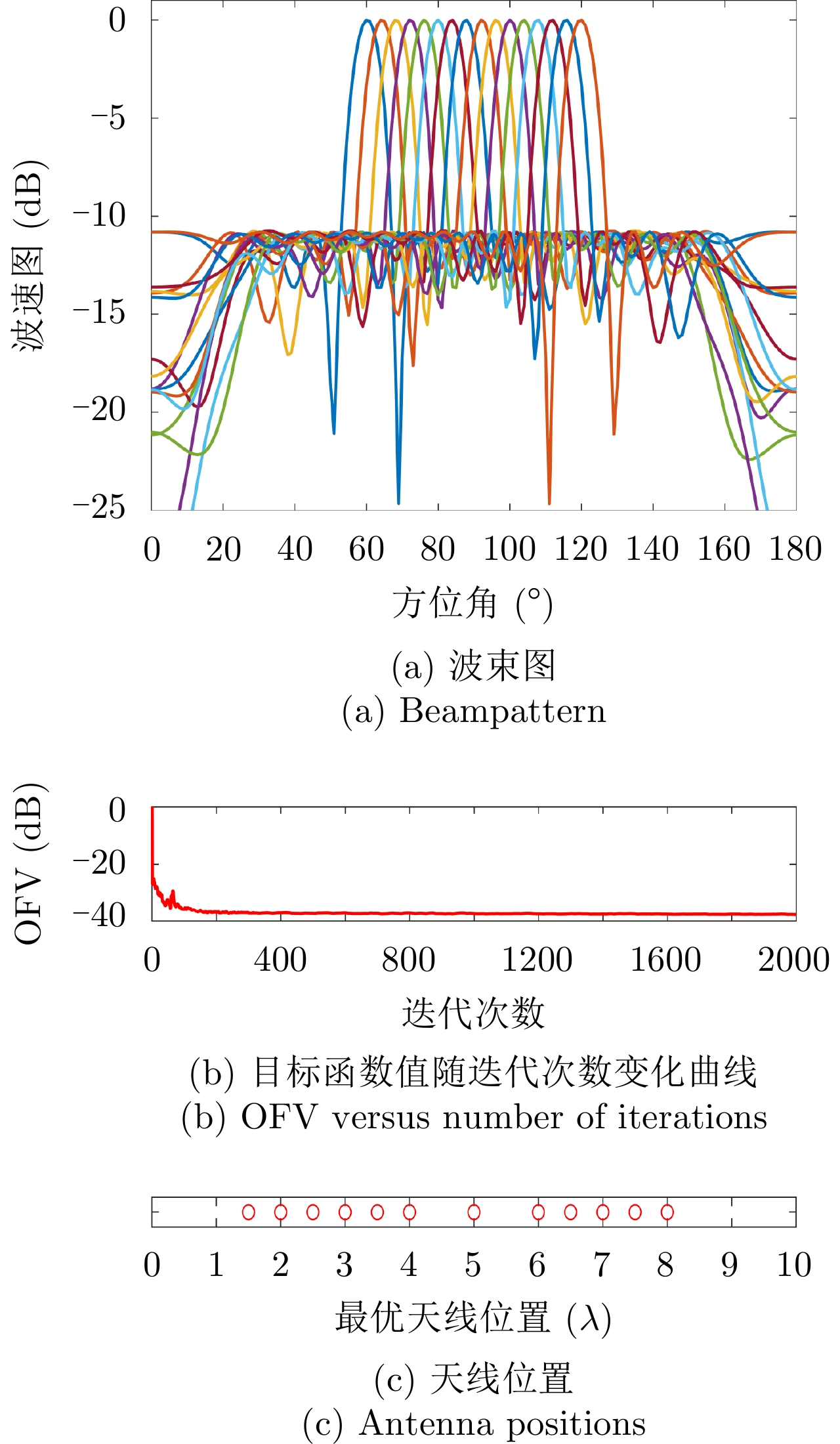
图2(a)和图2(b)分别绘制了样例1中目标函数值随算法运行时间的变化曲线以及M-ADMM迭代总次数和算法外迭代次数的变化关系,由图2(a)可以看到大约40秒后目标函数值基本保持不变,算法达到收敛。图2(b)可以看到随着外迭代次数的增加,M-ADMM迭代的次数也趋于减小(从最大73次,逐渐减少到1次),并且最后保持到仅需1次迭代。结合图1(b)和图2(b)结果可以看到随着迭代进行算法逐渐收敛,且算法内迭代次数也趋于减少,大约200次外迭代后算法收敛。图2结果表明,虽然本文算法单次迭代复杂度较高,但M-ADMM的快速收敛性使得本文算法在实际中依然有很好的实用性。
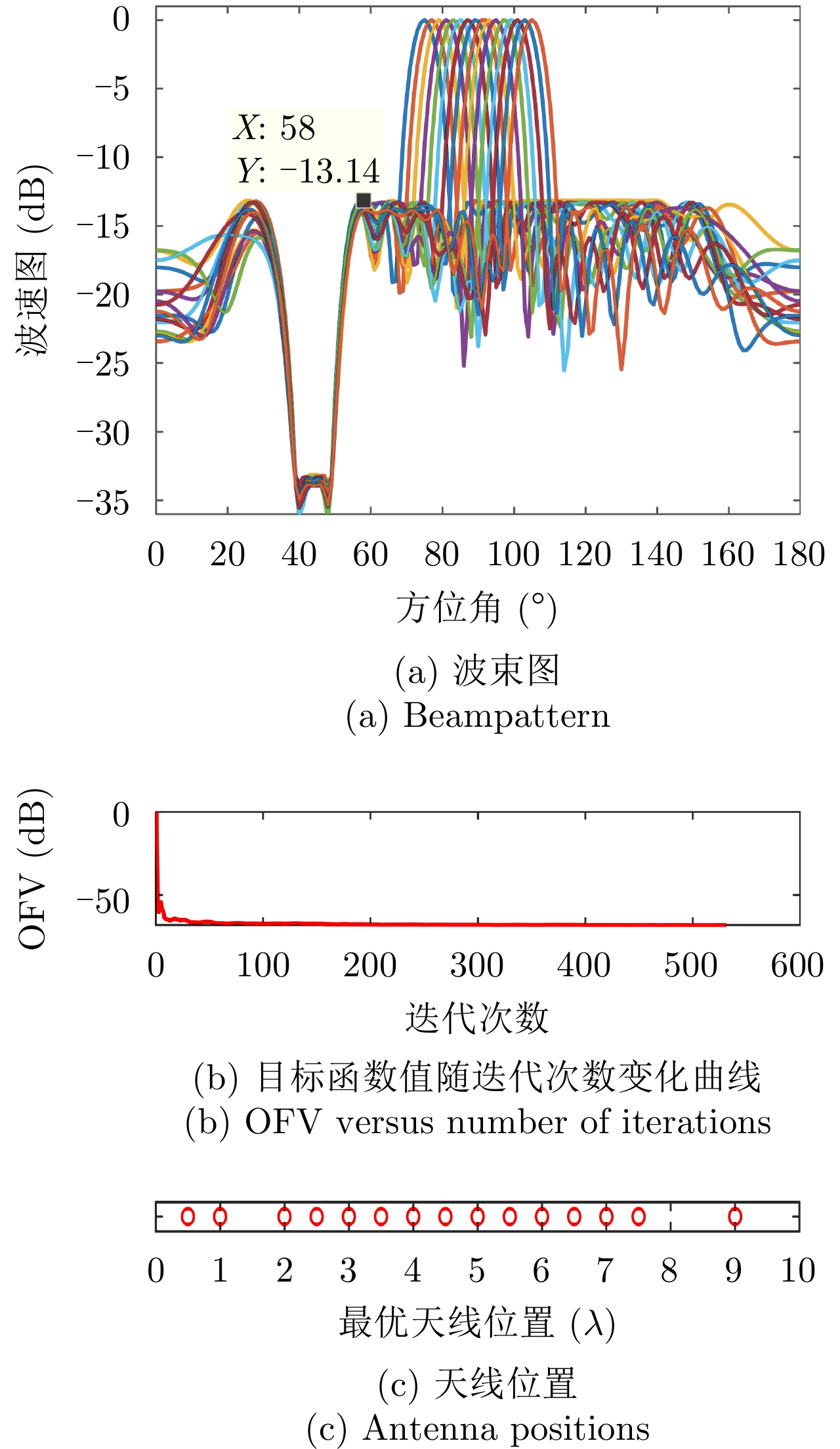
样例 2:稀疏天线阵列有16种不同的束状波束,且所有波束具有比峰值旁瓣图水平低
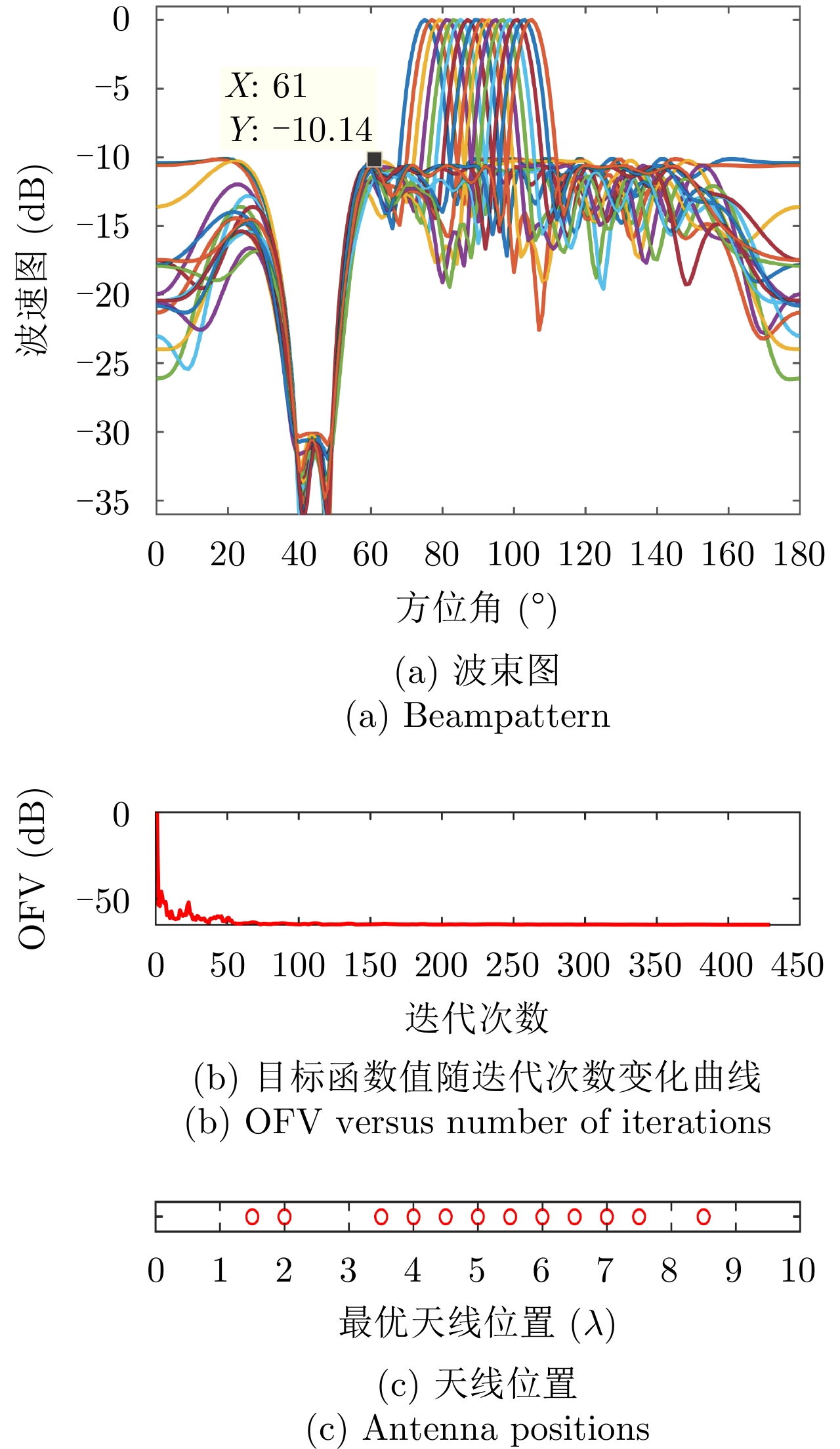
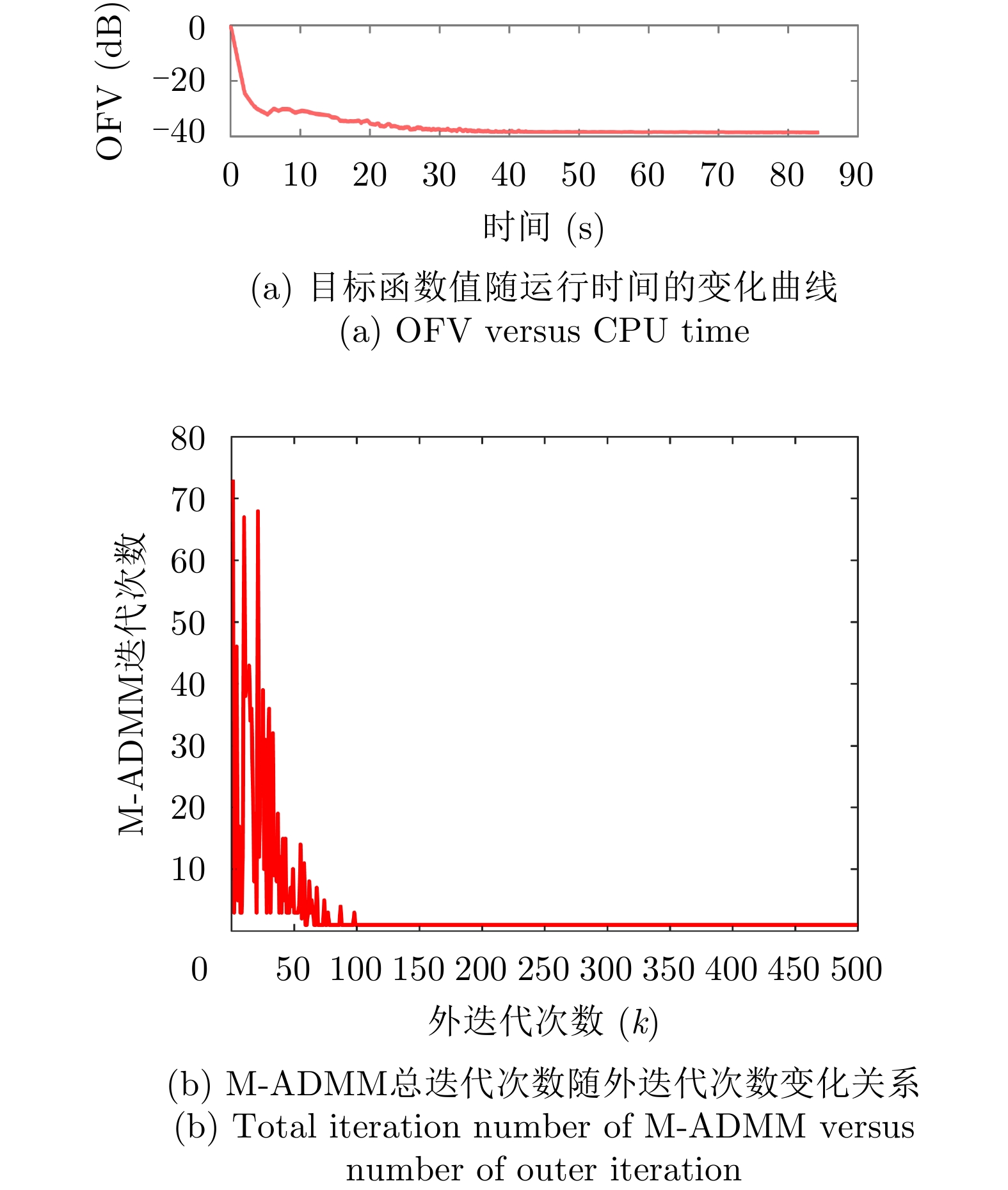
$ - 20$ dB的相同波束图凹口,即$I = 16$ ,${\boldsymbol{\varTheta }}_m^i = {75^\circ } + (i - 1){2^\circ }, i = 1,2, \cdots ,I$ ,${\boldsymbol{\varTheta }}_t^i \;\in\; [{\boldsymbol{\varTheta }}_m^i - {6^\circ },\;{\boldsymbol{\varTheta }}_m^i - {1^\circ }] \cup [{\boldsymbol{\varTheta }}_m^i + {1^\circ }, {\boldsymbol{\varTheta }}_m^i + {6^\circ }],\;\forall i$ ,${\boldsymbol{\varTheta }}_n^i \in [{40^\circ },{50^\circ }],\forall i$ ,其余设置为旁瓣${\boldsymbol{\varTheta }}_s^i,\forall i$ 。图3(a)—图3(c)分别绘制了波束图合成结果、优化问题目标函数值(OFV)随算法迭代次数的变化曲线以及最优天线位置结果;从图3(a)可以看到16个波束图具有几乎相同的波束图旁瓣水平和相同的波束图旁瓣零陷(–30 dB),达到了设计要求的比峰值旁瓣低–20 dB的零陷,且每个波束图的旁瓣水平也几乎相等,再次表明了本文min-max设计准则的有效性;从图3(b)可以看到,经过大约60次迭代后,目标函数值几乎保持不变,算法收敛;从图3(c)可以看到,与实验样例1相同,优化后天线单元的位置具有稀疏结构。
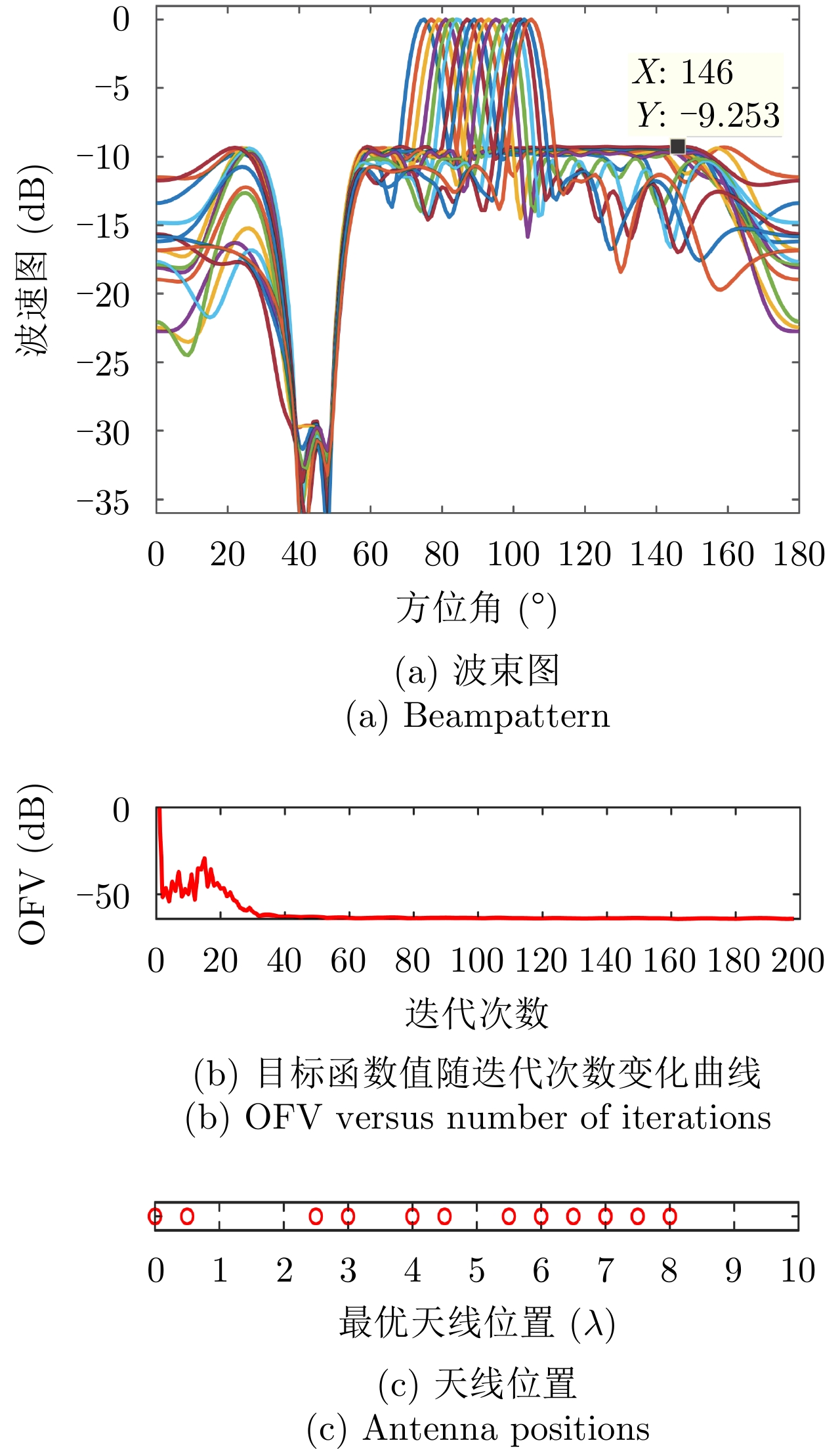
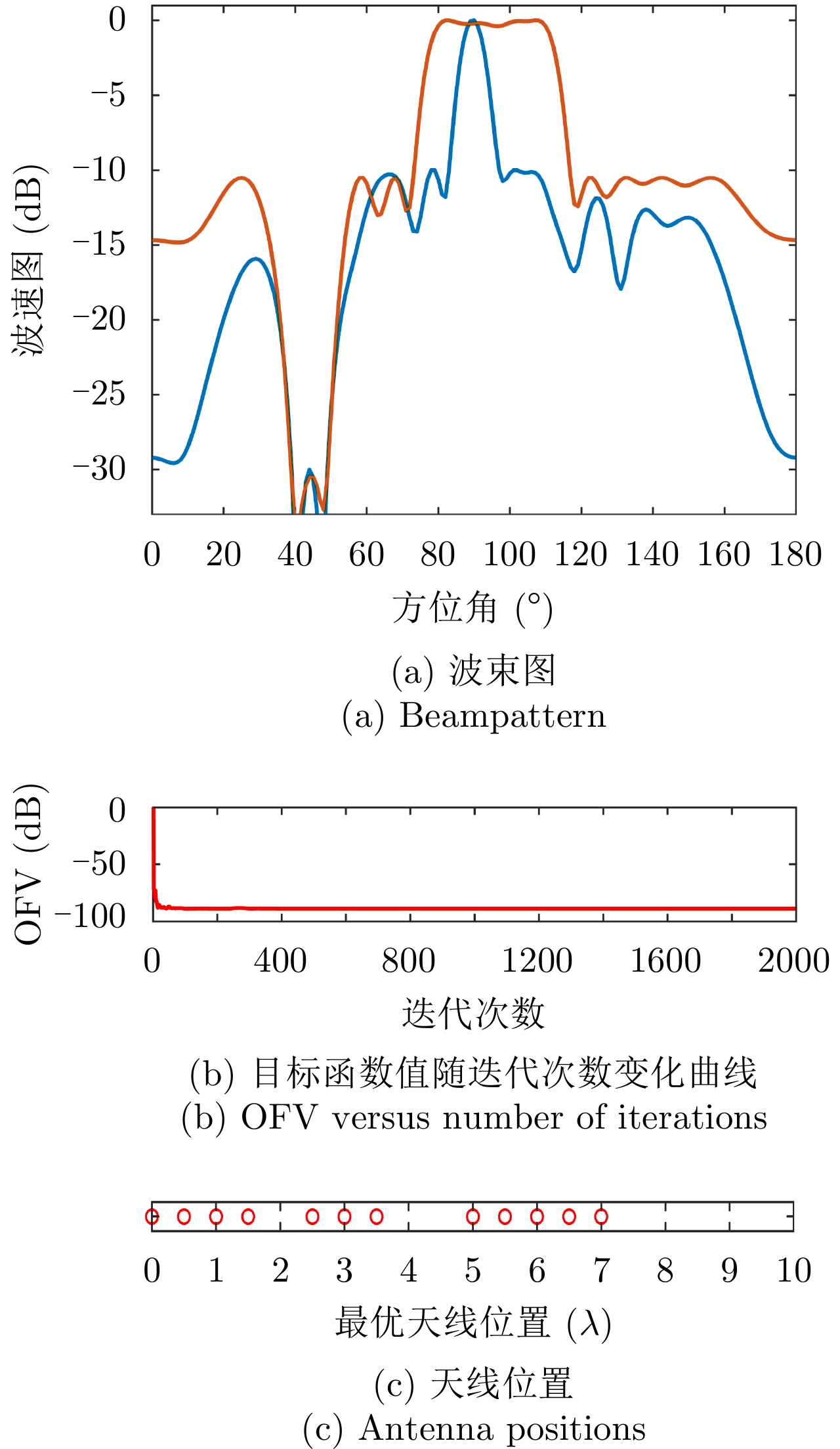
图4(a)—图4(c)给出了天线位置数
$L = 17$ ,天线数$\hat L = 12$ 时本文方法的波束图结果、优化问题目标函数值(OFV)随算法迭代次数的变化曲线以及最优天线位置结果;相比于图3(a),图4(a)波束图的峰值旁瓣增大了1 dB左右,主要因为可用天线位置减少了(稀疏孔径相同),使得波束图合成的灵活度也相应地降低了,导致了波束图旁瓣的增大。图5(a)—图5(c)给出了天线位置数
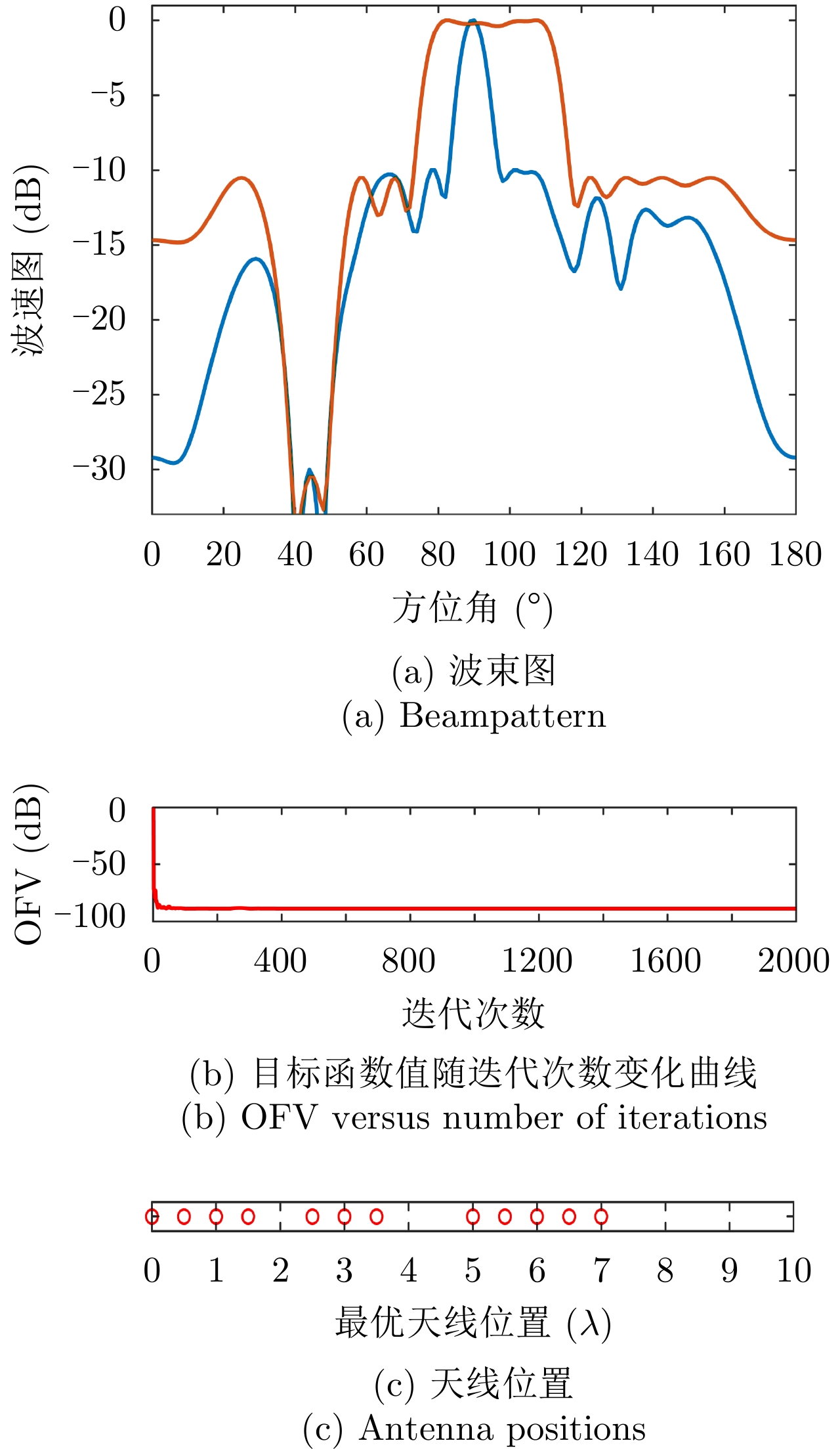
$L = 20$ ,天线数$\hat L = 15$ 时本文方法的波束图结果、优化问题目标函数值(OFV)随算法迭代次数的变化曲线以及最优天线位置结果;相比于图3(a),图5(a)波束图的峰值旁瓣降低了3 dB左右,主要因为可用天线数量增加了(稀疏孔径增大了),波束图合成的灵活度也相应的增加了,使得波束图旁瓣降低。样例 3:带两个波束图(
$I = 2$ )的集中式MIMO雷达稀疏阵列:一个宽波束,即${\boldsymbol{\varTheta }}_m^1 \in [{80^\circ }, {110^\circ }], {\boldsymbol{\varTheta }}_t^1 \in [{74^\circ },{79^\circ }] \cup [{111^\circ },{116^\circ }]$ ,一个窄波束,即${\boldsymbol{\varTheta }}_m^2 = {90^\circ },{\boldsymbol{\varTheta}} _t^2 \in [{84^\circ },{89^\circ }] \cup [{91^\circ },{96^\circ }]$ 。此外,两个波束图有比峰值旁瓣水平低$ - 20$ dB的相同波束图凹口,即${\boldsymbol{\varTheta }}_n^i \in [{40^\circ },{50^\circ }],i = 1,2$ 。其余设置为旁瓣区域${\boldsymbol{\varTheta }}_s^i,,i = 1,2$ 。图6(a)—图6(c)分别给出了仿真样例3的波束图合成结果、优化问题目标函数值(OFV)随算法迭代次数的变化曲线以及最优天线位置结果;从图6(a)可以看到2个波束图具有几乎相同的波束图峰值旁瓣水平,且具有宽波束的波束图主瓣波纹较小,也表明了本文min-max设计准则的有效性;从图6(b)可以看到,经过大约100次迭代后,目标函数值几乎保持不变,算法收敛;从图6(c)可以看到,和样例1和样例2一样,优化后天线单元的位置已经不再是等间距的,具有稀疏结构。
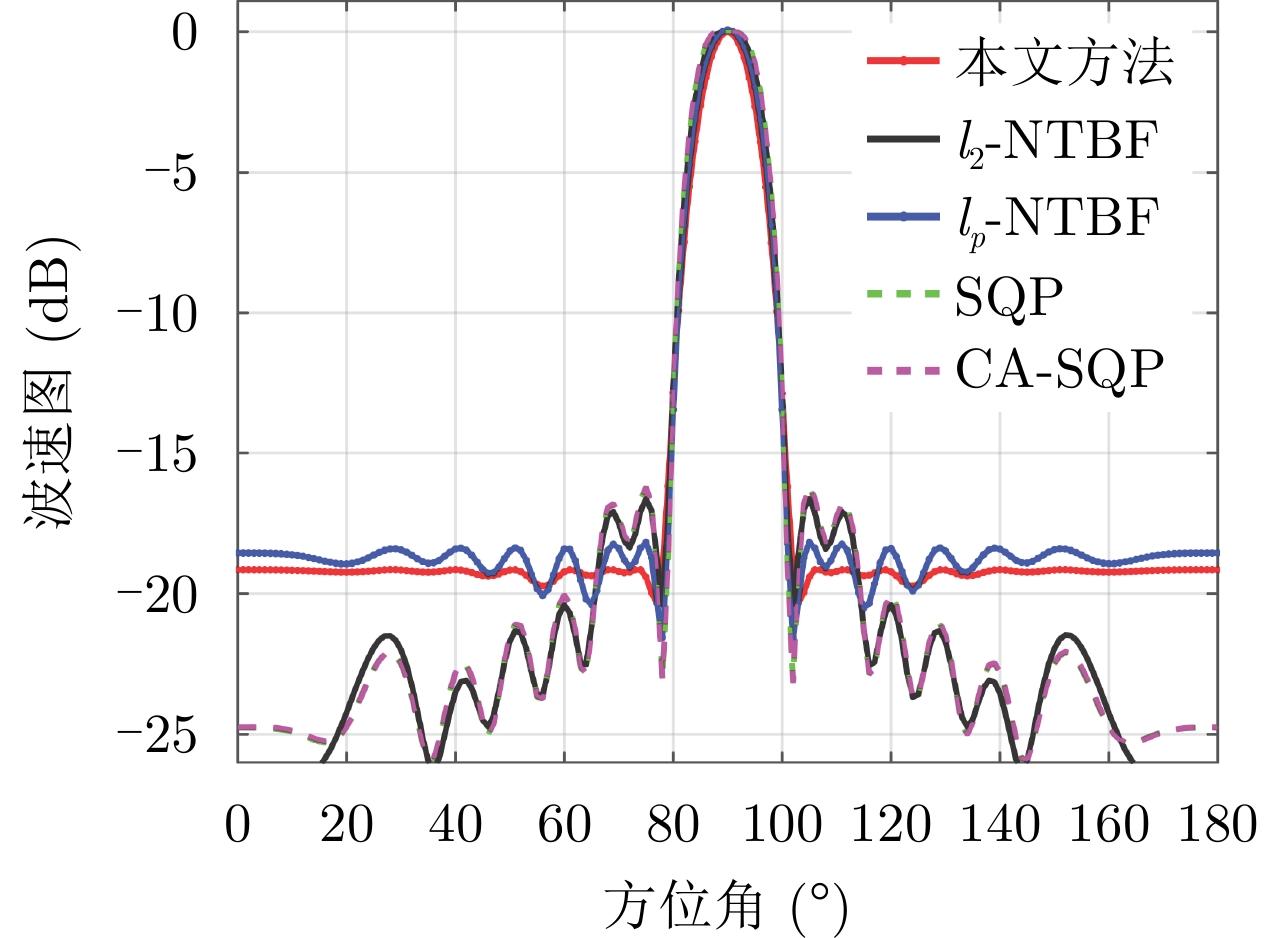
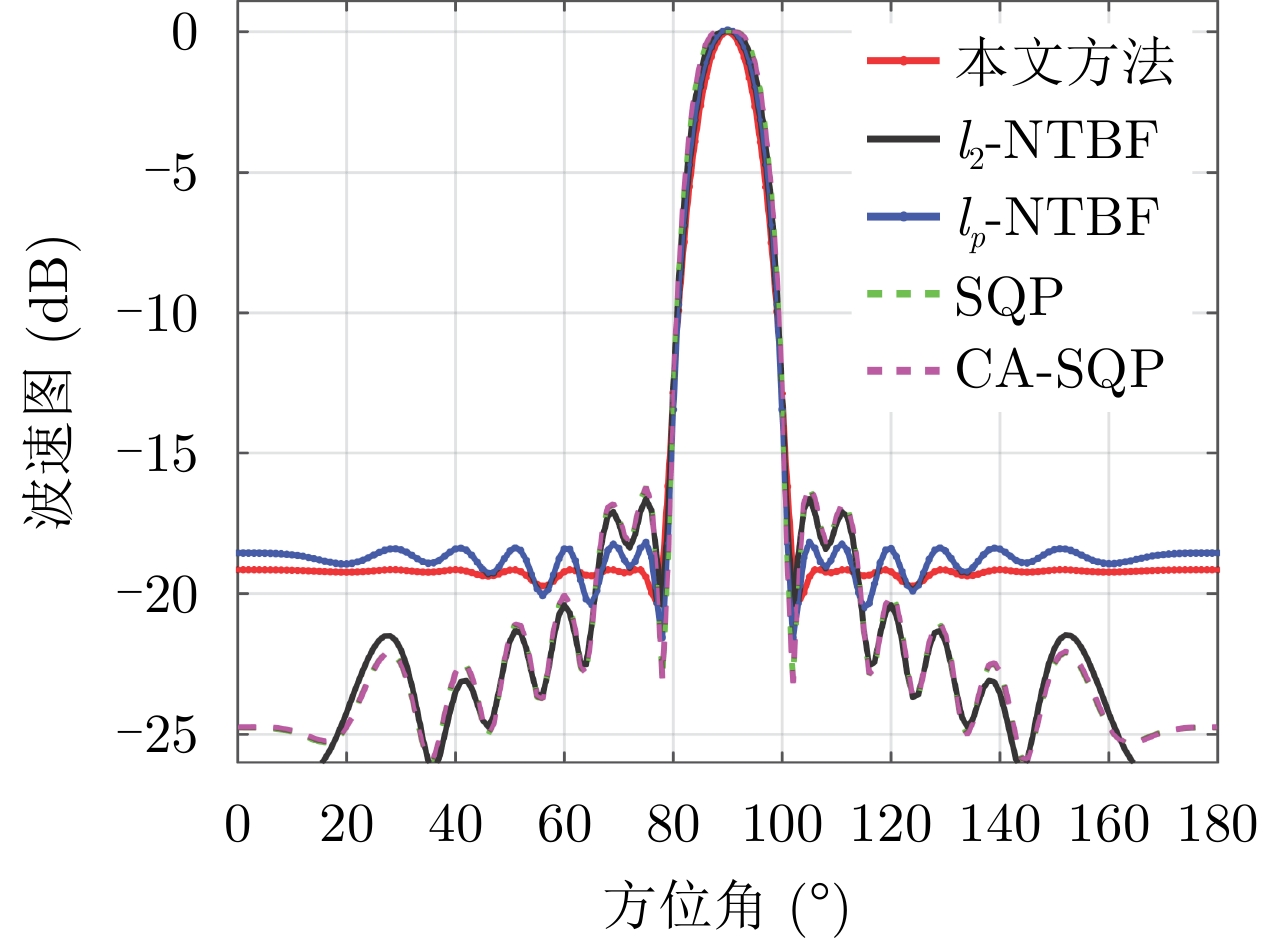
样例4:本仿真对比了现有基于
${\ell _p}$ 的波束图匹配方法 (${\ell _2} {\text{-}} {\text{NTBF}}$ 和${\ell _p} {\text{-}} {\text{NTBF}}$ )[13],基于半正定二次规划(Semi-definite Quadratic Programming, SQP)的方法[4]求解波形协方差矩阵以及根据此协方差矩阵利用循环算法获得波形(CA-SQP)的方法[18]。本文参数设置为$L = \hat L = 16$ ,间距为半波长$\bar d = {\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. } 2} = {{\rm{c}} \mathord{\left/ {\vphantom {v {2{f_c}}}} \right. } {2{f_c}}}$ ,$I = 1$ ,${\boldsymbol{\varTheta }}_m^{} = {90^\circ }$ ,${\boldsymbol{\varTheta }}_t^{} \in [{\boldsymbol{\varTheta }}_m^{} - {11^\circ }, {\boldsymbol{\varTheta }}_m^{} - {1^\circ }] \cup [{\boldsymbol{\varTheta }}_m^{} + {1^\circ },{\boldsymbol{\varTheta }}_m^{} + {11^\circ }]$ ,其余设置为旁瓣${\boldsymbol{\varTheta }}_s^{}$ 。其他参数保持不变。图7绘制了波束图对比结果,从图中可以看出本文方法所合成的波束图旁瓣最低,证明了本文方法的优越性。5. 结语
针对现有集中式MIMO雷达的发射波束图合成设计仅考虑均匀线性阵列结构无法用于非均匀布阵,以及现有稀疏结构的MIMO雷达发射波束图设计方法仅考虑在设计中合成一个发射波束图不能满足雷达多波束需求的问题,本文提出了基于min-max准则的集中式MIMO雷达多波束图合成和雷达天线阵元位置优化联合设计方法。为求解非光滑、非凸、大规模优化问题,本文结合Lawson算法、MM和ADMM推导了有效的求解算法。仿真实验表明,本文方法对MIMO雷达多波束设计和天线位置选择的有效性。该方法的提出弥补了现有集中式MIMO雷达天线位置选择方法仅合成一个波束图的不足,通过对集中式MIMO雷达的天线位置和多个波束图(多组探测波形集)同时优化,达到最优天线位置和多波束的能力,为集中式MIMO雷达向工程应用提供了有价值的参考。
-
表 1 基于波形优化和天线位置选择的MIMO雷达波束扫描算法
Table 1. Algorithm for joint waveform optimization and antenna position selection for MIMO radar beam scanning
输入参数:I, ${\boldsymbol{\varTheta }}_m^i$, ${\boldsymbol{\varTheta }}_s^i$, ${\boldsymbol{\varTheta }}_n^i$, ${\boldsymbol{\varTheta }}_t^i$, ${{\boldsymbol{W}}^i},\forall i$, ${\zeta _l},\forall l$, $\gamma $, $\hat L$, L, $\rho $, ${\delta _{{\rm{out}}} } = {10^{ - 8} }$, ${\delta _{{\rm{inner}}} } = {10^{ - 8} }$,
$\{ \{ {{\boldsymbol{X}}^i}(0),{{\boldsymbol{Z}}^i}(0),{{\boldsymbol{\varPsi }}^i}(0)\} _{i = 1}^I,{\boldsymbol{\alpha }}(0),{\boldsymbol{\bar s}}(0)\} $, $\tilde R_{m,q}^i(0) = W_{m,q}^i\left[ {{{\boldsymbol{W}}^i}; \cdots ;{{\boldsymbol{W}}^I}} \right]$, $\forall i,\forall m,\forall q$, ${K_{{\rm{max}}} }$, $k = 0$。1 WHILE {$|{\rm{obj}}(k) - {\rm{obj}}(k - 1)| > {\sigma _{{\rm{out}}} }$ & $k \le {K_{ {\rm{max} } } }$}(Lawson迭代) 2 $t = 0$;
3 WHILE $\left\{ {\dfrac{1}{I}\displaystyle\sum\limits_{i = 1}^I {\left\| { { {\boldsymbol{Z} }^i}(t) - { {\boldsymbol{Z} }^i}(t - 1)} \right\|_{\rm F}^2} > {\sigma _{{\rm{inner}}} } } \right\}$(M-ADMM迭代)4 $ \bullet $ 更新${\boldsymbol{d}}_m^i(t + 1)$; 5 $ \bullet $ 顺序更新$\{ {\boldsymbol{\bar s}}(t + 1),{\boldsymbol{\alpha }}(t + 1),\{ {{\boldsymbol{X}}^i}(t + 1)\} _{i = 1}^I\} $; 6 $ \bullet $ 更新$\{ {{\boldsymbol{Z}}^i}(t + 1)\} _{i = 1}^I$; 7 $ \bullet $ 更新$\{ {{\boldsymbol{\varPsi }}^i}(t + 1)\} _{i = 1}^I$; 8 $t: = t + 1$; 9 ENDWHILE(M-ADMM迭代结束) 10 ${{\boldsymbol{Z}}^i}(k + 1) = {{\boldsymbol{Z}}^i}(t - 1),\forall i,{\beta ^i}(k + 1) = {\bar h^i}({{\boldsymbol{Z}}^i}(k + 1)),\forall i$; 11 更新Lawson权值$w_m^i(k)$; 12 ${\rm{obj}}(k) = {\max _{m,i} }\{ G_m^i({ {\boldsymbol{Z} }^i}(k + 1),{\beta ^i}(k + 1))\}$; 13 $k: = k + 1$; 14 ENDWHILE(Lawson迭代结束) 输出:探测波形${{\boldsymbol{Z}}^i}( \star ) = {{\boldsymbol{Z}}^i}(t),i = 1,2,\cdots,I$,天线位置${\boldsymbol{\bar s}}( \star ) = {\boldsymbol{\bar s}}(t)$。 -
[1] LI Jian and STOICA P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114. doi: 10.1109/MSP.2007.904812 [2] BLUNT S D and MOKOLE E L. Overview of radar waveform diversity[J]. IEEE Aerospace and Electronic Systems Magazine, 2016, 31(11): 2–42. doi: 10.1109/MAES.2016.160071 [3] FAN Wen, LIANG Junli, and LI Jian. Constant modulus MIMO radar waveform design with minimum peak sidelobe transmit beampattern[J]. IEEE Transactions on Signal Processing, 2018, 66(16): 4207–4222. doi: 10.1109/TSP.2018.2847636 [4] STOICA P, LI Jian, and XIE Yao. On probing signal design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2007, 55(8): 4151–4161. doi: 10.1109/TSP.2007.894398 [5] ALDAYEI O, MONGA V, and RANGASWAMY M. Tractable transmit MIMO beampattern design under a constant modulus constraint[J]. IEEE Transactions on Signal Processing, 2017, 65(10): 2588–2599. doi: 10.1109/TSP.2017.2664040 [6] 黎薇萍, 陈伟超, 梁家乐. 天基TDM-MIMO雷达系统抗干扰波形设计方法[J]. 无线电工程, 2022, 52(3): 429–435. doi: 10.3969/j.issn.1003-3106.2022.03.012LI Weiping, CHEN Weichao, and LIANG Jiale. An anti-jamming waveform design method for space-based TDM-MIMO radar system[J]. Radio Engineering, 2022, 52(3): 429–435. doi: 10.3969/j.issn.1003-3106.2022.03.012 [7] 杨力萍, 廖可非, 欧阳缮. 分布式MIMO雷达时间与阵面资源自适应调度算法[J]. 无线电工程, 2022, 52(7): 1136–1144. doi: 10.3969/j.issn.1003-3106.2022.07.005YANG Liping, LIAO Kefei, and OUYANG Shan. Adaptive scheduling algorithm for time and array resources of distributed MIMO radar[J]. Radio Engineering, 2022, 52(7): 1136–1144. doi: 10.3969/j.issn.1003-3106.2022.07.005 [8] LIU Yanhui, LIU Qinghuo, and NIE Zaiping. Reducing the number of elements in multiple-pattern linear arrays by the extended matrix pencil methods[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(2): 652–660. doi: 10.1109/TAP.2013.2292529 [9] VESCOVO R. Reconfigurability and beam scanning with phase-only control for antenna arrays[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(6): 1555–1565. doi: 10.1109/TAP.2008.923297 [10] ZHANG Xuan, LIANG Junli, FAN Xuhui, et al. Reconfigurable array beampattern synthesis via conceptual sensor network modeling and computation[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(6): 4512–4525. doi: 10.1109/TAP.2020.2972401 [11] FUHRMANN D R and ANTONIO G S. Transmit beamforming for MIMO radar systems using signal cross-correlation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 171–186. doi: 10.1109/TAES.2008.4516997 [12] HE Hao, STOICA P, and LI Jian. Wideband MIMO systems: Signal design for transmit beampattern synthesis[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 618–628. doi: 10.1109/TSP.2010.2091410 [13] FAN Wen, LIANG Junli, YU Guoyang, et al. MIMO radar waveform design for quasi-equiripple transmit beampattern synthesis via weighted l p-minimization[J]. IEEE Transactions on Signal Processing, 2019, 67(13): 3397–3411. doi: 10.1109/TSP.2019.2917871 [14] ROBERTS W, XU Luzhou, LI Jian, et al. Sparse antenna array design for MIMO active sensing applications[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(3): 846–858. doi: 10.1109/TAP.2010.2103550 [15] CHENG Ziyang, LU Yanxi, HE Zishu, et al. Joint optimization of covariance matrix and antenna position for MIMO radar transmit beampattern matching design[C]. 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, USA, 2018: 1073–1077. [16] 崔国龙, 余显祥, 杨婧, 等. 认知雷达波形优化设计方法综述[J]. 雷达学报, 2019, 8(5): 537–557. doi: 10.12000/JR19072CUI Guolong, YU Xianxiang, YANG Jing, et al. An overview of waveform optimization methods for cognitive radar[J]. Journal of Radars, 2019, 8(5): 537–557. doi: 10.12000/JR19072 [17] LIPOR J, AHMED S, and ALOUINI M S. Fourier-based transmit beampattern design using MIMO radar[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2226–2235. doi: 10.1109/TSP.2014.2307838 [18] STOICA P, LI Jian, and ZHU Xumin. Waveform synthesis for diversity-based transmit beampattern design[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2593–2598. doi: 10.1109/TSP.2007.916139 [19] AHMED S and ALOUINI M. A survey of correlated waveform design for multifunction software radar[J]. IEEE Aerospace and Electronic Systems Magazine, 2016, 31(3): 19–31. doi: 10.1109/MAES.2016.150051 [20] HUA G and ABEYSEKERA S S. MIMO radar transmit beampattern design with ripple and transition band control[J]. IEEE Transactions on Signal Processing, 2013, 61(11): 2963–2974. doi: 10.1109/TSP.2013.2252173 [21] 何子述, 韩春林, 刘波. MIMO雷达概念及其技术特点分析[J]. 电子学报, 2005, 33(12A): 2441–2445.HE Zishu, HAN Chunlin, and LIU Bo. MIMO radar and its technical characteristic analyses[J]. Acta Electronica Sinica, 2005, 33(12A): 2441–2445. [22] IMANI S, NAYEBI M M, and ALI GHORASHI S. Transmit signal design in colocated MIMO radar without covariance matrix optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(5): 2178–2186. doi: 10.1109/TAES.2017.2686618 [23] CHENG Ziyang, HE Zishu, ZHANG Shengmiao, et al. Constant modulus waveform design for MIMO radar transmit beampattern[J]. IEEE Transactions on Signal Processing, 2017, 65(18): 4912–4923. doi: 10.1109/TSP.2017.2718976 [24] YU Xianxiang, CUI Guolong, YANG Jing, et al. Wideband MIMO radar waveform design[J]. IEEE Transactions on Signal Processing, 2019, 67(13): 3487–3501. doi: 10.1109/TSP.2019.2916732 [25] CHENG Ziyang, HAN Chunlin, LIAO Bin, et al. Communication-aware waveform design for MIMO radar with good transmit beampattern[J]. IEEE Transactions on Signal Processing, 2018, 66(21): 5549–5562. doi: 10.1109/TSP.2018.2868042 [26] ALHUJAILI K, MONGA V, and RANGASWAMY M. Transmit MIMO radar beampattern design via optimization on the complex circle manifold[J]. IEEE Transactions on Signal Processing, 2019, 67(13): 3561–3575. doi: 10.1109/TSP.2019.2914884 [27] 王璐璐, 王宏强, 王满喜, 等. 雷达目标检测的最优波形设计综述[J]. 雷达学报, 2016, 5(5): 487–498. doi: 10.12000/JR16084WANG Lulu, WANG Hongqiang, WANG Manxi, et al. An overview of radar waveform optimization for target detection[J]. Journal of Radars, 2016, 5(5): 487–498. doi: 10.12000/JR16084 [28] 何子述, 李军, 刘红明, 等. MIMO雷达[M]. 北京: 国防工业出版社, 2017.HE Zishu, LI Jun, LIU Hongming, et al. MIMO Radar[M]. Beijing: National Defense Industry Press, 2017. [29] DENG Minglong, CHENG Ziyang, and HE Zishu. Co-Design of Waveform correlation matrix and antenna positions for MIMO radar transmit beampattern formation[J]. IEEE Sensors Journal, 2020, 20(13): 7326–7336. doi: 10.1109/JSEN.2020.2977686 [30] ROCCA P, OLIVERI G, MAILLOUX R J, et al. Unconventional phased array architectures and design methodologies—A review[J]. Proceedings of the IEEE, 2016, 104(3): 544–560. doi: 10.1109/JPROC.2015.2512389 [31] LIU Yanhui, CHENG Juan, XU Kaida, et al. Reducing the number of elements in the synthesis of a broadband linear array with multiple simultaneous frequency-invariant beam patterns[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(11): 5838–5848. doi: 10.1109/TAP.2018.2862361 [32] SHEN Haiou and WANG Buhong. An effective method for synthesizing multiple-pattern linear arrays with a reduced number of antenna elements[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(5): 2358–2366. doi: 10.1109/TAP.2017.2679344 [33] HE Hao, LI Jian, and STOICA P. Waveform Design for Active Sensing Systems: A Computational Approach[M]. Cambridge: Cambridge University Press, 2012. [34] CUI Guolong, YU Xianxiang, YANG Ya, et al. Cognitive phase-only sequence design with desired correlation and stopband properties[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2924–2935. doi: 10.1109/TAES.2017.2721238 [35] FAN Wen, LIANG Junli, CHEN Zihao, et al. Spectrally compatible aperiodic sequence set design with low cross and auto-correlation PSL[J]. Signal Processing, 2021, 183: 107960. doi: 10.1016/j.sigpro.2020.107960 [36] FAN Wen, LIANG Junli, YU Guoyang, et al. Minimum local peak sidelobe level waveform design with correlation and/or spectral constraints[J]. Signal Processing, 2020, 171: 107450. doi: 10.1016/j.sigpro.2019.107450 [37] FAN Wen, LIANG Junli, SO H C, et al. Min-max metric for spectrally compatible waveform design via log-exponential smoothing[J]. IEEE Transactions on Signal Processing, 2020, 68: 1075–1090. doi: 10.1109/TSP.2020.2969043 [38] AUBRY A, MAIO A D, and HUANG Yongwei. MIMO radar beampattern design via PSL/ISL optimization[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3955–3967. doi: 10.1109/TSP.2016.2543207 [39] TSENG C Y and GRIFFITHS L J. A simple algorithm to achieve desired patterns for arbitrary arrays[J]. IEEE Transactions on Signal Processing, 1992, 40(11): 2737–2746. doi: 10.1109/78.165660 [40] LORENZ R G and BOYD S P. Robust minimum variance beamforming[J]. IEEE Transactions on Signal Processing, 2005, 53(5): 1684–1696. doi: 10.1109/TSP.2005.845436 [41] NAI S E, SER W, YU Zhuliang, et al. Beampattern synthesis for linear and planar arrays with antenna selection by convex optimization[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(12): 3923–3930. doi: 10.1109/TAP.2010.2078446 [42] LAWSON C. Contributions to the theory of linear least maximum approximation[D]. [Ph. D. dissertation], University of California, 1961. [43] RICE J and USOW K. The Lawson algorithm and extensions[J]. Mathematics of Computation, 1968, 22(101): 118–127. doi: 10.1090/S0025-5718-1968-0232137-4 [44] ELLACITT S and WILLIAMS J. Linear Chebyshev approximation in the complex plane using Lawson’s algorithm[J]. Mathematics of Computation, 1976, 30(133): 35–44. doi: 10.2307/2005427 [45] WANG Yu, YIN Wotao, and ZENG Jinshan. Global convergence of ADMM in nonconvex nonsmooth optimization[J]. Journal of Scientific Computing, 2019, 78(1): 29–63. doi: 10.1007/s10915-018-0757-z [46] HONG Mingyi, LUO Zhiquan, and RAZAVIYAYN M. Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems[J]. SIAM Journal on Optimization, 2016, 26(1): 337–364. doi: 10.1137/140990309 [47] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2011, 3(1): 1–122. doi: 10.1561/2200000016 [48] FAN Wen, LIANG Junli, FAN Xuhui, et al. A unified sparse array design framework for beampattern Synthesis[J]. Signal Processing, 2021, 182: 107930. doi: 10.1016/j.sigpro.2020.107930 [49] SUN Ying, BABU P, and PALOMAR D P. Majorization-minimization algorithms in signal processing, communications, and machine learning[J]. IEEE Transactions on Signal Processing, 2017, 65(3): 794–816. doi: 10.1109/TSP.2016.2601299 [50] RAZAVIYAYN M, HONG Mingyi, and LUO Zhiquan. A unified convergence analysis of block successive minimization methods for nonsmooth optimization[J]. SIAM Journal on Optimization, 2013, 23(2): 1126–1153. doi: 10.1137/120891009 [51] HONG Mingyi, RAZAVIYAYN M, LUO Zhiquan, et al. A unified algorithmic framework for block-structured optimization involving big data: With applications in machine learning and signal processing[J]. IEEE Signal Processing Magazine, 2016, 33(1): 57–77. doi: 10.1109/MSP.2015.2481563 [52] FAN Wen, LIANG Junli, LU Guangshan, et al. Spectrally-agile waveform design for wideband MIMO radar transmit beampattern synthesis via majorization-ADMM[J]. IEEE Transactions on Signal Processing, 2021, 69: 1563–1578. doi: 10.1109/TSP.2021.3052997 [53] TROPP J A, DHILLON I S, HEATH R W, et al. Designing structured tight frames via an alternating projection method[J]. IEEE Transactions on Information Theory, 2005, 51(1): 188–209. doi: 10.1109/TIT.2004.839492 期刊类型引用(3)
1. 胡雪瑶,梁灿,卢珊珊,王在洋,郑乐,李阳. 基于矩阵填充的随机步进频雷达高分辨距离-多普勒谱稀疏恢复方法. 雷达学报. 2024(01): 200-214 .  本站查看
本站查看2. 李正杰,谢军伟,张浩为,温泉,刘斌. 一种低截获背景下的集中式MIMO雷达快速功率分配算法. 雷达学报. 2023(03): 602-615 .  本站查看
本站查看3. 范文,李淳泽,赵勇,张航. 复杂环境下雷达抗干扰及多功能一体化波形设计方法研究. 无线电通信技术. 2023(05): 960-970 .  百度学术
百度学术其他类型引用(3)
-



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公

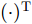
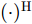
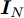
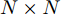
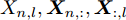
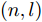
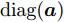
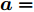
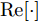
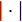
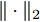
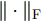
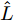
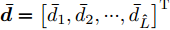
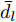
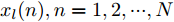
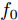
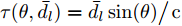

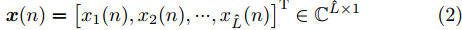
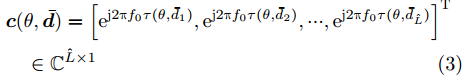
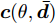
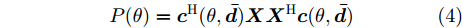
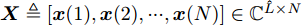
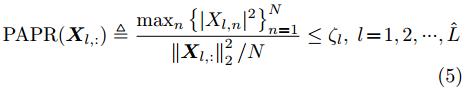
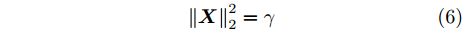
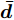
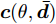
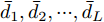
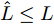
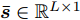
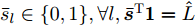
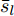
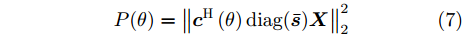
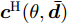
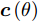
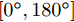
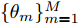
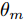
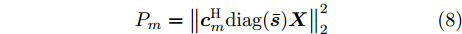
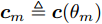
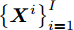
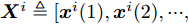
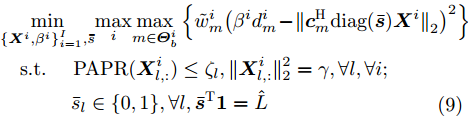
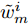
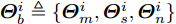
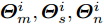
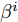
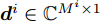
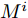
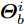
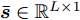
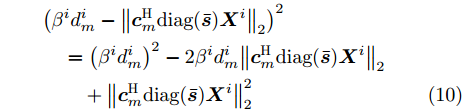
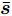
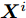
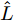
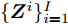
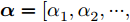
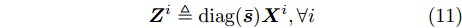
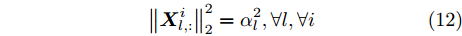
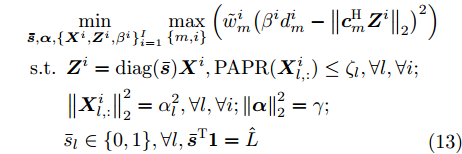
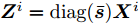
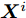
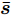
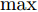
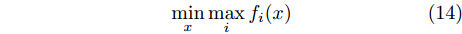
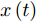
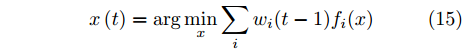
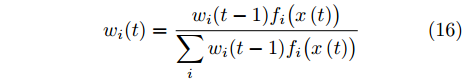
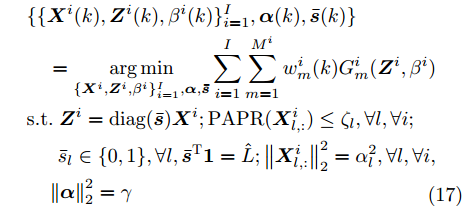
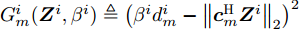
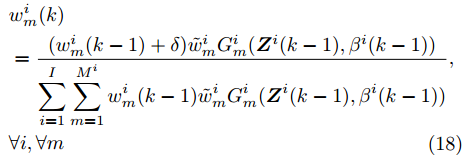
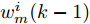
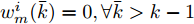
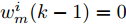
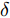
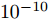
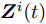
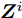
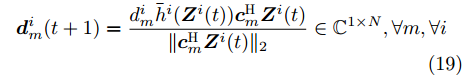
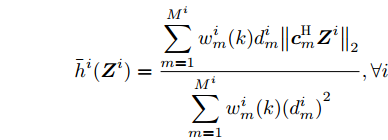
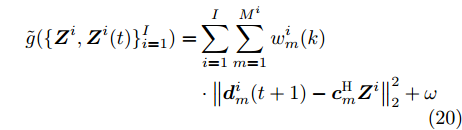
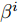
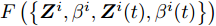
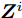
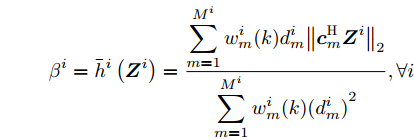
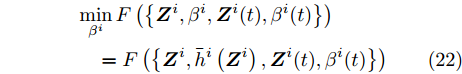
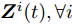
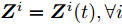
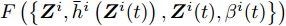
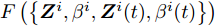
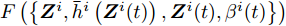

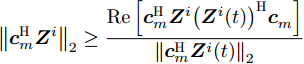
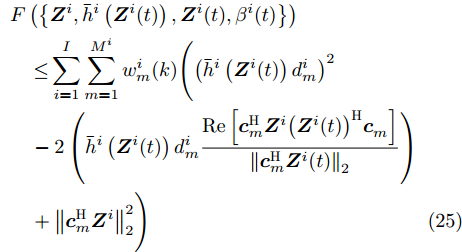
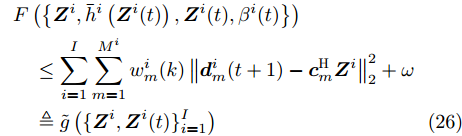
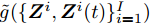
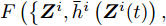
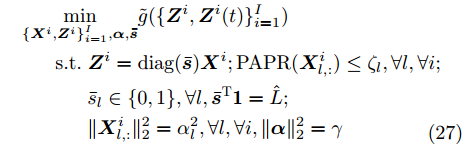
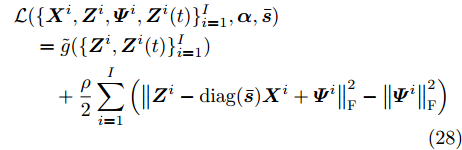
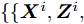
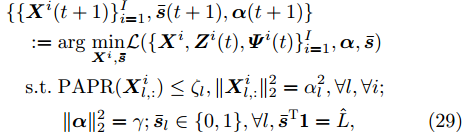
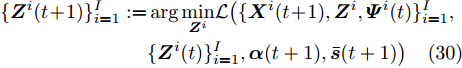
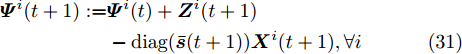
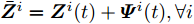
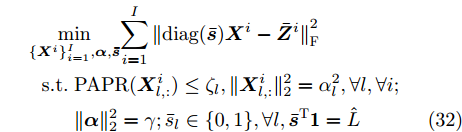
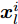
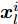
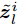
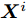
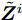
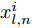
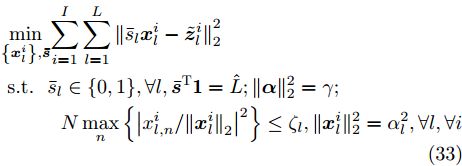
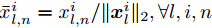
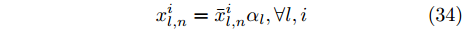
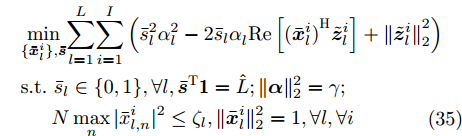
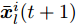
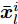
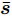
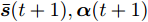
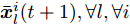
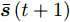
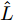
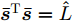
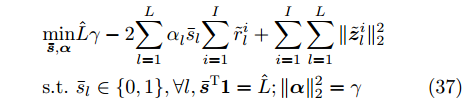
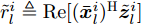
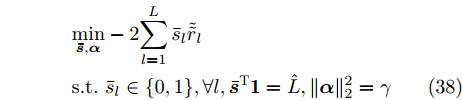
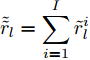
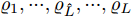
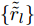
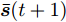
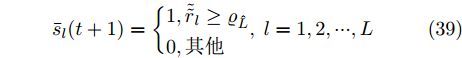
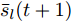
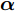
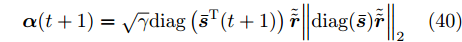
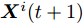
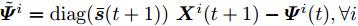
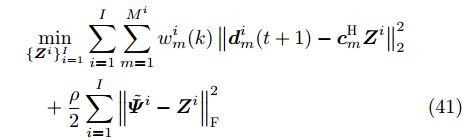
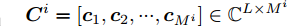
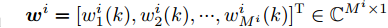
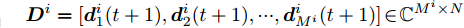
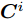
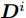
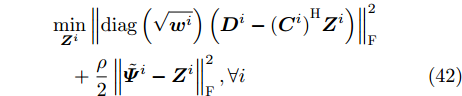
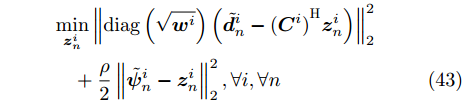
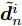
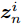
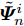
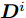
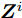
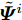
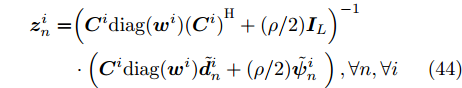
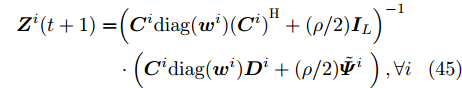
 下载:
下载:
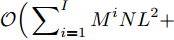
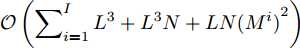
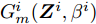
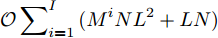
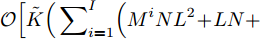
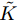
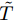
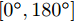
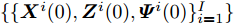
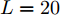
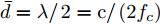
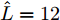
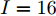


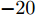
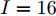
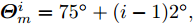
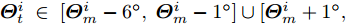










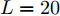
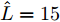


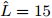

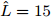

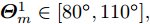
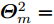
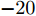
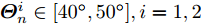
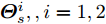

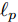
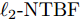
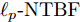
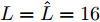
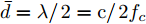

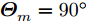
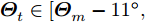
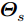

 下载:
下载:












 百度学术
百度学术