基于Transformer网络的机载雷达多目标跟踪方法

李文娜; 张顺生; 王文钦

doi:10.12000/JR22009

基于Transformer网络的机载雷达多目标跟踪方法

DOI: 10.12000/JR22009

1.
电子科技大学电子科学技术研究院成都 611731
2.
电子科技大学信息与通信工程学院成都 611731

基金项目: 国家自然科学基金(62171092)

详细信息

作者简介:
李文娜(1997–)，女，现为电子科技大学在读硕士研究生，主要研究方向为雷达目标跟踪

张顺生(1980–)，男，研究员，博士生导师，主要研究方向为雷达信号处理

王文钦(1979–)，男，教授，博士生导师，主要研究方向为阵列处理及其在雷达、通信和电子对抗中的应用

通讯作者:
张顺生 zhangss@uestc.edu.cn

责任主编：胡程 Corresponding Editor: HU Cheng
中图分类号: TN953
计量
- 文章访问数: 2722
- HTML全文浏览量: 947
- PDF下载量: 399
- 被引次数: 0
出版历程
- 收稿日期: 2022-01-10
- 修回日期: 2022-03-03
- 网络出版日期: 2022-03-21
- 刊出日期: 2022-06-28

Multitarget-tracking Method for Airborne Radar Based on a Transformer Network

1.
Research Institute of Electronic Science and Technology, University of Science and Technology of China, Chengdu 611731, China
2.
School of Information and Communication Engineering, University of Science and Technology of China, Chengdu 611731, China

Funds: The National Natural Science Foundation of China (62171092)

More Information

Corresponding author: ZHANG Shunsheng, zhangss@uestc.edu.cn

摘要

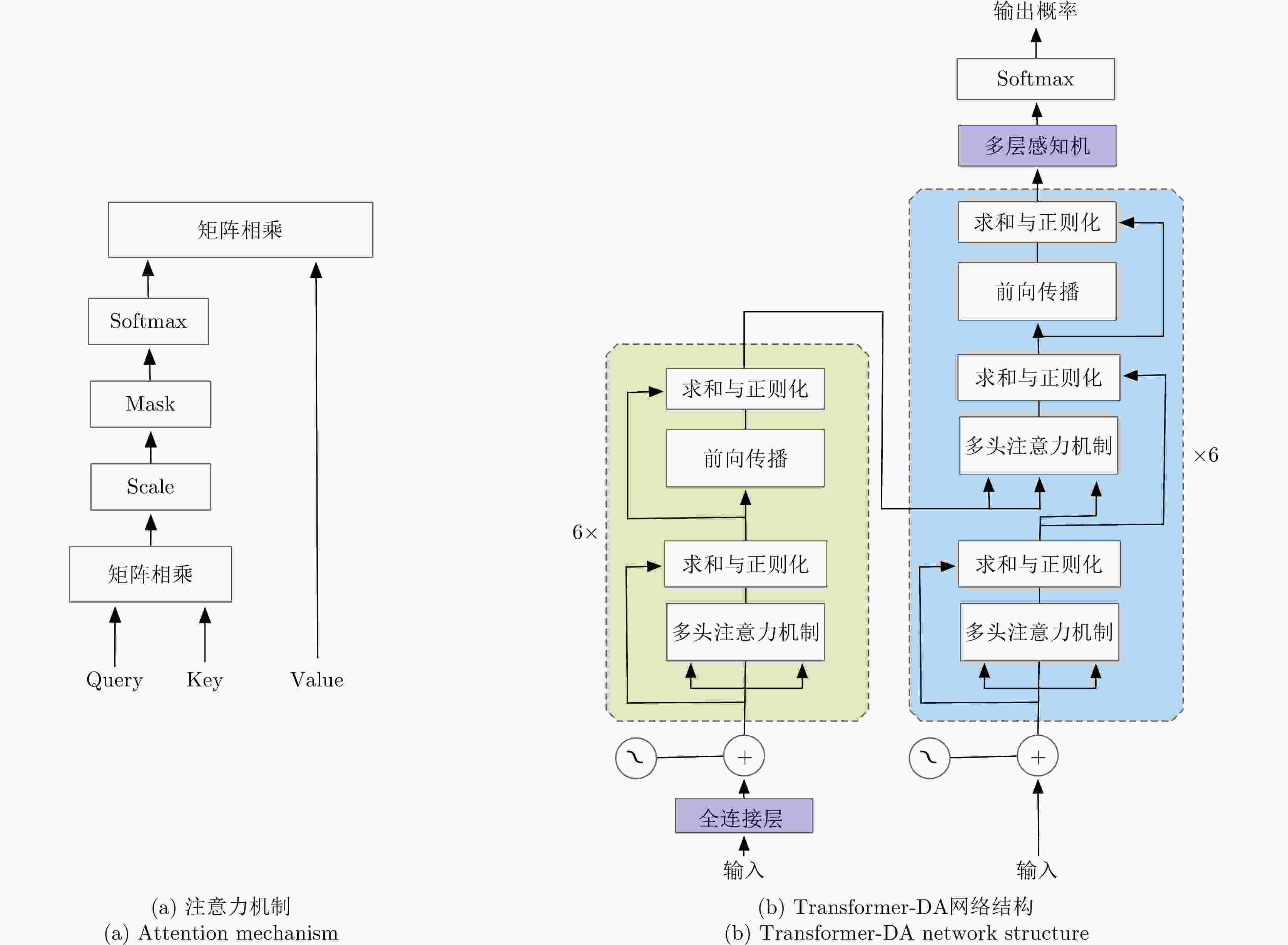
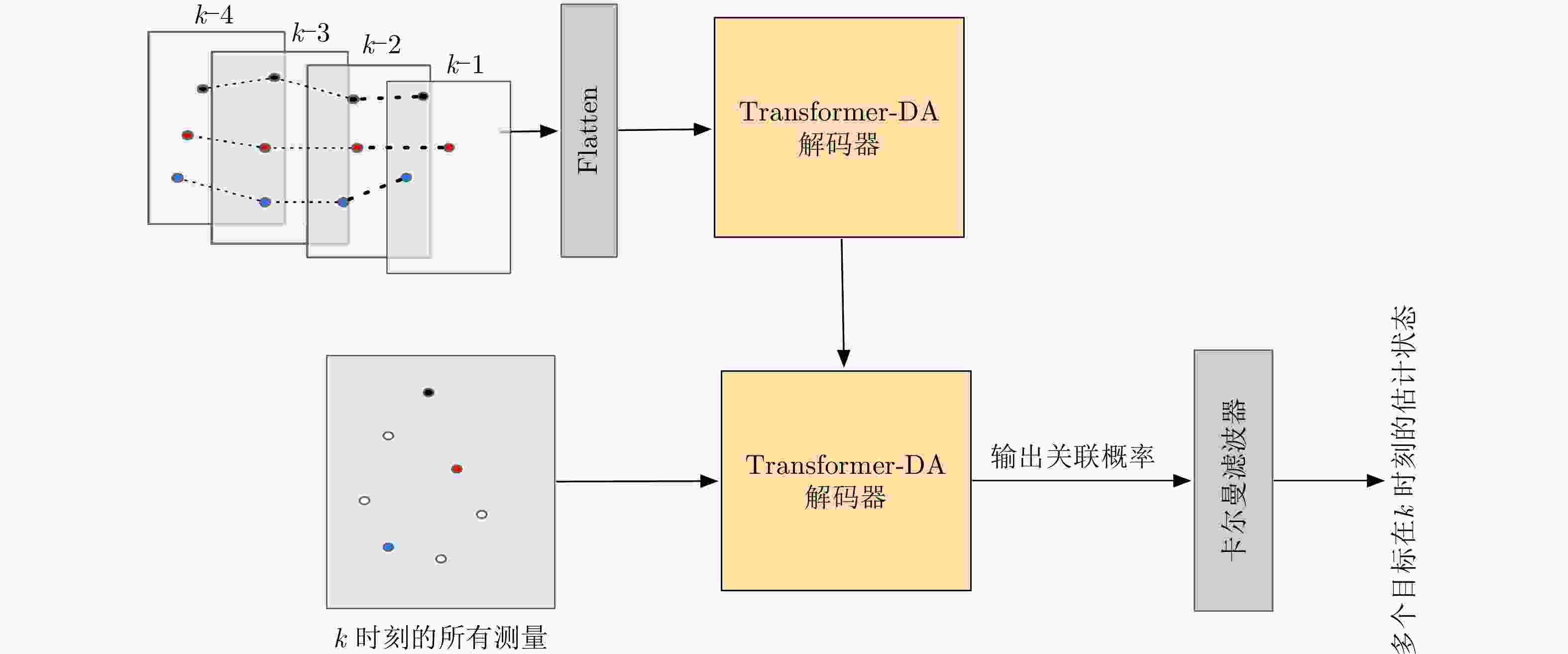
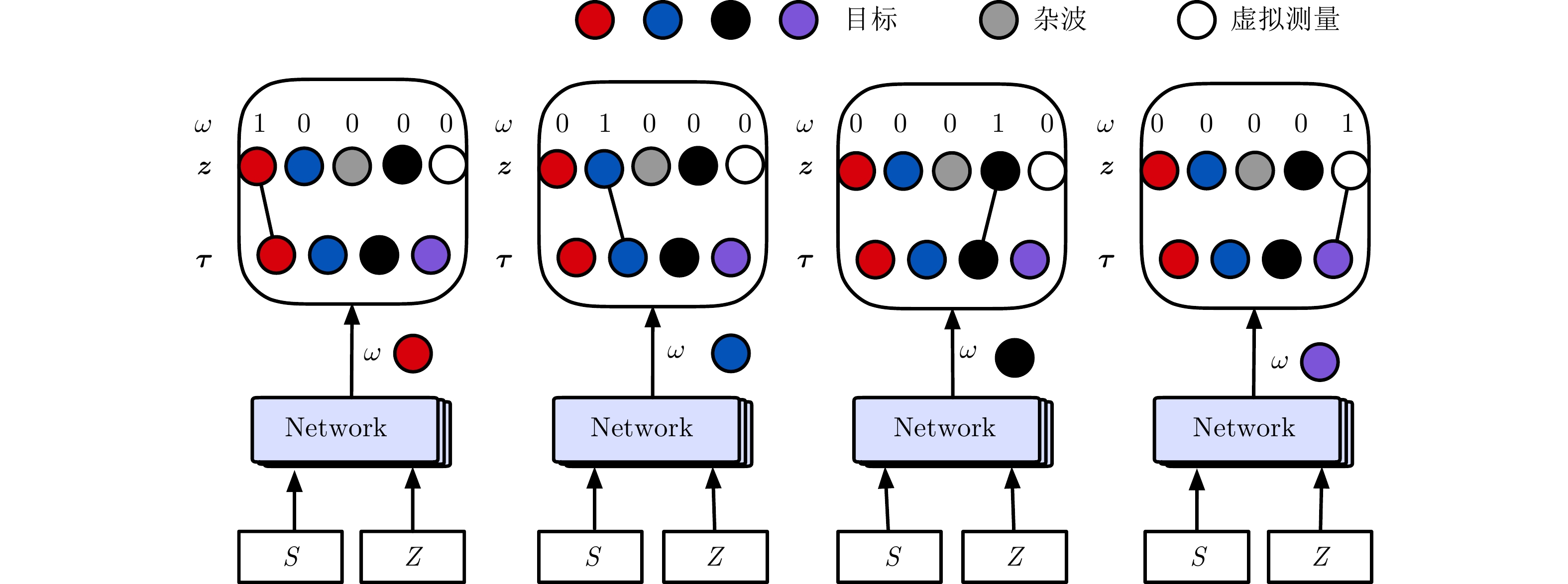
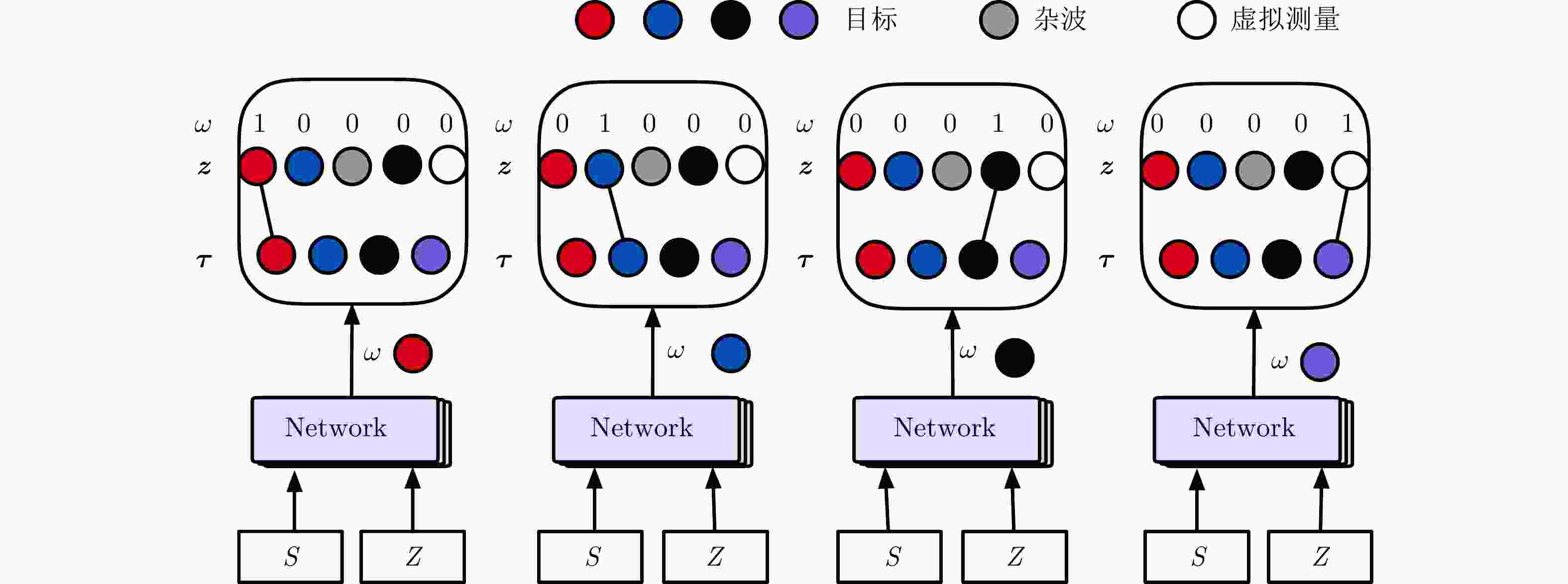
摘要: 传统的多目标跟踪数据关联算法需要提前知晓目标运动模型和杂波密度等先验信息，然而这些先验信息在跟踪之前无法及时准确地获取。针对这个问题，提出一种基于Transformer网络的多目标跟踪数据关联算法。首先，考虑到传感器会存在漏检的情况，引入虚拟量测来重新建立数据关联模型。在此基础上，提出基于Transformer网络的数据关联方法来解决多目标与多量测的匹配问题。同时，设计了一种掩蔽交叉熵损失与重叠度损失相结合的损失函数(MCD)用于优化网络参数。仿真和实测数据结果表明：在不同检测概率条件下，所提算法性能均优于经典的数据关联算法和基于双向长短时记忆网络的算法。
- 机载雷达 /
- 多目标跟踪 /
- 数据关联 /
- Transformer网络 /
- 注意力机制
Abstract: Conventional multitarget-tracking data association algorithms must have prior information, such as the target motion model and clutter density. However, such prior information cannot be obtained timely and accurately before tracking. To address this issue, a data association algorithm for multitarget tracking based on a transformer network is proposed. First, considering that the radar may not perform accurate detected the target, virtual measurements are performed to re-establish the data association model. Thus, a data association method based on the transformer network is proposed to solve the matching problem of multitargets and multimeasurements. Moreover, a loss function combining Masked Cross entropy loss and Dice (MCD) loss is designed to optimize the network parameters. Simulation data and real measurement data results show that the proposed algorithm outperforms classic data association algorithms and algorithms based on bidirectional long short-term memory network under varying detection probability conditions.
- Airborne radar /
- Multitarget-tracking /
- Data association /
- Transformer network /
- Attention mechanism

HTML全文

图 1 每个目标与所有量测的匹配关系示意图

Figure 1. A diagram of the matching relationship between each target and all measurements

下载: 全尺寸图片幻灯片

图 2 注意力机制与Transformer-DA网络结构

Figure 2. Attention mechanism and Transformer-DA network structure

下载: 全尺寸图片幻灯片

图 3 基于Transformer-DA的多目标跟踪框架

Figure 3. Multitarget-tracking framework based on Transformer-DA

下载: 全尺寸图片幻灯片

图 4 ${E_\lambda } = 80$, ${p_d} = 0.99$时的仿真轨迹与量测

Figure 4. Simulation trajectory and measurement when ${E_\lambda } = 80$, ${p_d} = 0.99$

下载: 全尺寸图片幻灯片

图 5 ${E_\lambda } = 80$, ${p_d} = 0.99$时不同算法的跟踪结果(使用仿真数据)

Figure 5. Tracking results of different algorithms when ${E_\lambda } = 80$, ${p_d} = 0.99$ (using simulation data)

下载: 全尺寸图片幻灯片

图 6 ${E_\lambda } = 80$, ${p_d} = 0.99$下不同算法的OSPA距离(使用仿真数据)

Figure 6. OSPA distance of different algorithms when ${E_\lambda } = 80$, ${p_d} = 0.99$ (using simulation data)

下载: 全尺寸图片幻灯片

图 7 ${E_\lambda } = 80$, ${p_d} = 0.99$时的真实轨迹与仿真量测

Figure 7. Real trajectory and simulation measurements when ${E_\lambda } = 80$, ${p_d} = 0.99$

下载: 全尺寸图片幻灯片

图 8 ${E_\lambda } = 80$, ${p_d} = 0.99$时不同算法的跟踪结果(使用实际数据)

Figure 8. Tracking results of different algorithms when ${E_\lambda } = 80$, ${p_d} = 0.99$ (using actual data)

下载: 全尺寸图片幻灯片

图 9 ${E_\lambda } = 80$, ${p_d} = 0.99$时不同算法的OSPA距离(使用实际数据)

Figure 9. OSPA distance of different algorithms when ${E_\lambda } = 80$, ${p_d} = 0.99$ (using actual data)

下载: 全尺寸图片幻灯片

表 1 Transformer-DA网络参数

Table 1. Transformer-DA network parameters

参数	数值
编码器输入数据维度	5$ \times $20
解码器输入数据维度	100$ \times $4
输出数据维度	100$ \times $6
多头注意力的头数	8
编码器输入最大序列长度	5
解码器输入最大序列长度	100
解码器数目	6
编码器数目	6
前向传播网络大小	512
隐藏层大小	512
Dropout率	0.1

下载: 导出CSV

表 2 使用仿真数据时算法在不同检测概率下的OSPA对比

Table 2. OSPA comparison of the algorithm under different detection probabilities when using simulation data

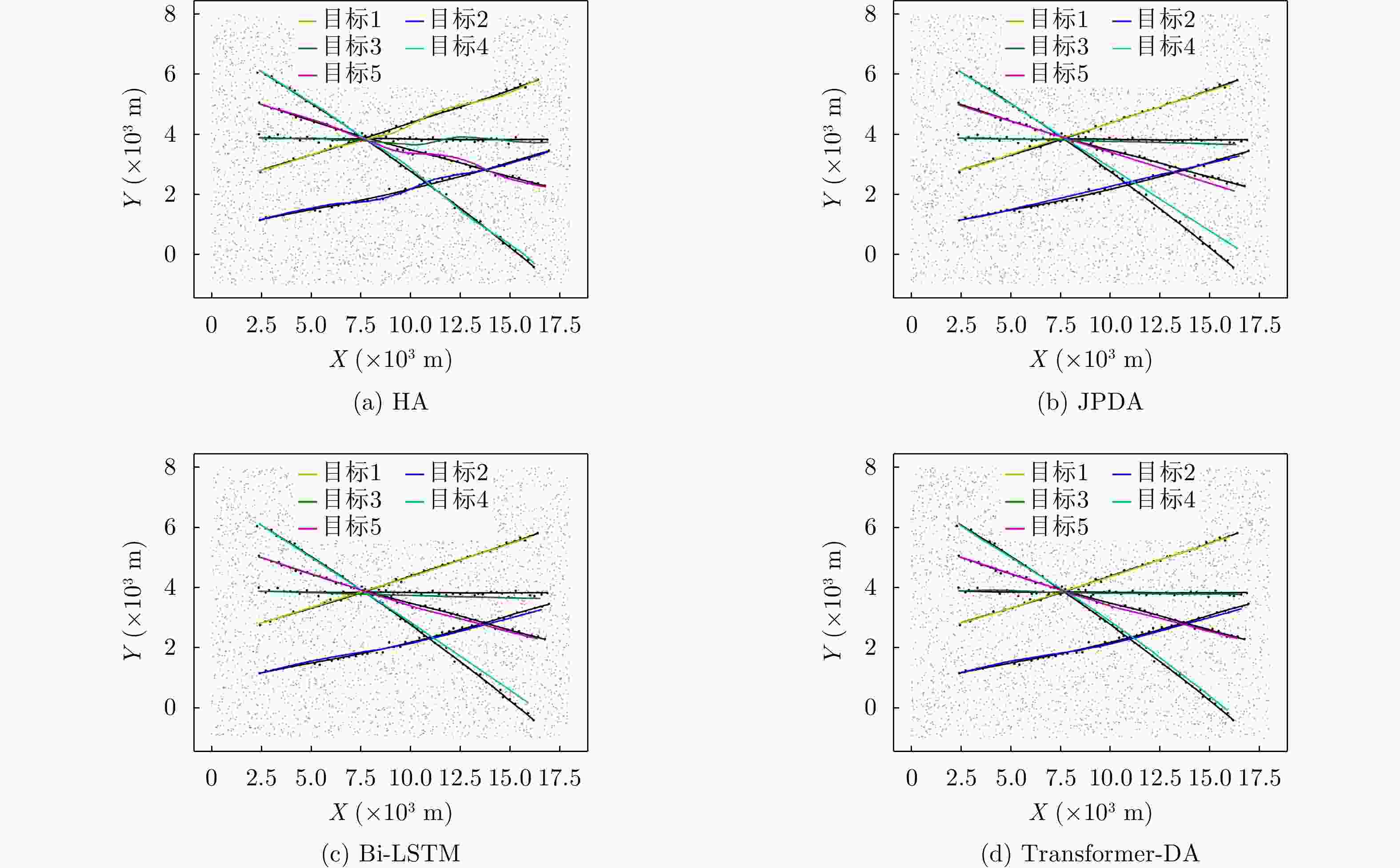
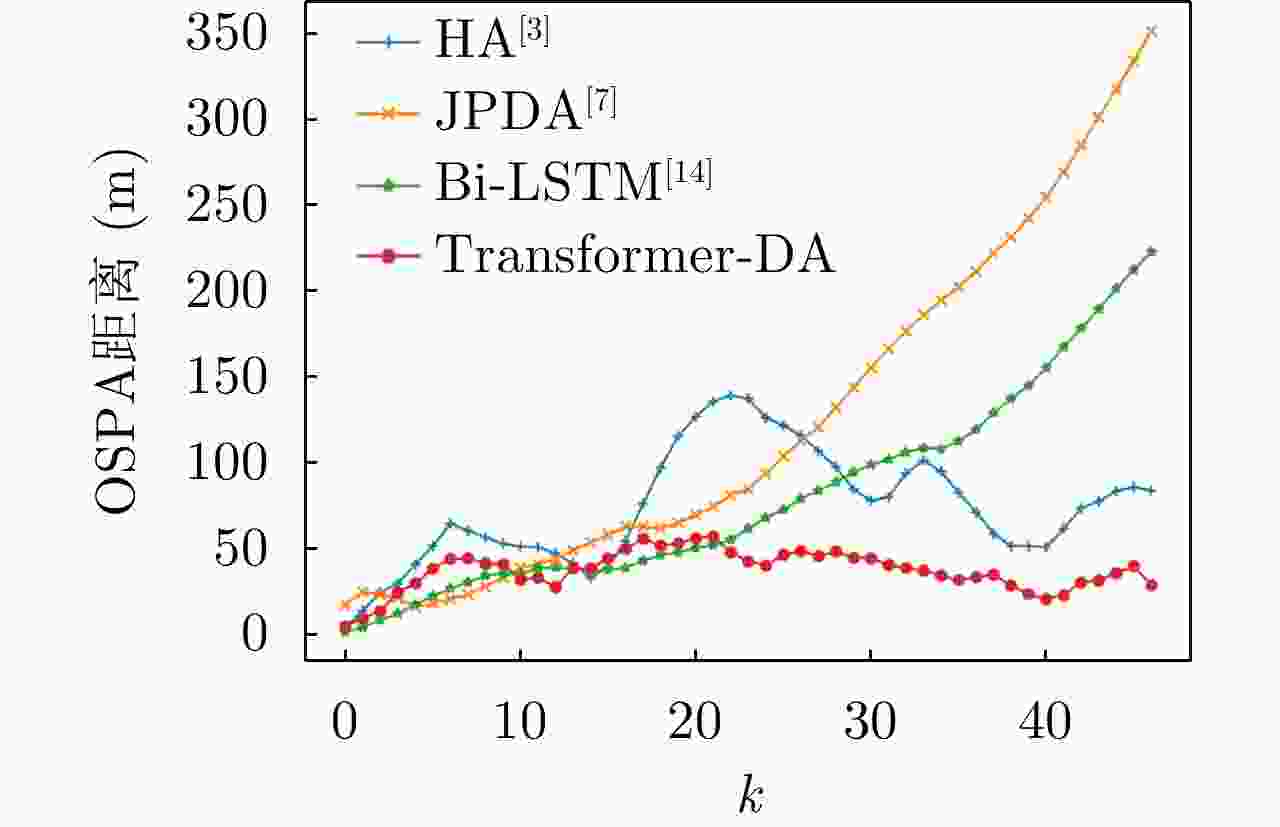
算法	${p_d} = 0.99$	${p_d} = 0.90$	${p_d} = 0.60$
HA	81.39	145.88	573.64
JPDA	159.38	217.10	487.70
Bi-LSTM	99.95	120.43	257.19
Transformer-DA	39.47	51.28	134.65

下载: 导出CSV

表 3 使用实际数据时算法在不同检测概率下的OSPA对比

Table 3. OSPA comparison of the algorithm under different detection probabilities when using actual data

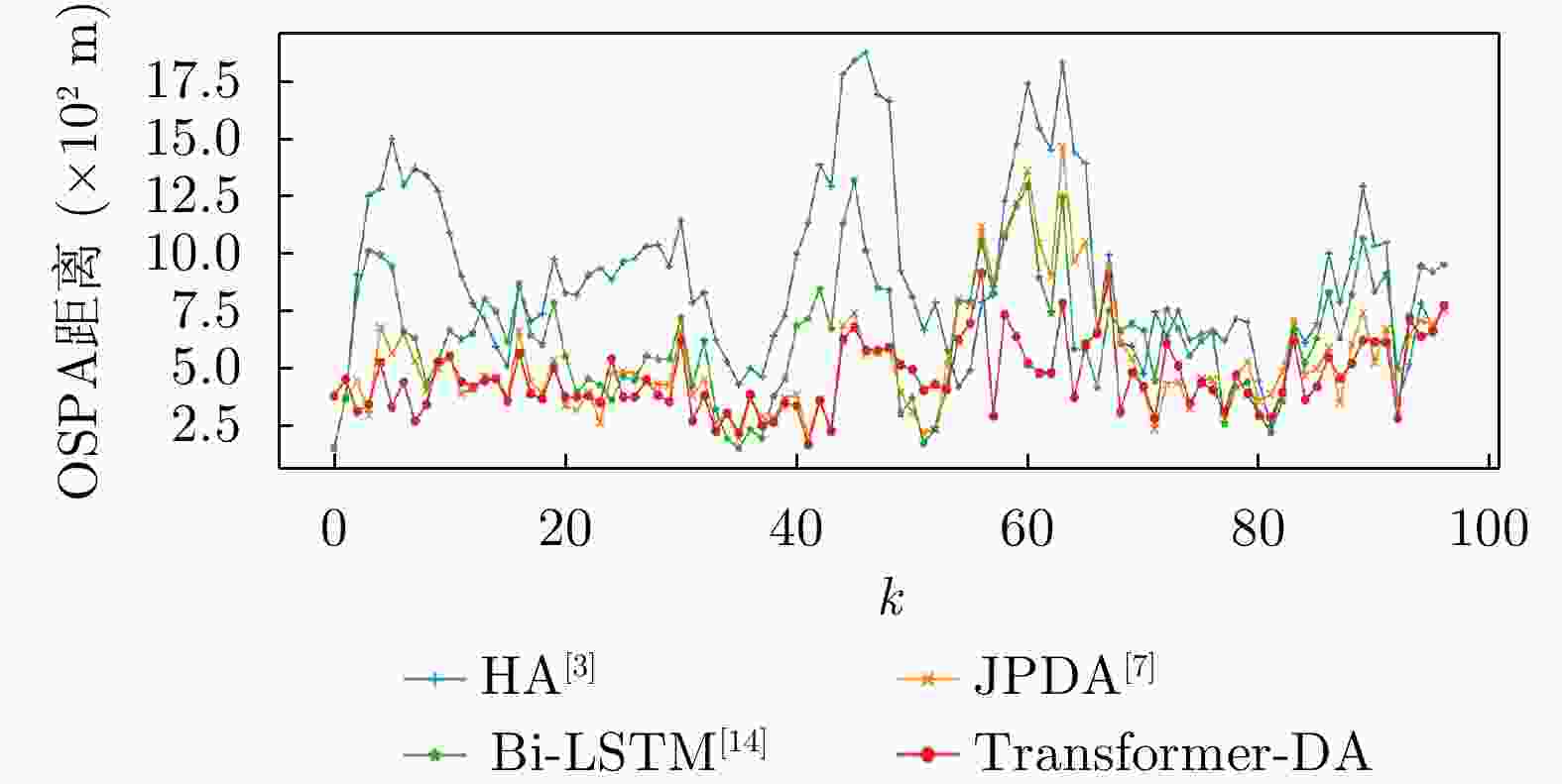
算法	${p_d} = 0.99$	${p_d} = 0.90$	${p_d} = 0.60$
HA	1000.76	1347.90	1859.65
JPDA	590.68	793.12	1319.21
Bi-LSTM	695.75	810.34	1256.33
Transformer-DA	481.91	587.63	923.10

下载: 导出CSV

表 4 不同检测概率下所提算法识别漏检目标的准确率(%)

Table 4. The accuracy of the proposed algorithm to identify missed targets under different detection probabilities (%)

实验类型	${p_d} = 0.90$	${p_d} = 0.60$
仿真数据实验	95.83	93.75
真实轨迹数据实验	95.91	89.90

下载: 导出CSV

参考文献(24)

[1]	BERTSIMAS D, SAUNDERS Z, and SHTERN S. Multitarget tracking via mixed integer optimization[J]. IEEE Transactions on Automatic Control, 2018, 63(11): 3627–3642. doi: 10.1109/TAC.2018.2832468
[2]	EMAMI P, PARDALOS P M, ELEFTERIADOU L, et al. Machine learning methods for solving assignment problem in multi-object tracking[J]. arXiv: 1802.06897, 2018.
[3]	WANG Jianguo, HE Peikun, and CAO Wei. Study on the Hungarian algorithm for the maximum likelihood data association problem[J]. Journal of Systems Engineering and Electronics, 2007, 18(1): 27–32. doi: 10.1016/S1004-4132(07)60045-0
[4]	ZHENG Le and WANG Xiaodong. Improved multiple hypothesis tracker for joint multiple target tracking and feature extraction[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 3080–3089. doi: 10.1109/TAES.2019.2897035
[5]	ZHANG Guangnan and LIU Penghui. Probabilistic data association algorithm based on modified input estimation[C]. 2011 7th International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, 2011: 1–4.
[6]	NI Longqiang, GAO Shesheng, and XUE Li. Improved probabilistic data association and its application for target tracking in clutter[C]. 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 2011: 293–296.
[7]	WANG Yuhuan, WANG Jinkuan, and WANG Bin. A modified multi-target tracking algorithm based on joint probability data association and Gaussian particle filter[C]. The 11th World Congress on Intelligent Control and Automation, Shenyang, China, 2014: 2500–2504.
[8]	HE Shaoming, SHIN H S, and TSOURDOS A. Joint probabilistic data association filter with unknown detection probability and clutter rate[C]. 2017 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Daegu, Korea, 2017: 559–564.
[9]	AINSLEIGH P L, LUGINBUHL T E, and WILLETT P K. A sequential target existence statistic for joint probabilistic data association[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 371–381. doi: 10.1109/TAES.2020.3018899
[10]	HOPFIELD J J and TANK D W. “Neural” computation of decisions in optimization problems[J]. Biological Cybernetics, 1985, 52(3): 141–152. doi: 10.1007/bf00339943
[11]	LEE M, XIONG Yuanhao, YU Guanding, et al. Deep neural networks for linear sum assignment problems[J]. IEEE Wireless Communications Letters, 2018, 7(6): 962–965. doi: 10.1109/LWC.2018.2843359
[12]	MILAN A, REZATOFIGHI S H, GARG R, et al. Data-driven approximations to NP-hard problems[C]. The Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, USA, 2017: 1453–1459.
[13]	LIU Huajun, ZHANG Hui, and MERTZ C. DeepDA: LSTM-based deep data association network for multi-targets tracking in clutter[C]. 2019 22th International Conference on Information Fusion (FUSION), Ottawa, Canada, 2019: 1–8.
[14]	VERMA R, RAJESH R, and EASWARAN M S. Modular multi target tracking using LSTM networks[EB/OL]. https://arxiv.org/abs/2011.09839, 2020.
[15]	VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]. Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, USA, 2017.
[16]	CHEN Yonghui and LI Huiying. DAM: Transformer-based relation detection for question answering over knowledge Base[J]. Knowledge-Based Systems, 2020, 201/202: 106077. doi: 10.1016/j.knosys.2020.106077
[17]	PILAULT J, LI R, SUBRAMANIAN S, et al. On extractive and abstractive neural document summarization with transformer language models[C]. The 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), 2020: 9308–9319.
[18]	ZHANG Qian, LU Han, SAK H, et al. Transformer transducer: A streamable speech recognition model with transformer encoders and RNN-T loss[C]. ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 2020: 7829–7833.
[19]	XU Yihong, BAN Yutong, DELORME G, et al. TransCenter: Transformers with dense queries for multiple-object tracking[EB/OL]. https://arxiv.org/abs/2103.15145v1, 2021.
[20]	SUN Peize, CAO Jinkun, JIANG Yi, et al. TransTrack: Multiple object tracking with Transformer[EB/OL]. https://arxiv.org/abs/2012.15460, 2021.
[21]	MEINHARDT T, KIRILLOV A, LEAL-TAIXE L, et al. Trackformer: Multi-object tracking with transformers[EB/OL]. https://arxiv.org/abs/2101.02702, 2021.
[22]	STORMS P P A and SPIEKSMA F C R. An LP-based algorithm for the data association problem in multitarget tracking[J]. Computers & Operations Research, 2003, 30(7): 1067–1085. doi: 10.1016/S0305-0548(02)00057-6
[23]	RISTIC B, VO B N, CLARK D, et al. A metric for performance evaluation of multi-target tracking algorithms[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3452–3457. doi: 10.1109/TSP.2011.2140111
[24]	马天力. 复杂环境下机载雷达多机动目标跟踪关键技术研究[D]. [博士论文], 西北工业大学, 2018. MA Tianli. Research on the key technology of multiple maneuvering targets tracking for airborne radar under complex environment[D]. [Ph. D. dissertation], Northwestern Polytechnical University, 2018.