-
摘要: 针对多目标突防组网雷达系统(NRS)场景,该文提出一种面向组网雷达干扰任务的多干扰机资源联合优化分配方法。首先,采用组网雷达在干扰环境中对目标的检测概率作为干扰性能指标;然后,结合不同突防目标的检测性能需求,建立了包含干扰波束和发射功率2个优化变量的资源优化模型,并利用粒子群算法对资源优化问题进行求解;最后,考虑到组网雷达系统参数不确定性带来的检测概率泛化误差,建立了干扰资源稳健优化分配模型。仿真结果表明,该文提出的优化方法能有效压制组网雷达,降低组网雷达对突防目标的检测概率;相比传统方法,稳健方法提升了多干扰机对组网雷达的协同干扰性能,且具有鲁棒性。Abstract: An optimal joint allocation of multijammer resources is proposed for jamming a Netted Radar System (NRS) in the case of multitarget penetration. First, the multitarget detection probabilities of NRS in the suppressive jamming environment are used as an interference performance metric. Then, the resource optimization model is established, including two optimization variables, namely, jamming beam and transmitting power, considering the detection performance requirements of different targets. Particle swarm optimization is used to solve the resource-optimization problem. Finally, considering the generalization error of the detection probability caused by the parameter uncertainty of the NRS, the robust resource-optimization model is established. The simulation results show that the proposed optimization model is effective in suppressing the NRS and reducing the probability of the penetrating targets detected by the NRS. Compared with the traditional method, the robust algorithm improves the cooperative interference performance of multiple jammers against NRS and is robust.
-
1. 引言
近年来,组网雷达系统(Netted Radar System, NRS)已受到了众多学者的广泛关注[1-4]。相比传统单基地雷达,组网雷达能实现多雷达的数据集成和资源共享,且不同雷达在工作方式、频段、空间覆盖范围等方面实现信息互补[2]。这些优势有利于组网雷达在电子对抗环境中实现反侦察,同时对隐身能力强的目标有更大的探测可能性[3]。因此,组网雷达具有更强的探测、跟踪、抗干扰和抗毁能力。
组网雷达已成为对抗电子干扰的重要手段,其复杂多样的组网特性使得传统的单干扰平台和一对一干扰方式即一个干扰机对一部雷达进行干扰,难以对其产生理想的干扰效果[5,6]。组网雷达给传统干扰手段带来严峻挑战,与之对抗的协同干扰技术逐渐发展起来。协同干扰是将多个干扰机进行组网,通过统一分配多干扰机的干扰时间、干扰功率、干扰样式等资源形成干扰能力更强的干扰体系,避免单干扰机在时间、功率和样式等方面的限制[5-8]。
在面向组网雷达的体系对抗中,多干扰机协同干扰更能满足干扰任务需求,也能提高目标成功突防组网雷达的概率。其中,实施协同干扰的一个关键环节就是资源分配,根据作战任务需求合理优化配置多个干扰机有限的资源,获得整个系统的最佳干扰效果。
国内外学者关于协同干扰资源调度的研究主要基于单波束干扰系统和多波束干扰系统[9-11]两大类。单波束干扰系统是指干扰机每一时刻只能产生单个波束去干扰一部雷达,而多波束干扰系统具有同时多目标干扰能力,它可以同时产生多个波束干扰多部雷达。文献[12-14]在单波束干扰系统的基础上,研究了多机协同干扰多目标的干扰资源分配问题;文献[6,15-17]是基于多波束干扰系统的协同干扰资源优化分配方法研究。上述文章提出的资源调度策略都是建立在干扰站波束发射功率均匀分配的前提条件下,通过优化波束指向实现最优干扰,均未考虑波束发射功率可控这一问题。进一步地,文献[18]针对单干扰机突防多目标的问题,提出了一种基于目标威胁等级优化分配波束发射功率的方法。文献[19]在多干扰站同时干扰多目标场景下,提出了一种基于目标威胁等级和发现概率下降程度自适应调整干扰机波束数量和波束指向的资源优化方法。
研究干扰资源调度问题还需考虑如何评估干扰策略的干扰效果,因此,选取合适的评估指标以及建立全面的干扰效果评估模型是必要的。对于压制性干扰,检测概率这一评估指标被广泛研究和应用[1,19-23]。文献[1]以雷达网检测概率作为评价指标,建立了针对干扰机编队多样式协同压制雷达网的干扰效果评估模型。文献[19]选取发现概率下降程度作为评估指标。文献[23]为提高协同干扰编队对雷达网的干扰效能,建立了基于雷达融合中心探测概率的干扰资源优化分配模型。考虑到监视雷达的首要任务是探测发现目标,因此选取雷达发现概率作为干扰性能指标是合理的。
总之,上述研究成果为提升多机协同干扰组网雷达的性能奠定了基础。但是,基于多波束干扰系统通过同时优化分配多干扰机波束和发射功率资源以提升干扰性能和资源利用率的问题还未受到关注。因此,本文针对多目标突防组网雷达的场景,提出了一种面向组网雷达干扰任务的多干扰机资源联合优化分配方法。首先,采用组网雷达在干扰环境中对目标的检测概率作为干扰性能指标;然后,结合不同目标的检测性能需求,建立了联合分配多干扰机波束和发射功率资源的优化问题,并用粒子群算法(Particle Swarm Optimization, PSO)分两步求解该优化问题;最后,考虑到组网雷达系统参数不确定性带来的检测概率泛化误差,建立了干扰资源稳健优化分配模型。仿真结果验证了本文所提资源优化分配方法以及稳健优化分配方法的有效性。
2. 系统模型
2.1 系统配置及约束
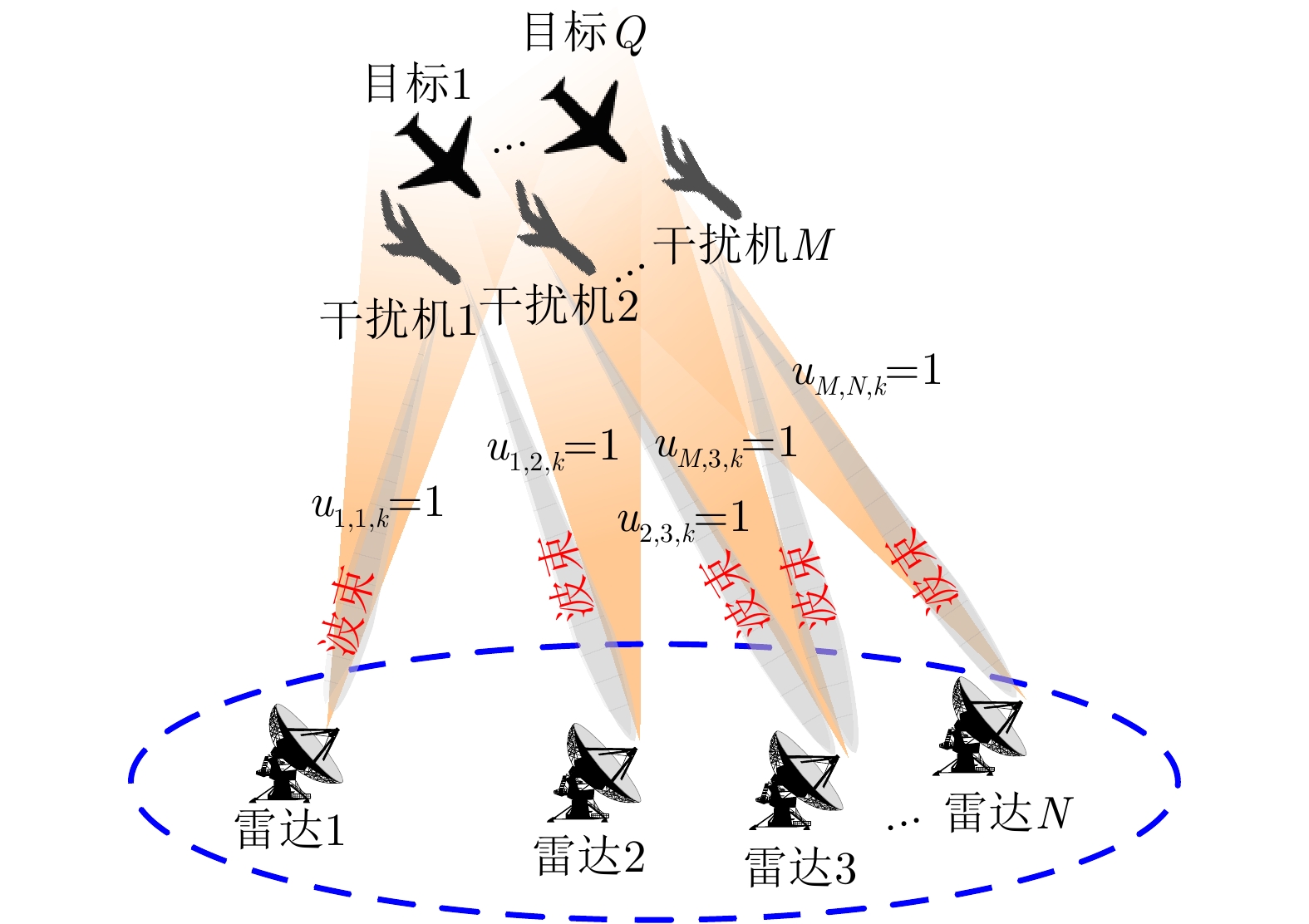
假设Q个目标执行突防组网雷达的任务,组网雷达系统由N部相控阵雷达组成。为提高目标成功突防的概率,
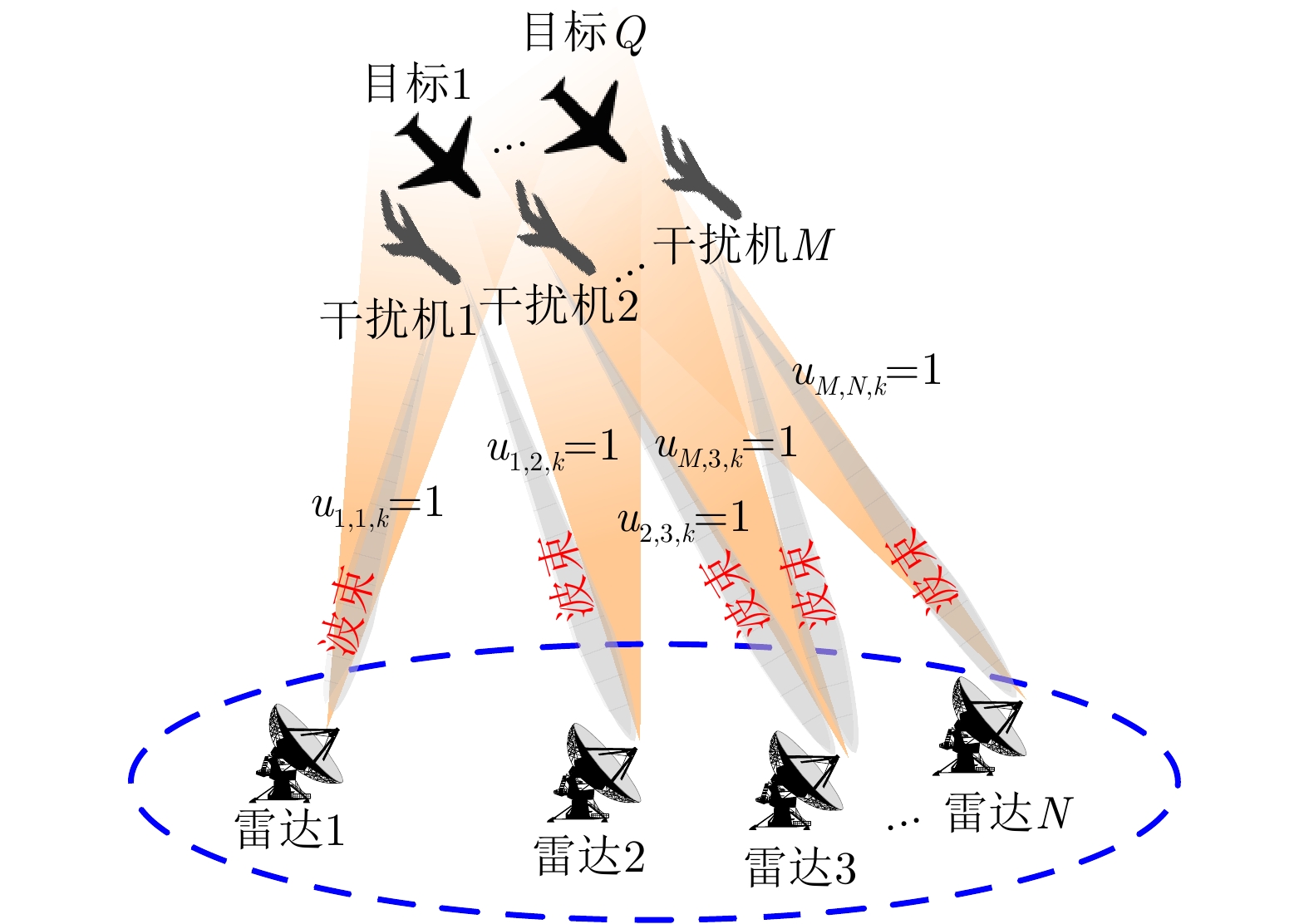
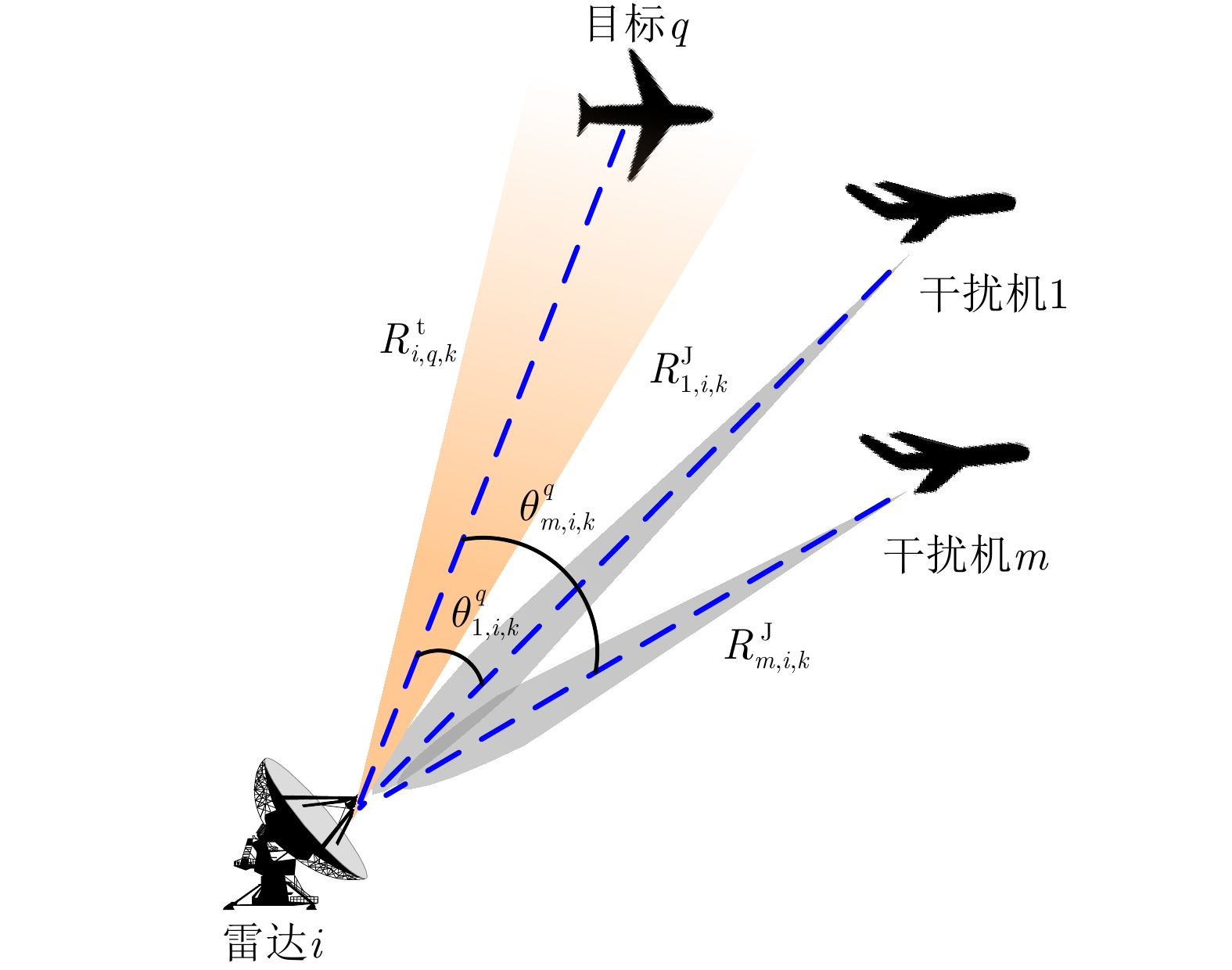
M(M<N) 个干扰机伴飞目标同时对组网雷达实施随队协同干扰,降低组网雷达对己方目标的探测跟踪性能。多机协同干扰的前提是已获得敌方各雷达的参数(如雷达位置、载频、脉宽、重频等),这些参数一般是通过电子侦察系统截获雷达发出的电磁信号,然后对其进行识别、分析和定位得到[24]。在图1所示的多目标突防组网雷达二维场景中,雷达
i(i=1,2,···,N) 的位置为(xi,yi) ,目标q(q=1, 2,···,Q) 在k 时刻的位置和速度分别为(xqk,yqk) 和(˙xqk,˙yqk) ,干扰机m(m=1,2,···,M) 在k 时刻的位置和速度分别为(xJm,k,yJm,k) 和(˙xJm,k,˙yJm,k) 。假设干扰机均采用多波束干扰系统[9-11],它可以产生多个功率可控的波束同时干扰多个雷达节点,但每个波束只能干扰一部雷达。考虑到波束指向的问题,本文引入干扰机
m 在k 时刻的波束指向向量umk=[um,1,kum,2,k···um,N,k]T ,其中,[⋅]T 表示转置运算,二元变量um,i,k 满足um,i,k={1, 干扰机m分配波束干扰雷达i0, 干扰机m未分配波束干扰雷达i (1) um,a,k≠um,b,k,a≠b (2) 式(2)表示每个干扰机最多分配一个波束去干扰同一部雷达。受系统限制,每个干扰机最多产生L个波束,即
N∑i=1um,i,k≤L (3) 为保证干扰波束资源被充分利用,所有雷达节点均能被干扰,因此分配给每部雷达的波束个数不超过S,即
1≤M∑m=1um,i,k≤S (4) 为了表示每个波束的可控发射功率,进一步定义干扰机m的波束发射功率向量
Pmk=[Pm,1,kPm,2,k··· Pm,N,k]T ,其中变量Pm,i,k 是波束um,i,k 对应的发射功率,且满足{Pm,i,k>0, 如果um,i,k=1Pm,i,k=0,如果um,i,k=0 (5) 式(5)表示如果干扰机
m 分配波束干扰雷达i ,则此波束的发射功率Pm,i,k 不为0;反之Pm,i,k=0 。每个波束的发射功率有最大功率Pmax 和最小功率{P_{\min }} 约束{P_{\min }} \le {P_{m,i,k}} \le {P_{\max }} (6) 且每个干扰机的总功率
P_m^{{\rm{total}}} 是一定的\sum\limits_{i = 1}^N {{P_{m,i,k}} = P_m^{{\rm{total}}}} (7) 当多干扰机协同干扰组网雷达时,可以用多个
{\boldsymbol{u}}_k^m 和{\boldsymbol{P}}_k^m 来描述整个干扰系统的波束指向和发射功率变量。{{\boldsymbol{u}}_k} = {\left[{\boldsymbol{u}}_k^1\;{\boldsymbol{u}}_k^2\; ··· \;{\boldsymbol{u}}_k^M\right]^{\rm{T}}}\quad (8) {{\boldsymbol{P}}_k} = {\left[{\boldsymbol{P}}_k^1\;{\boldsymbol{P}}_k^2\; ··· \;{\boldsymbol{P}}_k^M\right]^{\rm{T}}} (9) 2.2 干扰信号模型
雷达干扰是指干扰机通过发射干扰信号影响敌方雷达的检测、跟踪等性能,干扰分为压制性干扰和欺骗性干扰两种类型。协同压制干扰是多个干扰信号在雷达接收机处叠加,破坏雷达检测目标信息,起到联合干扰的效果。
本文主要采用噪声调频干扰,干扰机
m 对雷达i 施加的噪声调频干扰信号如式(10)所示。\begin{split} {j_{m,i,k}}(t) =\,& \sqrt {{P_{m,i,k}}} \exp \{ - {\rm{j}}2{\rm{\pi }}[{\omega _m}t \\ & {\rm{ + }}2{\rm{\pi }}{K_{{\rm{FM}}}}\int_0^t {u({t}'){\rm{d}}{t'} + \varphi ]} \} \end{split} (10) 其中,
u(t') 为调制噪声;\varphi 为相位函数;\sqrt {{P_{m,i,k}}} 为干扰信号振幅;{\omega _m} 为中心频率;{K_{{\rm{FM}}}} 为调频斜率。式(10)可变形为{j_{m,i,k}}(t) = \sqrt {{P_{m,i,k}}} {s_{m,i,k}}(t) (11) 其中,
{s_{m,i,k}}(t) 是干扰信号的归一化复包络。2.3 雷达回波信号模型
假设雷达采用自发自收的工作模式,它只会接收和处理自身发射并经目标散射的回波信号,且每部雷达在
k 时刻能发现我方的Q 个突防目标,那么雷达会接收到Q 个目标的回波信号。在协同压制干扰条件下,雷达还会接收到多个干扰机发射的干扰信号。因此,雷达i 的回波信号模型为{r_{i,k}}(t) = \underbrace {\sum\nolimits_{q = 1}^Q {{r_{i,q,k}}(t)} }_{({\rm{I}})} + \underbrace {\sum\nolimits_{m = 1}^M {j_{m,i,k}^{\rm{r}}(t)} }_{({\rm{II}})} + \underbrace {{w_{i,k}}(t)}_{({\rm{III}})} (12) 式(12)可以分为3部分,分别表示为
(I)
Q 个目标的回波信号:{r_{i,q,k}}(t) 是雷达i 接收到目标q 的回波信号{r_{i,q,k}}(t) = h_{i,q,k}^{}\sqrt {P_{i,q,k}^{\rm{r}}} z_{i,q,k}^{}(t - \tau _{i,q,k}^{})\exp ( - {\rm{j}}2{\rm{\pi }}f_{i,q,k}^{}t) (13) 其中,
h_{i,q,k}^{} 是目标q 的雷达横截面积;z_{i,q,k}^{}(t) 是雷达发射信号的归一化复包络;\tau _{i,q,k}^{} = 2R_{i,q,k}^{\rm{t}}/{{c}} 是由于目标q 与雷达i 之间的距离R_{i,q,k}^{\rm{t}} \!=\! \sqrt {(x_k^q \!-\! {x_i})_{}^2 \!+\! (y_k^q \!-\! {y_i})_{}^2} 导致的时延;{f_{i,q,k}} 是目标运动产生的多普勒频移;P_{i,q,k}^{\rm{r}} 是雷达i 接收到目标q 的回波信号功率[25,26],具体为P_{i,q,k}^{\rm{r}} = \frac{{P_i^{\rm{t}}G_i^{\rm{t}}G_i^{\rm{t}}{\lambda ^2_{\rm{f}}}h_{i,q,k}^{}}}{{{{(4{\rm{\pi }})}^3}{{(R_{i,q,k}^{\rm{t}})}^4}}} (14) 其中,
P_i^{\rm{t}} 是雷达i 的发射功率,G_i^{\rm{t}} 是雷达i 的发射天线增益;{\lambda _{\rm{f}}} 是雷达i 的工作波长。(II) M个干扰机发射的压制干扰信号:
j_{m,i,k}^{\rm{r}}(t) 是雷达i接收到干扰机m发射的压制干扰信号j_{m,i,k}^{\rm{r}}(t) = \sqrt {P_{m,i,k}^{\rm{J}}} {s_{m,i,k}}(t - \tau _{m,i,k}^{\rm{J}}) (15) 其中,
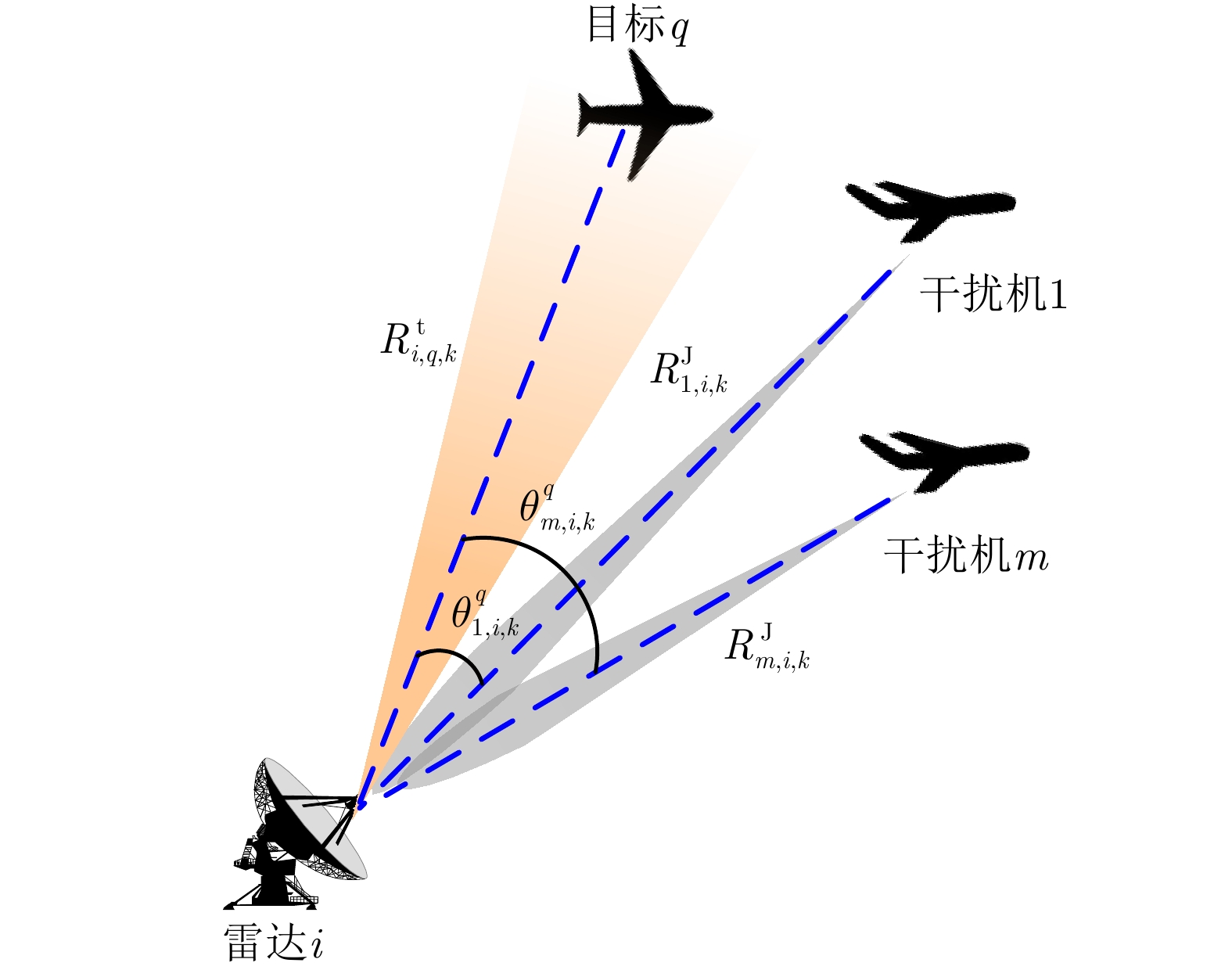
\tau _{m,i,k}^{\rm{J}} = R_{m,i,k}^{\rm{J}}/{{c}} 是由于雷达i 与干扰机m 之间的距离R_{m,i,k}^{\rm{J}} = \sqrt {(x_{m,k}^{\rm{J}} - {x_i})_{}^2 + (y_{m,k}^{\rm{J}} - {y_i})_{}^2} 导致的时延;P_{m,i,k}^{\rm{J}} 是雷达i 接收到来自干扰机m 发射的干扰信号功率[25,26]。\begin{split} P_{m,i,k}^{\rm{J}} \,& \triangleq P_{m,i,k}^{\rm{J}}(u_{m,i,k}^{},P_{m,i,k}^{},\theta _{m,i,k}^q) \\ & = \frac{{{u_{m,i,k}}P_{m,i,k}^{}G_m^{\rm{J}}\hat G_i^{\rm{t}}(\theta _{m,i,k}^q){\lambda^2_{\rm{f}}}{\gamma ^{\rm{J}}}}}{{{{(4{\rm{\pi }})}^2}{{(R_{m,i,k}^{\rm{J}})}^2}}} \end{split} (16) 其中,
G_m^{\rm{J}} 是干扰机m 的发射天线增益;{\gamma ^{\rm{J}}} 是极化失配损失;干扰机的工作波长{\lambda _{\rm{f}}} 与雷达一致;\hat G_i^{\rm{t}}(\theta _{m,i,k}^q) 是雷达i 在\theta _{m,i,k}^q 方向的天线增益;\theta _{m,i,k}^q 是干扰机m 的波束主瓣与雷达i 主瓣之间的夹角(此时雷达i 照射目标q )。k 时刻干扰机、雷达和目标的空间位置关系如图2所示。当干扰机实施随队干扰时,由于干扰机与目标空间位置分离,随队干扰信号既可以从雷达天线的主瓣进入雷达接收机(即主瓣干扰),也可以从雷达天线旁瓣进入(即旁瓣干扰)。雷达天线具有定向辐射的特点,式(16)中天线增益
\hat G_i^{\rm{t}}(\theta _{m,i,k}^q) 一般由经验公式给出[27,28]。\hat G_i^{\rm{t}}(\theta _{m,i,k}^q) = \left\{ \begin{aligned} & G_i^{\rm{t}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\quad\; 0 \le {\rm{|}}\theta _{m,i,k}^q{\rm{|}} \le \frac{{{\theta _{0.5}}}}{2} \\ & \beta {\left( {\frac{{{\theta _{0.5}}}}{{\theta _{m,i,k}^q}}} \right)^2}G_i^{\rm{t}},\;\;\;\frac{{{\theta _{0.5}}}}{2} < {\rm{|}}\theta _{m,i,k}^q{\rm{|}} \le {90^\circ }\;\; \\ & \beta {\left( {\frac{{{\theta _{0.5}}}}{{90}}} \right)^2}G_i^{\rm{t}},\;\;\;\;\;\;{90^\circ } < {\rm{|}}\theta _{m,i,k}^q{\rm{|}} \le {\rm{18}}{{\rm{0}}^\circ } \end{aligned} \right. (17) 其中,
{\theta _{0.5}} 为雷达天线波束宽度;常数\beta 通常取0.04~0.10。对于高增益、窄波束的天线,\beta \in [0.07, 0.10] ;对于低增益、宽波束天线,\beta \in [0.04,0.06] 。(III)
{w_{i,k}}(t) 是雷达接收机本身产生的噪声。雷达接收机的热噪声功率一般为{P_{\rm{n}}} = {{k}}{T_0}{B_{\rm{n}}}{F_{\rm{n}}} (18) 其中,
{P_{\rm{n}}} 是接收机内部热噪声功率;k 是玻尔兹曼常数;{T_0} 是雷达接收机的有效噪声温度;{B_{\rm{n}}} 是接收机带宽;{F_{\rm{n}}} 是接收机的噪声系数。2.4 协同压制干扰功率合成模型
假定各干扰机发射的干扰信号之间相互独立,当
M 个干扰机协同压制干扰单部雷达时,雷达接收的干扰信号总功率相当于各干扰信号功率之和。根据功率叠加原则,雷达i 在探测目标q 时接收到的总干扰信号功率P_{i,k}^{q,{\rm{total}}} 为P_{i,k}^{q{\rm{,total}}} = \sum\limits_{m = 1}^M {P_{m,i,k}^{\rm{J}}\left({u_{m,i,k}}{\rm{,}}{P_{m,i,k}}{\rm{,}}\theta _{m,i,k}^q\right)} (19) 3. 协同压制干扰组网雷达性能指标
3.1 协同压制干扰单部雷达检测概率模型
考虑到压制干扰的本质是使目标回波信号湮没在干扰信号中,降低雷达对目标的检测概率,且检测概率被众多学者用作衡量压制干扰性能的指标。因此,本文选取组网雷达对目标的检测概率作为干扰性能指标。本文计算检测概率是在假设电子侦察系统已获得敌方各雷达概略位置、部分工作频率与信号形式等参数信息,且不考虑单雷达欺骗干扰机的诱饵脉冲等变化情况。
在无干扰情况下,雷达
i 接收端的目标回波信噪比为\mu _{i,k}^q = \frac{{P_{i,q,k}^{\rm{r}}}}{{{P_{\rm{n}}}}} (20) 当雷达i受到压制干扰时,结合式(16)和式(19)可以计算目标q回波信干噪比为
\mu _{i,k}^q\; = \frac{{P_{i,q,k}^{\rm{r}}}}{{P_{i,k}^{q{\rm{,total}}} + {P_{\rm{n}}}}} (21) 由雷达检测原理可知,在背景噪声的统计分布以及目标起伏类型已确定的前提下,根据目标回波信干噪比可以计算雷达对目标的检测概率。我们以Swerling I型目标为例,计算雷达
i 对目标q 的检测概率[29,30]。{\rm{Pd}}_{i,k}^q = {{\rm{e}}^{\frac{{ - {V_{\rm{T}}}}}{{1 + \mu _{i,k}^q}}}} (22) 其中,
{V_{\rm{T}}} 是检测门限值。将(16)和式(19)代入式(22)可得{\rm{Pd}}_{i,k}^q \propto \dfrac{{P_{i,q,k}^{\rm{r}}}}{{\displaystyle\sum\limits_{m = 1}^M {\frac{{u_{m,i,k}^{}{P_{m,i,k}}G_m^{\rm{J}}\hat G_i^{\rm{t}}(\theta _{m,i,k}^q){\lambda^2_{\rm{f}}}{\gamma ^{\rm{J}}}}}{{{{(4{\rm{\pi }})}^2}{{(R_{m,i,k}^{\rm{J}})}^2}}}} + {P_{\rm{n}}}}} (23) 从式(23)看出,检测概率
{\rm{Pd}}_{i,k}^q 与u_{m,i,k}^{} 和{P_{m,i,k}} 两个变量有关。因此,通过联合优化分配干扰机的波束和功率资源,可以有效降低组网雷达对突防目标的检测概率,最大限度发挥有限干扰资源的效益。3.2 协同压制干扰组网雷达检测概率模型
考虑到在实际干扰作战中难以获知组网雷达的融合方式,本文假设组网雷达采用检测0/1信号融合方式,且组网雷达对目标检测概率的融合采用决策融合结构模型,融合中心采用K-N准则(也称秩K准则)。其具体内涵是:组网雷达中发现目标
q 的雷达节点数超过检测门限K(1 \le K \le N) 时,就判定组网雷达发现目标q ,否则判定未发现目标,如式(24)所示[31,32]。v_k^q = \left\{ \begin{gathered} 1{\rm{,}}\;\;\sum\limits_{i = 1}^N {v_{i,k}^q \ge K} \\ 0{\rm{,}}\;\sum\limits_{i = 1}^N {v_{i,k}^q} < K \\ \end{gathered} \right. (24) 其中,
v_k^q 表示组网雷达对目标q 的判决结果;v_{i,k}^q 表示雷达i 的判决结果且v_{i,k}^q \in {\rm{\{ 0,1\} }} 。根据K-N融合准则得到k时刻组网雷达对目标q的检测概率为[31,32]\begin{split} {\rm{Pd}}_k^q \,& \buildrel \Delta \over = {\rm{Pd}}_k^q(\boldsymbol{u}_k^{},\boldsymbol{P}_k^{}) \\ & =\! \sum\limits_{j = K}^N \!{\left\{\! {\sum\limits_{\forall \left\{ {\sum {v_{i,k}^q = j} } \right\}}\!\!\! {\mathop {\prod} \limits_i {{\left({\rm{Pd}}_{i,k}^q\right)}^{v_{i,k}^q}}\!\!{{\left(1 \!-\! {\rm{Pd}}_{i,k}^q\right)}^{1 - v_{i,k}^q}}} } \!\right\}} \end{split} (25) 其中,
\forall \left\{ {\displaystyle\sum {v_{i,k}^q} = j} \right\} 表示N 个雷达节点对目标q 的判决结果之和为j 的所有排列组合。组网雷达的检测性能是各雷达节点检测性能的多元函数,组网雷达采用不同的融合准则,检测概率有不同的数学表达式(见表1)。表 1 不同融合准则下的组网雷达检测概率Table 1. The detection probability of the NRS with different fusion rules融合准则 检测概率 AND准则(K = N) {\rm{Pd} }_k^q = {\displaystyle\prod\limits_{i = 1}^N } {\rm{Pd} }_{i,k}^q OR准则(K = 1) {\rm{Pd} }_k^q = 1 - \displaystyle\prod \limits^N_{i = 1} (1 - {\rm{Pd} }_{i,k}^q) 秩K准则 {\rm{Pd} }_k^q = \displaystyle\sum\limits_{j = K}^N {\left\{ {\sum\limits_{\forall \left\{ {\sum {v_{i,k}^q = j} } \right\} } {\mathop \prod \limits_i { {({\rm{Pd} }_{i,k}^q)}^{v_{i,k}^q} }{ {(1 - {\rm{Pd} }_{i,k}^q)}^{1 - v_{i,k}^q} } } } \right\} } 需要注意的是,本文后面建立的多干扰机资源联合优化分配模型在其他融合方式下也适用,只需根据不同的融合方式及融合准则修改检测概率模型即可,模型兼容性好。
3.3 协同压制干扰组网雷达的全局性能指标
组网雷达对
Q 个目标的检测概率形成的矢量{{\bf{P}}}{{{\bf{d}}}_k} ,可作为多干扰机协同压制干扰组网雷达的性能评估指标如式(26)所示。{\bf{P}}{{\bf{d}}_k} \buildrel \Delta \over = {\bf{P}}{{\bf{d}}_k}({\boldsymbol{u}}_k^{}{\rm{,}}{\boldsymbol{P}}_k^{}) = \left[{\rm{Pd}}_k^1\;{\rm{Pd}}_k^2\; ··· \;{\rm{Pd}}_k^Q\right] (26) 考虑到实际突防过程中,由于目标重要程度的差异,每个目标的检测概率需求会有所不同。多目标的检测概率需求矢量如式(27)所示。
{\boldsymbol{\omega}} _k = \left[\omega _k^1\;\omega _k^2\; ··· \;\omega _k^Q\right] (27) 其中,
\omega _k^q 是目标q 的检测概率需求。目标越重要,干扰方亟需保护该目标降低其被组网雷达发现的概率,因此\omega _k^q 也应越小。面向组网雷达干扰任务的多干扰机资源联合优化分配问题的本质是优化一个反映整体协同压制干扰任务有效性的全局代价函数。基于QoS原理[33],本文结合
{{\bf{P}}}{{{\bf{d}}}_k} 和{\boldsymbol{\omega }}_k 建立了全局代价函数。\mathbb{F}\Bigr[{{\bf{P}}}{{{\bf{d}}}_k}(\boldsymbol{u}_k^{},\boldsymbol{P}_k^{}),{{{{\boldsymbol{\omega}} _k}}}\Bigr] = \sum\limits_{q = 1}^Q {{\varPhi _q}\Bigr[{\rm{Pd}}_k^q(\boldsymbol{u}_k^{},\boldsymbol{P}_k^{}),\omega _k^q\Bigr]} (28) 其中,
{\varPhi _q}[{\rm{Pd}}_k^q(\boldsymbol{u}_k^{}{\rm{,}}\boldsymbol{P}_k^{}){\rm{,}}\omega _k^q] 是评估多干扰机随队干扰保护目标q 突防的任务有效性的代价函数,将其定义成指数形式为{\varPhi _q}\Bigr[{\rm{Pd}}_k^q(\boldsymbol{u}_k^{}{\rm{,}}\boldsymbol{P}_k^{}){\rm{,}}\omega _k^q\Bigr] = \exp \left[ {\frac{{{\rm{Pd}}_k^q(\boldsymbol{u}_k^{}{\rm{,}}\boldsymbol{P}_k^{})}}{{\omega _k^q}} - 1} \right] - 1 (29) 4. 多干扰机资源联合优化分配算法
4.1 干扰资源优化分配模型
从干扰系统设计来说,不考虑波束指向和发射功率调度虽简单易行,但当干扰资源有限时,资源的不合理配置会造成资源利用率低,甚至会造成干扰效果不理想。本文所提的面向组网雷达干扰任务的多干扰机资源联合优化分配方法旨在干扰资源有限的条件下,通过联合优化配置多干扰机的波束和功率资源,最小化组网雷达对突防目标的检测概率,其优化模型可建立为
\begin{aligned} & \mathop {\min }\limits_{\boldsymbol{u}_k^{}{\rm{,}}{\boldsymbol{P}_k}} \;\mathbb{F}[{\bf{P}}{{\bf{d}}_k}(\boldsymbol{u}_k^{}{\rm{,}}\boldsymbol{P}_k^{}){\rm{,}}{{{{\boldsymbol{\omega}} _k}}}]\\ & {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{aligned} &{P_{{\rm{min}}}} \le {P_{m,i{\rm{,}}k}} \le {P_{{\rm{max}}}}{\rm{,}}\;u_{m,i,k}^{}{\rm{ = 1}}\\ &P_{m,i,k}^{} = 0{\rm{,}}\;{u_{m,i,k}} = 0\\ &\sum\limits_{i = 1}^N {{P_{m,i{\rm{,}}k}}} = P_m^{{\rm{total}}}\\ &\sum\limits_{i = 1}^N {{u_{m,i{\rm{,}}k}}} \le L\\ &1 \le \sum\limits_{m = 1}^M {{u_{m,i{\rm{,}}k}}} \le S\\ &{u_{m,i{\rm{,}}k}} \ne {u_{m,j{\rm{,}}k}}{\rm{, }}\;i \ne j \end{aligned} \right. \end{aligned} (30) 从式(30)可以看出,本文实际建立了一个带干扰资源约束条件的数学优化问题。约束1和约束2表示波束和发射功率是相互耦合的;约束3表示每个干扰机有总功率限制;约束4表示每个干扰机产生的波束个数不超过L;约束5表示每部雷达均能被干扰,且最多受到S个波束的干扰;约束6表示每个干扰机在干扰同一雷达节点时最多分配一个波束。
4.2 求解干扰资源优化分配模型
式(30)优化问题由于以下原因很难得到其最优解:(i)含有二元变量
{u_{m,i,k}} \in {\rm{\{ 0,1\} }} ,故它是非凸的;(ii)波束指向变量{u_{m,i{\rm{,}}k}} 和发射功率变量{P_{m,i{\rm{,}}k}} 是相互耦合的,且两者总是以乘积的形式出现,同时求解比较困难。于是本文提出了基于粒子群算法(Particle Swarm Optimization, PSO)的两步求解方法,具体步骤如下:(1) 基于波束发射功率均匀分配求解波束指向结果
\boldsymbol{u}_k^{{\rm{opt}}} :假设干扰机m能同时干扰所有雷达节点,且每个波束的发射功率均匀分配\boldsymbol{P}_k^{m{\rm{,uni}}} = (P_m^{{\rm{total}}}/N) \cdot {\bf{1}}_{N \times 1}^{} 。由于波束指向变量\boldsymbol{u}_k^{} 是一个二元变量,为求解方便,将其松弛为[0,1] 区间内的连续随机变量\boldsymbol{u}_k^{{\rm{con}}} \!=\! \left[\!\! {\begin{array}{*{20}{c}} {\boldsymbol{u}_k^{1,{\rm{con}}}} \\ \vdots \\ {\boldsymbol{u}_k^{M,{\rm{con}}}} \end{array}} \!\!\right] \!=\! \left[\!\!\! {\begin{array}{*{20}{c}} {u_{1,1,k}^{{\rm{con}}}}\!\!&\!\!{u_{1,2,k}^{{\rm{con}}}}\!\!&\!\! ··· \!\!&\!\!{u_{1,N,k}^{{\rm{con}}}} \\ \vdots\!\! &\!\! \vdots \!\!&\!\! {\rm{}} \!\!&\!\! \vdots \\ {u_{M,1,k}^{{\rm{con}}}}\!\!&\!\!{u_{M,2,k}^{{\rm{con}}}}\!\!& \!\!··· \!\!&\!\!{u_{M,N,k}^{{\rm{con}}}} \end{array}} \!\!\!\right] (31) 结合式(31),优化问题变为
\begin{split} & \mathop {\min }\limits_{\boldsymbol{u}_k^{{\rm{con}}}} \;\mathbb{F}[{\bf{P}}{{\bf{d}}_k}(\boldsymbol{u}_k^{{\rm{con}}}{\rm{,}}\boldsymbol{P}_k^{{\rm{uni}}}){\rm{,}}{{{{\boldsymbol{\omega}} _k}}}]\\ & {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;0 \le u_{m,i,k}^{{\rm{con}}} \le 1 \end{split} (32) 用PSO算法求解式(32)得到松弛结果
\boldsymbol{u}_{k,{\rm{opt}}}^{{\rm{con}}} ,并将波束指向结果初始化\boldsymbol{u}_k^{{\rm{opt}}}{\rm{ = }}{{\bf{0}}_{M \times N}} 。找到\boldsymbol{u}_{k,{\rm{opt}}}^{{\rm{con}}} 中的最大值并用0替换,并将最大值对应位置的波束指向结果u_{m,i,k}^{{\rm{opt}}} 置为1,同时判断\boldsymbol{u}_k^{{\rm{opt}}} 是否满足式(2)—式(4)所示的约束条件,如果不满足则u_{m,i,k}^{{\rm{opt}}}{\rm{ = }}0 。重复上述步骤,直到M个干扰机的所有波束资源全部用尽,最终得到波束指向最优分配方式\boldsymbol{u}_k^{{\rm{opt}}} ,详细求解过程见表2。表 2 基于PSO的波束指向\boldsymbol{u}_k^{{\rm{opt}}} 求解方法Table 2. The solution algorithm of the beam selection\boldsymbol{u}_k^{{\rm{opt}}} based on PSO步骤1 初始化\boldsymbol{P}_k^{{\rm{uni}}}, \boldsymbol{u}_k^{{\rm{opt}}}{\rm{ = }}{{\bf{0}}_{M \times N}}, \boldsymbol{u}_k^{{\rm{con}}} \in [0,1]; 步骤2 PSO求解式(32),得到松弛结果\boldsymbol{u}_{k,{\rm{opt}}}^{{\rm{con}}}; 步骤3 循环l = 1, 2,··· ,L \times M
寻找最大值[{m_l},{i_l}] = \arg \;\max \{ \boldsymbol{u}_{k,{\rm{opt}}}^{{\rm{con}}}\} ;
更新\boldsymbol{u}_k^{{\rm{opt}}}({m_l},{i_l}) = 1,且\boldsymbol{u}_{k,{\rm{opt}}}^{{\rm{con}}}({m_l},{i_l}) = 0;
判断\boldsymbol{u}_k^{{\rm{opt}}}是否满足式(2)—式(4)的约束条件,若不满足则
\boldsymbol{u}_k^{{\rm{opt}}}({m_l},{i_l}) = 0;
循环结束步骤4 输出波束指向结果\boldsymbol{u}_k^{{\rm{opt}}}。 (2) 在
\boldsymbol{u}_k^{{\rm{opt}}} 基础上求解发射功率分配结果\boldsymbol{P}_k^{{\rm{opt}}} :在步骤(1)得到波束指向结果\boldsymbol{u}_k^{{\rm{opt}}} 的基础上,优化问题变为\begin{split} & \mathop {\min }\limits_{{\boldsymbol{P}_k}} \;\mathbb{F}[{\bf{P}}{{\bf{d}}_k}(\boldsymbol{u}_k^{{\rm{opt}}}{\rm{,}}\boldsymbol{P}_k^{}){\rm{,}}{{{{\boldsymbol{\omega}} _k}}}]\\ & {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{aligned} & {P_{{\rm{min}}}} \le {P_{m,i{\rm{,}}k}} \le {P_{{\rm{max}}}}{\rm{,}}\;u_{m,i,k}^{{\rm{opt}}}{\rm{ = 1}}\\ & P_{m,i,k}^{} = 0{\rm{,}}\;u_{m,i,k}^{{\rm{opt}}} = 0\\ & \sum\limits_{i = 1}^N {{P_{m,i{\rm{,}}k}}} = P_m^{{\rm{total}}} \end{aligned} \right. \end{split} (33) 同样地,用PSO求解式(33)得到
\boldsymbol{P}_k^{{\rm{opt}}} 。4.3 组网雷达参数不确定性模型
4.1节干扰资源优化分配模型是建立在完全获得组网雷达系统参数的理想情况下,但实际干扰作战中,电子侦察系统一般无法精确获得组网雷达系统的各雷达位置等参数信息,同时难以获得组网雷达的融合方式以及融合准则,只能利用参数估计。受限于参数估计精度,3.1节和3.2节计算得到的检测概率相比目标真实检测概率存在泛化误差,前面提出的优化分配算法可能会出现性能下降问题。因此,本节考虑了组网雷达参数不确定性,并提出了干扰资源稳健优化分配算法。
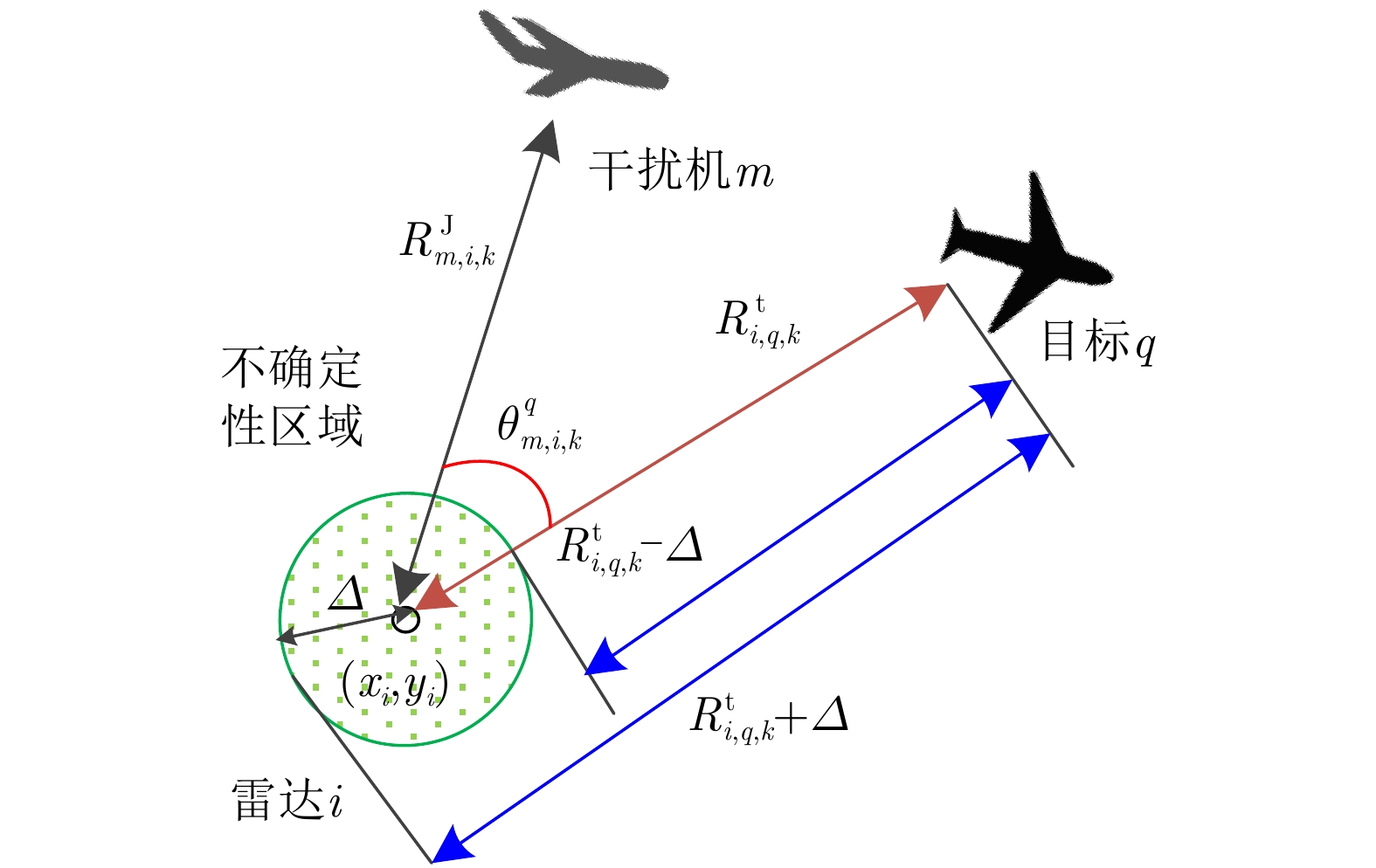
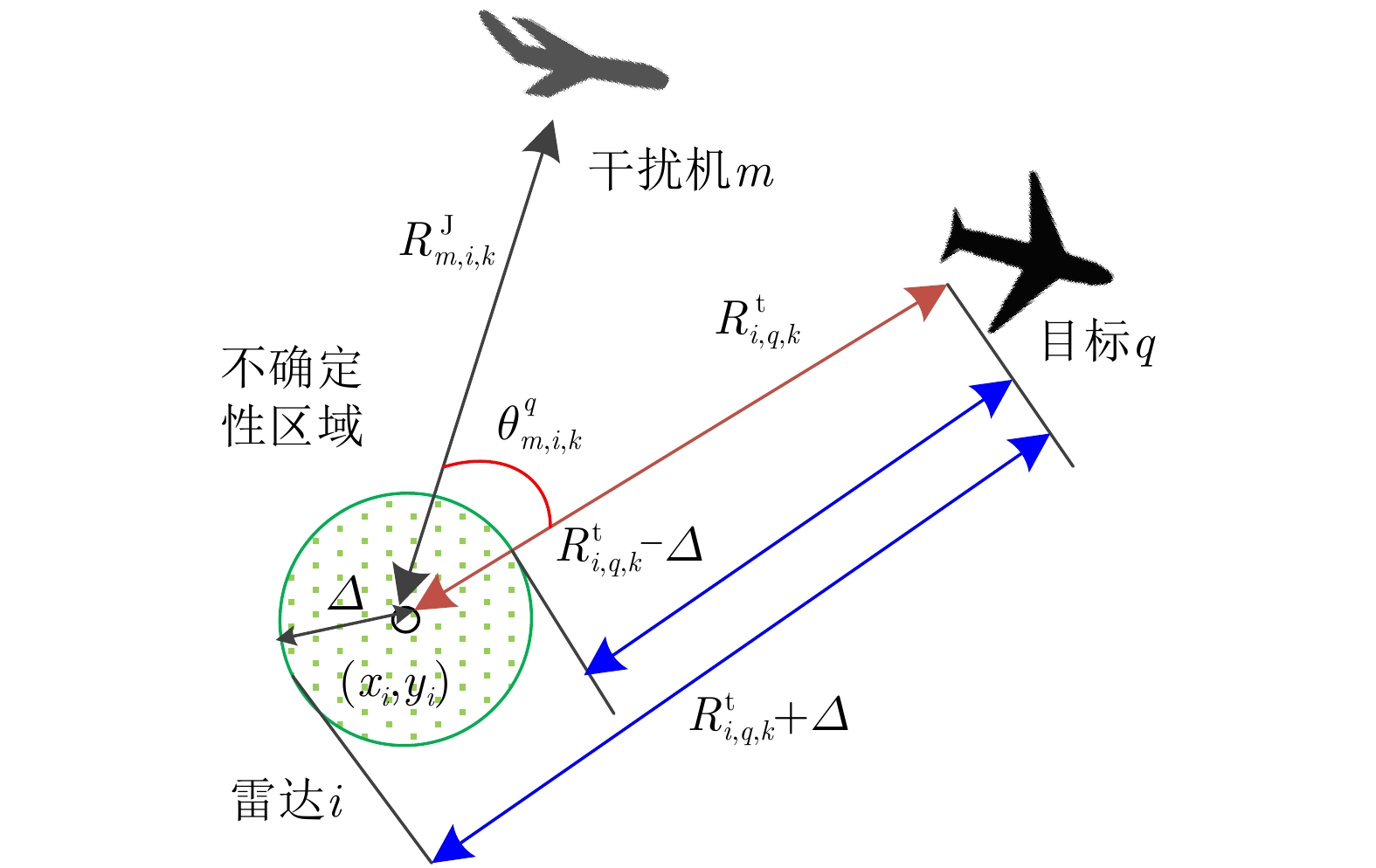
首先考虑雷达位置不确定性,雷达
i 的不确定位置在一个不确定性区域内,假设将此不确定性区域表示为如图3所示的不确定性圆。{({\tilde x_i} - {x_i})^2} + {({\tilde y_i} - {y_i})^2} \le {\varDelta ^2} (34) 其中,
({\tilde x_i},{\tilde y_i}) 表示雷达i 的不确定位置,\varDelta 为不确定性圆的半径。雷达位置不确定性会带来距离不确定性,距离不确定性受限于整个不确定性圆,其可以表示为线性不确定区间。
\tilde R_{i,q,k}^{\rm{t}} \in \left[ {R_{i,q,k}^{\rm{t}}{\rm{ - }}\varDelta {\rm{,}}R_{i,q,k}^{\rm{t}}{\rm{ + }}\varDelta } \right]\;\; (35) \tilde R_{m,i,k}^{\rm{J}} \in \left[ {R_{m,i,k}^{\rm{J}}{\rm{ - }}\varDelta {\rm{,}}R_{m,i,k}^{\rm{J}}{\rm{ + }}\varDelta } \right] (36) 其中,
\tilde R_{i,q,k}^{\rm{t}} 表示雷达i 与目标q 之间的不确定距离,\tilde R_{m,i,k}^{\rm{J}} 表示雷达i 与干扰机m 之间的不确定距离。雷达位置不确定性也会带来角度不确定性,角度不确定性线性区间为\tilde \theta _{m,i,k}^q \in \left[ {{{\theta_{\!\!\!\! \_}}_{{m,i,k}}^q} {\rm{,}}\bar \theta _{m,i,k}^q} \right] (37) 其中,
\tilde \theta _{m,i,k}^q 表示不确定角度,\bar \theta _{m,i,k}^q 和{\theta_{\!\!\!\!\_}} _{{m,i,k}}^q 分别表示角度不确定性的上界和下界。由表1知,组网雷达在不同K-N融合准则下对目标的检测概率也是不同的,所以还应该考虑融合准则不确定性,将其建为一个集合
\tilde \varOmega 。\tilde \varOmega \in \left\{ {{\rm{1 }}{\text{-}}N{\rm{,2 }}{\text{-}}N{\rm{,}} ··· {\rm{,}}N{\text{-}}N} \right\} (38) 整个组网雷达系统参数不确定性可表示为
\left\{ {\tilde R_{i,q,k}^{\rm{t}}{\rm{,}}\tilde R_{m,i,k}^{\rm{J}}{\rm{,}}\tilde \theta _{m,i,k}^q{\rm{,}}\tilde \varOmega } \right\} \in {\varXi _k} (39) 结合
{\varXi _k} ,组网雷达在压制干扰条件下对目标q 的检测概率不确定性模型为\begin{split} {{\tilde{\rm{P}} {\rm{d}}}}_k^q \;& \triangleq {{\tilde{\rm{P}} {\rm{d}}}}_k^q(\boldsymbol{u}_k^{}{\rm{,}}\boldsymbol{P}_k^{}{\rm{|}}{\varXi _k})\\ & = \!\!\sum\limits_{j = K}^N \!\!{\left\{ {\sum\limits_{\forall \left\{ {\sum {v_{i,k}^q = j} } \right\}} {\mathop {\prod} \limits_i {{\left({{\tilde{\rm{P}} {\rm{d}}}}_{i,k}^q\right)}^{v_{i,k}^q}}\!{{(1 \!-\! {{\tilde {\rm{P}}{\rm{d}}}}_{i,k}^q)}^{1 \!-\! v_{i,k}^q}}} } \right\}} \end{split} (40) 其中,
{{\tilde {\rm{P}}{\rm{d}}}}_{i,k}^q 是考虑组网雷达参数不确定性时雷达i 对目标q 的检测概率。将
{{\tilde{\bf P}}}{{{\bf{d}}}_k} \triangleq {{\tilde{\bf P}}}{{{\bf{d}}}_k}(\boldsymbol{u}_k^{}{\rm{,}}\boldsymbol{P}_k^{}) = [{{\tilde {\rm{P}}{\rm{d}}}}_k^1\;{{\tilde {\rm{P}}{\rm{d}}}}_k^2\; ··· \;{{\tilde {\rm{P}}{\rm{d}}}}_k^Q] 作为4.4小节干扰资源稳健优化分配算法的性能指标。4.4 干扰资源稳健优化分配模型
基于组网雷达参数不确定性的干扰资源稳健优化分配算法,旨在提高干扰系统在组网雷达参数不确定情况下的协同干扰性能。结合已有的最大最小化准则[34,35],稳健分配等效于最小化最差参数时的目标检测概率,确保在参数最差时多干扰机也能有效压制组网雷达。数学上可将稳健分配表述为最小化最大的
\mathbb{F}[{\tilde{\bf P}}{{\bf{d}}_k}(\boldsymbol{u}_k^{}{\rm{,}}\boldsymbol{P}_k^{}){\rm{,}}{{{{\boldsymbol{\omega}} _k}}}] ,即\begin{split} & \mathop {\min }\limits_{\boldsymbol{u}_k^{}{\rm{,}}{\boldsymbol{P}_k}} \;\mathop {\max }\limits_{\left\{ {\tilde R_{i,q,k}^{\rm{t}},\tilde R_{m,i,k}^{\rm{J}}{\rm{,}}\tilde \theta _{m,i,k}^q{\rm{,}}\tilde \varOmega } \right\} \in {\varXi _k}} \;\mathbb{F}[{\tilde{\bf P}}{{\bf{d}}_k}(\boldsymbol{u}_k^{}{\rm{,}}\boldsymbol{P}_k^{}){\rm{,}}{{\boldsymbol{\omega}} _k}]\\ & {\rm{s}}{\rm{.t}}{\rm{. }}\;\;\;\;\;\;\;\;\;\;\;\;{\rm{(30)}}\\[-10pt] \end{split} (41) 其中,
\mathbb{F}[{\tilde{\bf P}}{{\bf{d}}_k}(\boldsymbol{u}_k^{}{\rm{,}}\boldsymbol{P}_k^{}){\rm{,}}{{{{\boldsymbol{\omega}} _k}}}] 是考虑组网雷达参数不确定性的全局代价函数。参数最差是指组网雷达对目标检测概率最大时对应的参数不确定性集合\varXi _k^{\max } 。例如,只考虑距离不确定性时,由式(14)、式(16)和式(22)可知,检测概率{{\tilde {\rm{P}}{\rm{d}}}}_{i,k}^q 与\tilde R_{i,q,k}^{\rm{t}} 的四次方成反比,与\tilde R_{m,i,k}^{\rm{J}} 的二次方成正比,故最差参数集合是\varXi _k^{\max } = \left\{ {\tilde R_{i,q,k}^{\rm{t}} = R_{i,q,k}^{\rm{t}}{\rm{ - }}\varDelta {\rm{,}}\tilde R_{m,i,k}^{\rm{J}} = R_{m,i,k}^{\rm{J}}{\rm{ + }}\varDelta } \right\} 。之后,式(41)的求解方法同4.2节。5. 仿真结果与分析
本节通过仿真实验将本文算法与传统算法、稳健算法进行比较,验证本文所提方法的有效性。传统方法是所有干扰机采用单波束干扰系统且资源配置方式固定,即干扰机1干扰雷达1,干扰机2干扰雷达3,干扰机3干扰雷达5。稳健算法仅考虑雷达2位置不确定性带来的距离不确定性
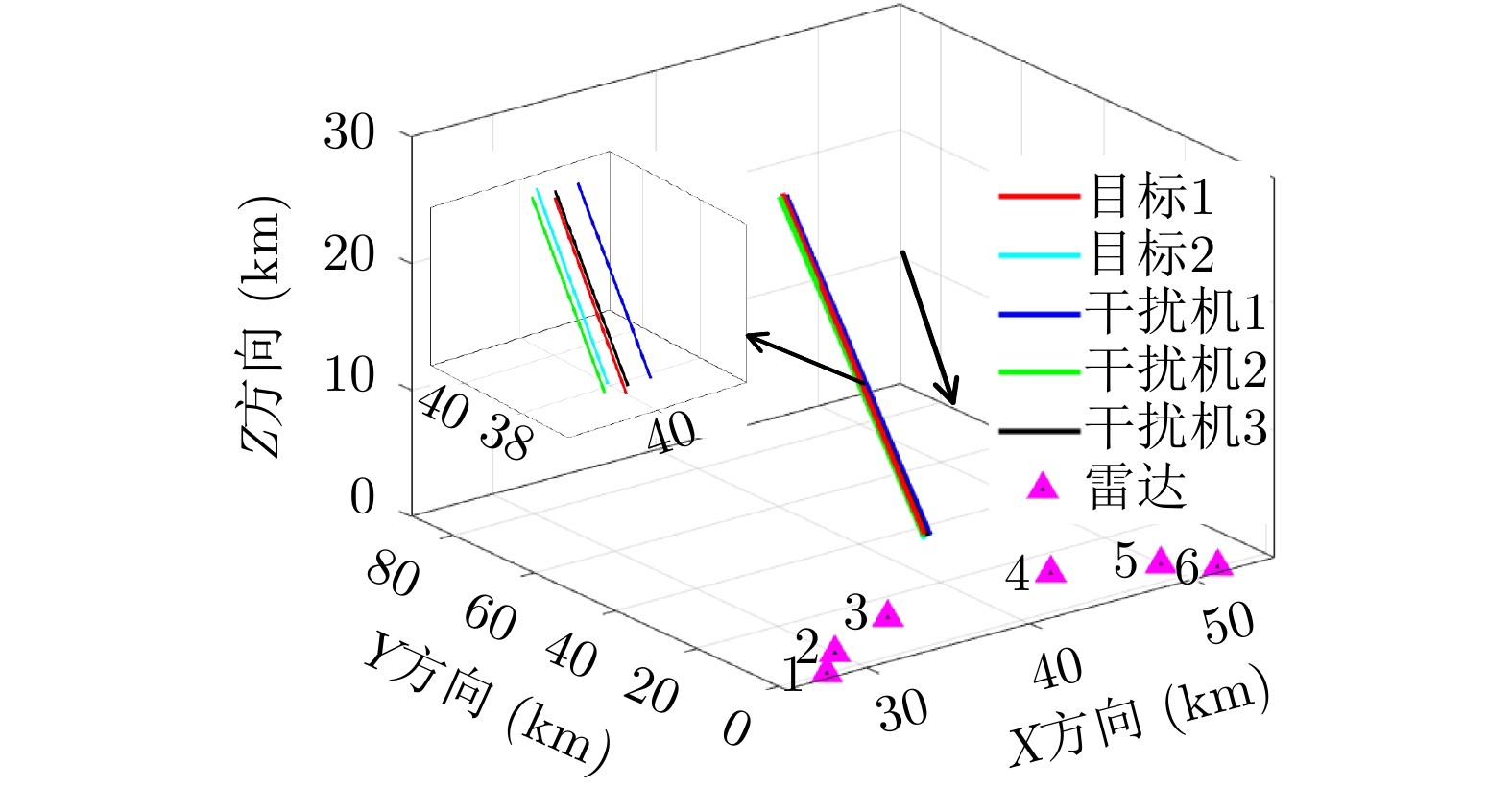
\tilde R_{i,q,k}^{\rm{t}} 和\tilde R_{m,i,k}^{\rm{J}} ,其中不确定性圆的半径\varDelta = 0.5 km。考虑
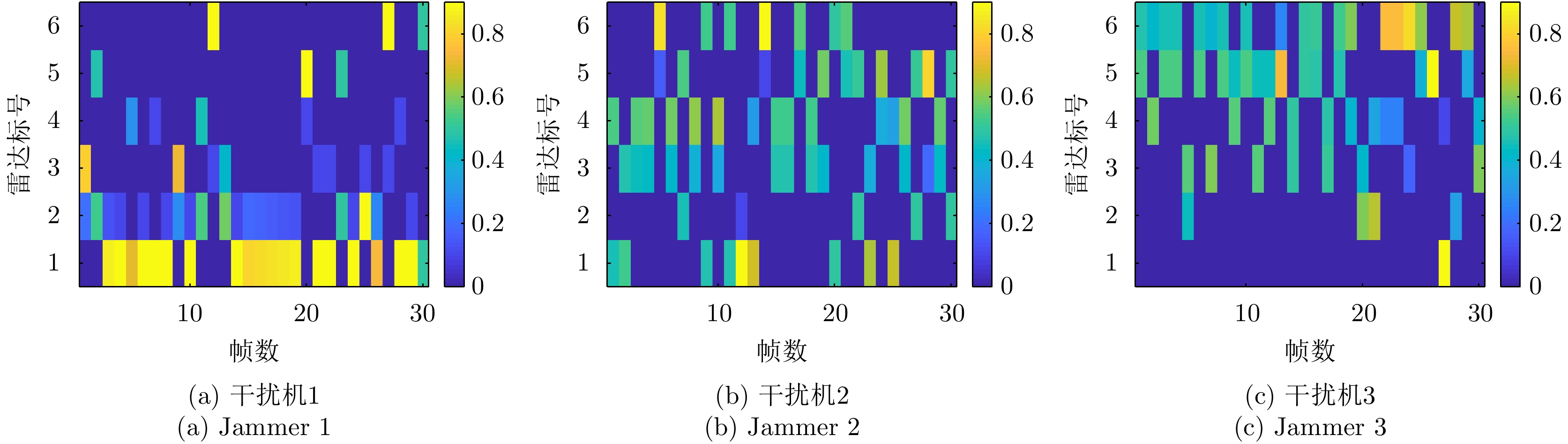
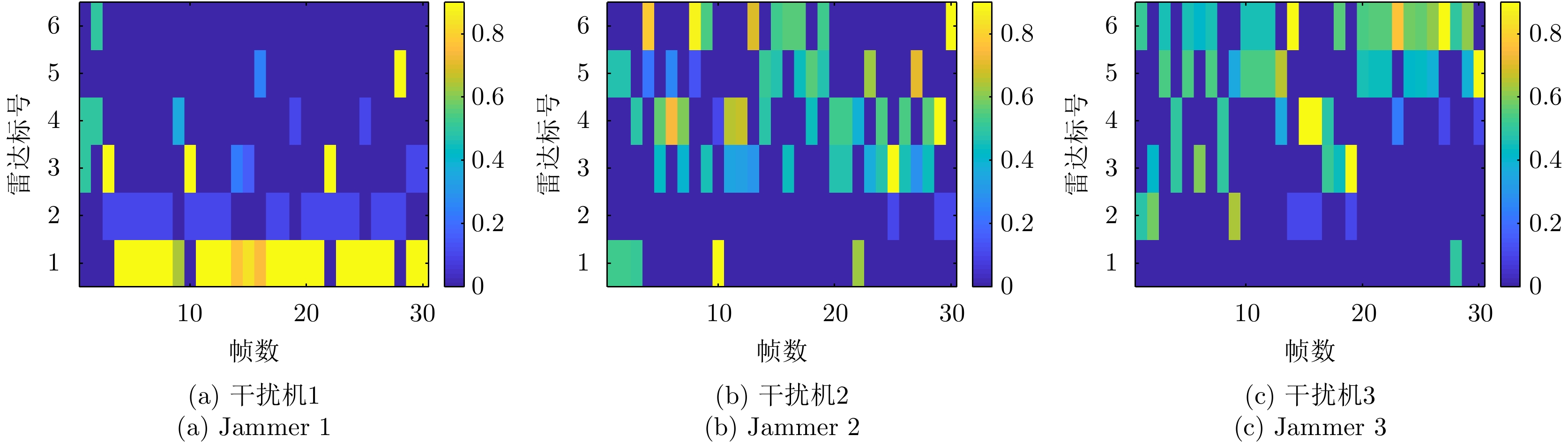
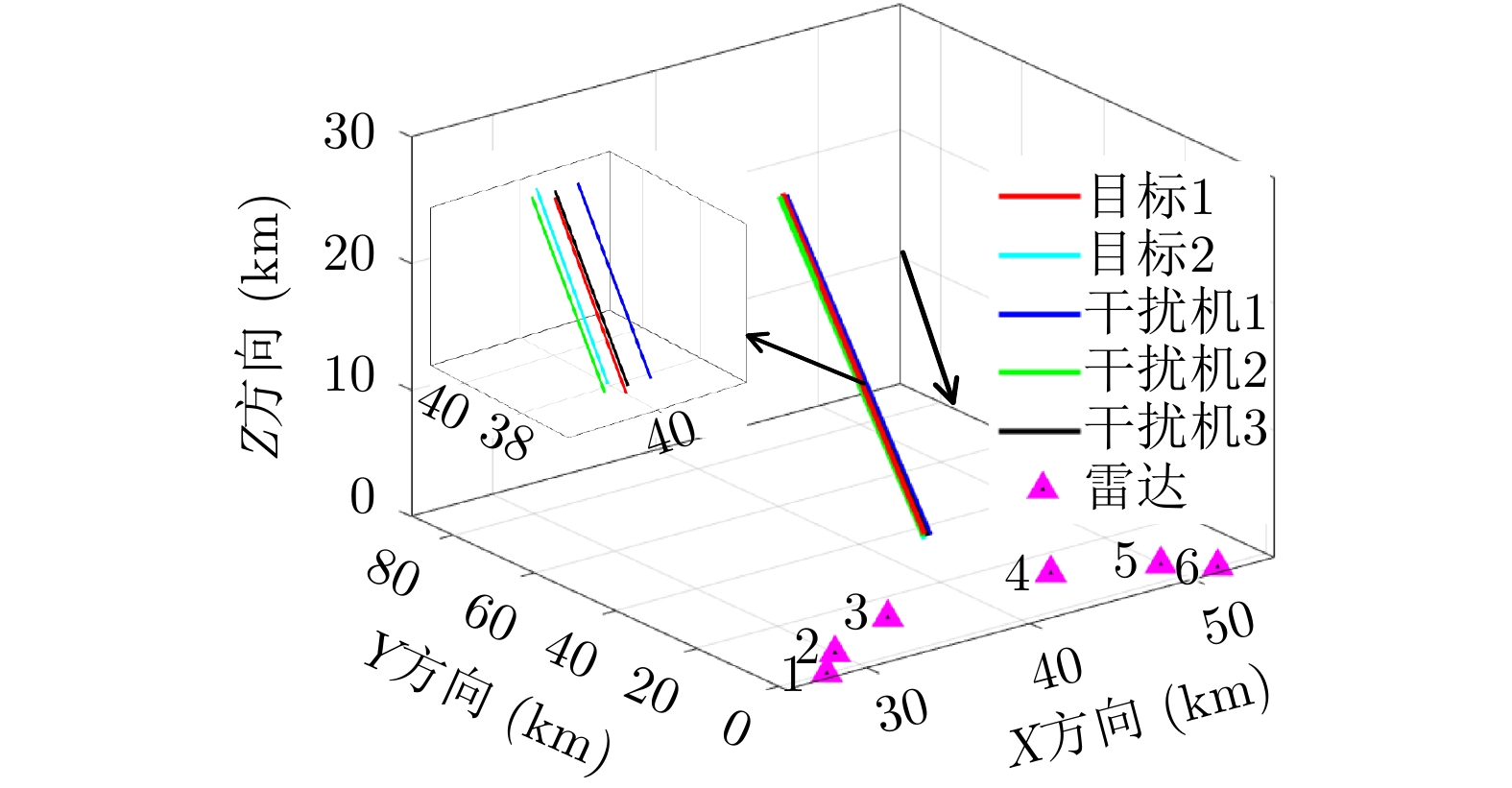
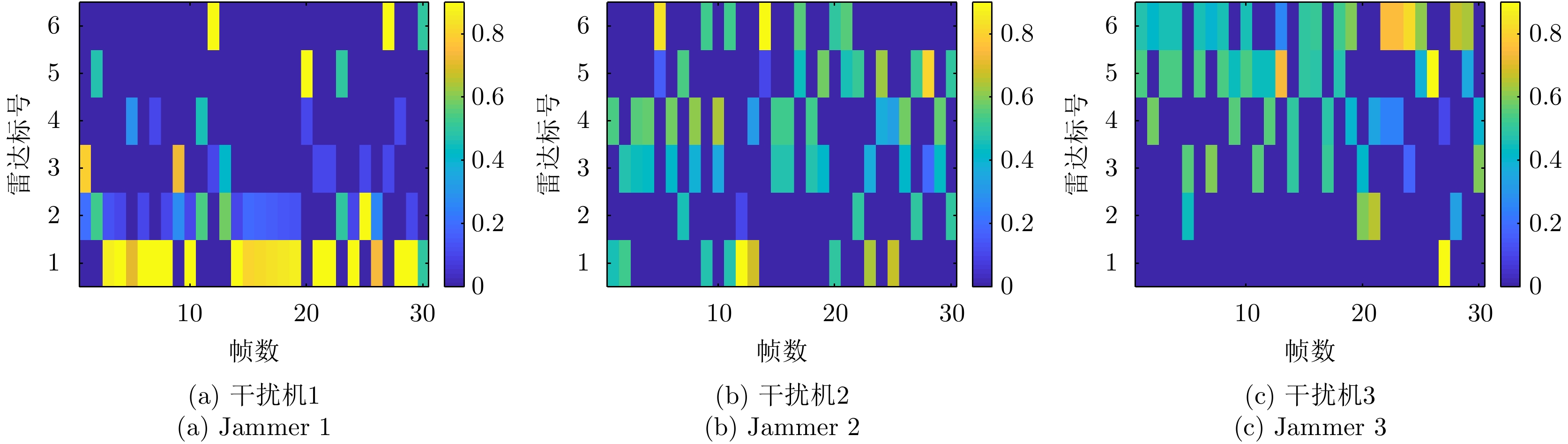
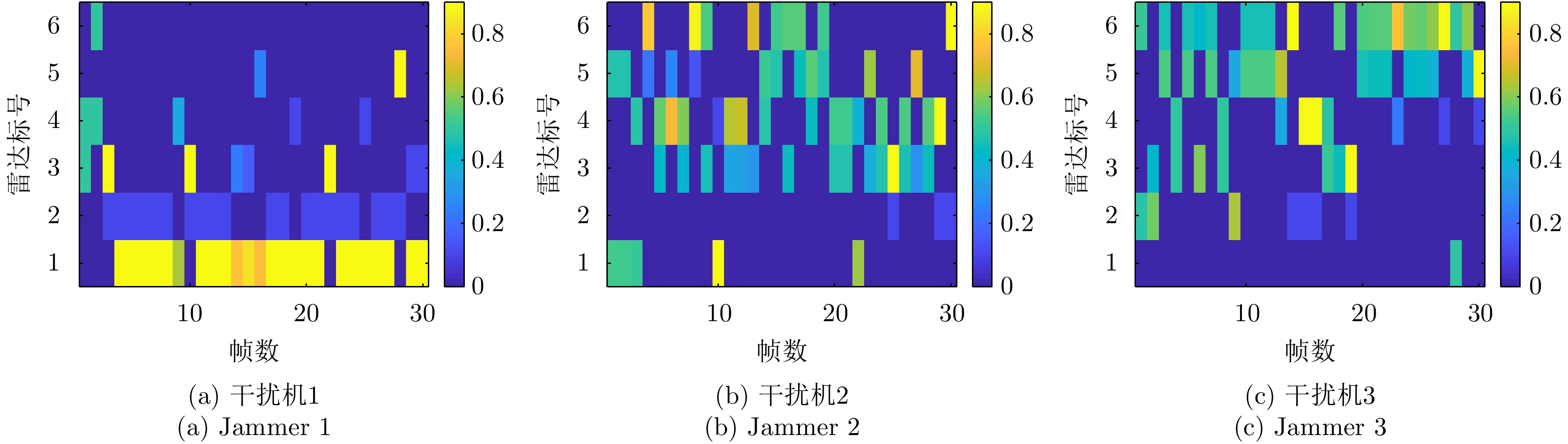
Q = 2 个目标突防组网雷达系统,M = 3 个干扰机实施随队干扰。假设已知组网雷达系统由N = 6 部雷达组成,融合中心采用秩4准则。每个干扰机和每部雷达的参数均相同,分别如表3和表4所示。目标RCS均为{h_{i,q,k}} = 1 m2,检测概率需求为{{{{\boldsymbol{\omega}} _k}}} = [0.4\;0.4] 。干扰机波束发射功率的上下限分别为{P_{\max }} = 0.9P_m^{{\rm{total}}} 和{P_{\min }} = 0.1P_m^{{\rm{total}}} 。利用PSO求解式(32)和式(33)时,相关参数设置:粒子数为100,总迭代次数为30,学习因子均为2,在第\kappa 次迭代时惯性权值\varpi = 0.9 - 0.5*(\kappa /50) 。多干扰机随队干扰保护目标突防的运动轨迹和组网雷达的空间位置关系如图4所示。表 3 干扰机工作参数Table 3. The working parameters of the jammer参数 数值 干扰机总功率P_m^{{\rm{total}}} 130 W 波束个数L 2 天线增益G_m^{\rm{J}} 10 dB 极化失配损失{\gamma ^{\rm{J}}} 0.5 工作波长{\lambda _{\rm{f}}} 0.1 m 天线波瓣宽度{\theta _{0.5}} 3° 表 4 雷达工作参数Table 4. The working parameters of the radar node参数 数值 发射功率P_i^{\rm{t}} 200 MW 最多被干扰波束个数S 1 发射天线增益G_i^{\rm{t}} 40 dB 虚警概率 10–6 工作波长{\lambda _{\rm{f}}} 0.1 m 图5和图6分别是优化算法和稳健算法的资源分配结果,图中不同的颜色代表不同的功率值。为了方便比较,将功率分配结果进行归一化处理。
\bar P_{m,i,k}^{{\rm{opt}}} = \frac{{P_{m,i,k}^{{\rm{opt}}}}}{{P_m^{{\rm{total}}}}} (42) 其中,
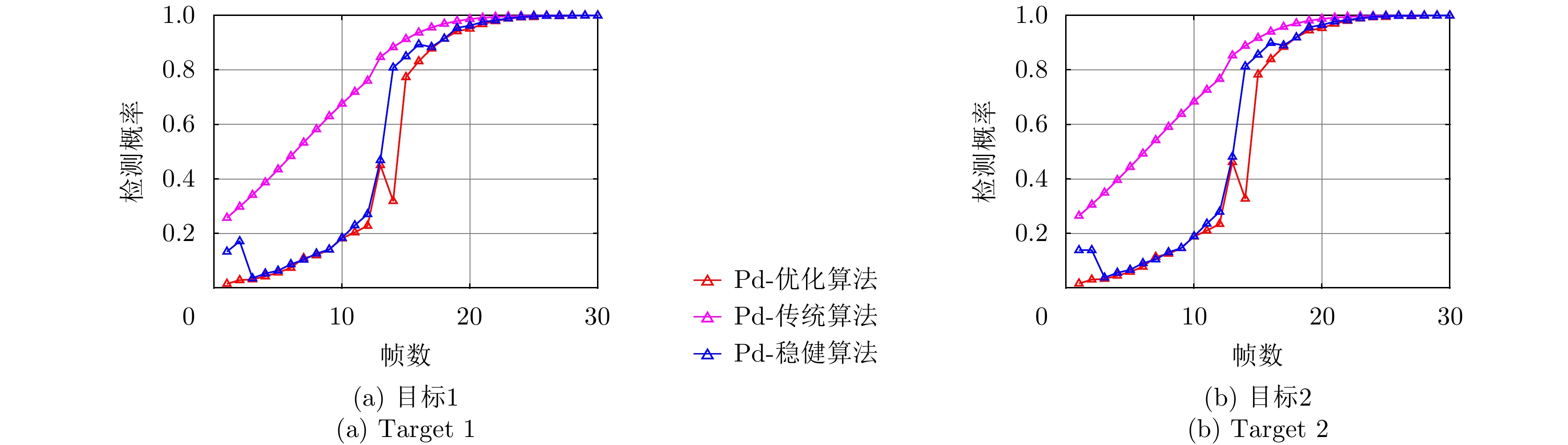
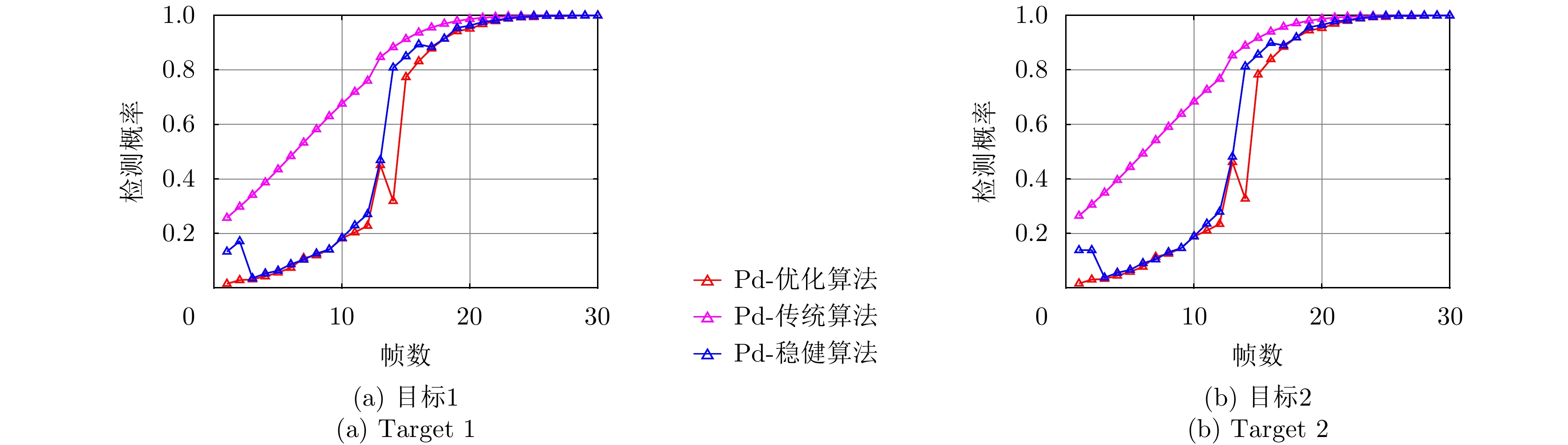
\bar P_{m{\rm{,}}i{\rm{,}}k}^{{\rm{opt}}} \in [0,1] ,若归一化功率值\bar P_{m,i,k}^{{\rm{opt}}} 为0,代表干扰机m 未分配波束干扰雷达i 。对比图5(a)和图6(a)、图5(b)和图6(b)以及图5(c)和图6(c)可以看出,相比优化算法,稳健算法将较少功率资源分配给雷达节点2且分配的功率基本为{P_{\min }} 。稳健算法优先分配功率资源给不确定性小的雷达节点,对不确定性大的雷达节点分配较少功率,以保证整体干扰性能。因此,稳健算法着重避免参数不确定性,有较好的鲁棒性。图7给出了3种资源配置方式下组网雷达对两个突防目标的检测概率。两个目标的检测概率基本一致是因为两个目标距离较近,相对于各雷达节点的空间位置差异性不明显。从图7(a)和图7(b)看出,相比传统资源配置方式,干扰资源经优化分配和稳健优化分配后两个目标的检测概率明显降低,这证明了本文所提两种方法均能有效压制组网雷达,提升整个干扰系统的性能。只考虑距离不确定性时,相比优化算法,通过稳健算法得到的两个目标检测概率较大,说明了距离不确定性会影响干扰效果。
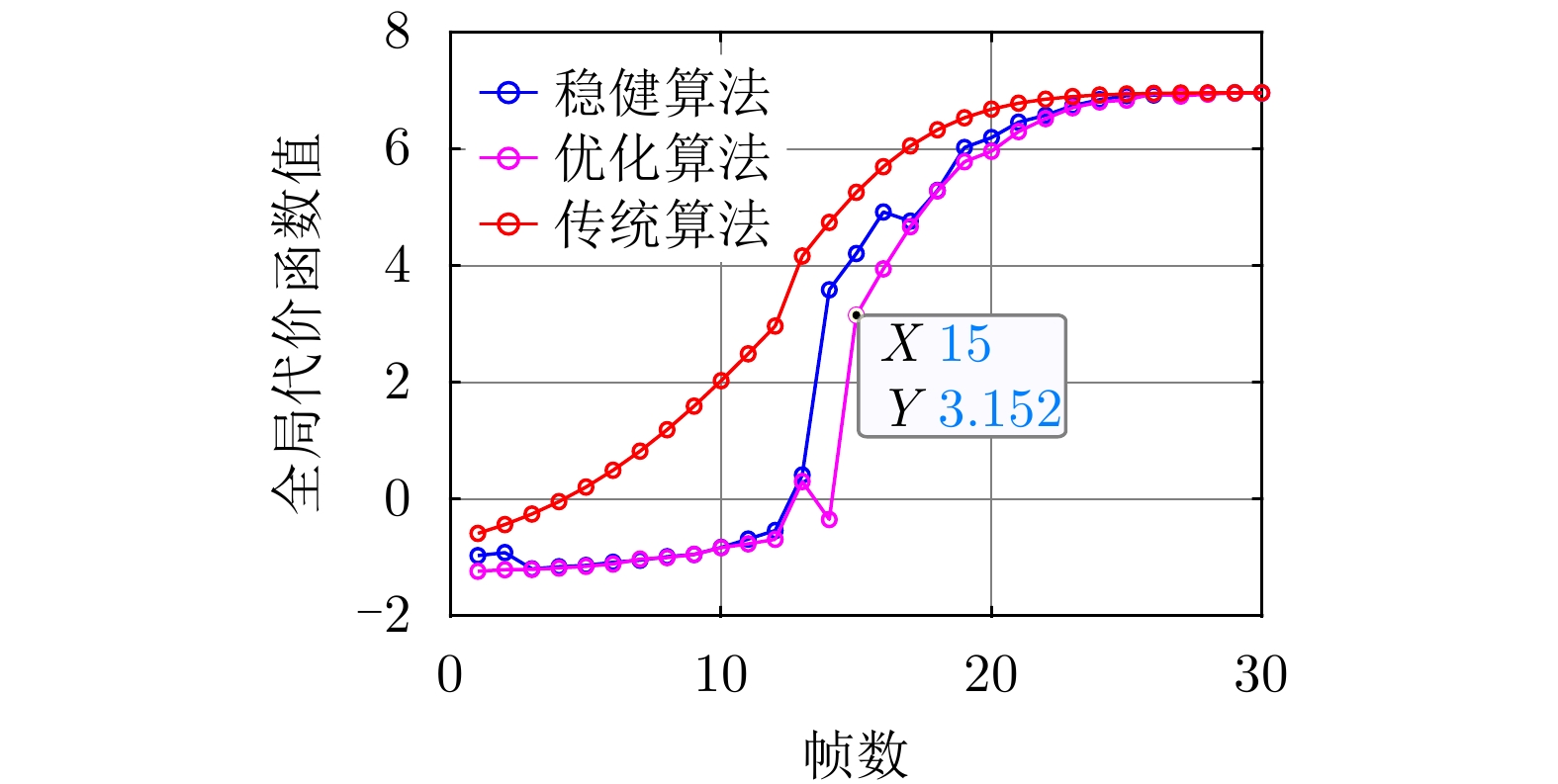
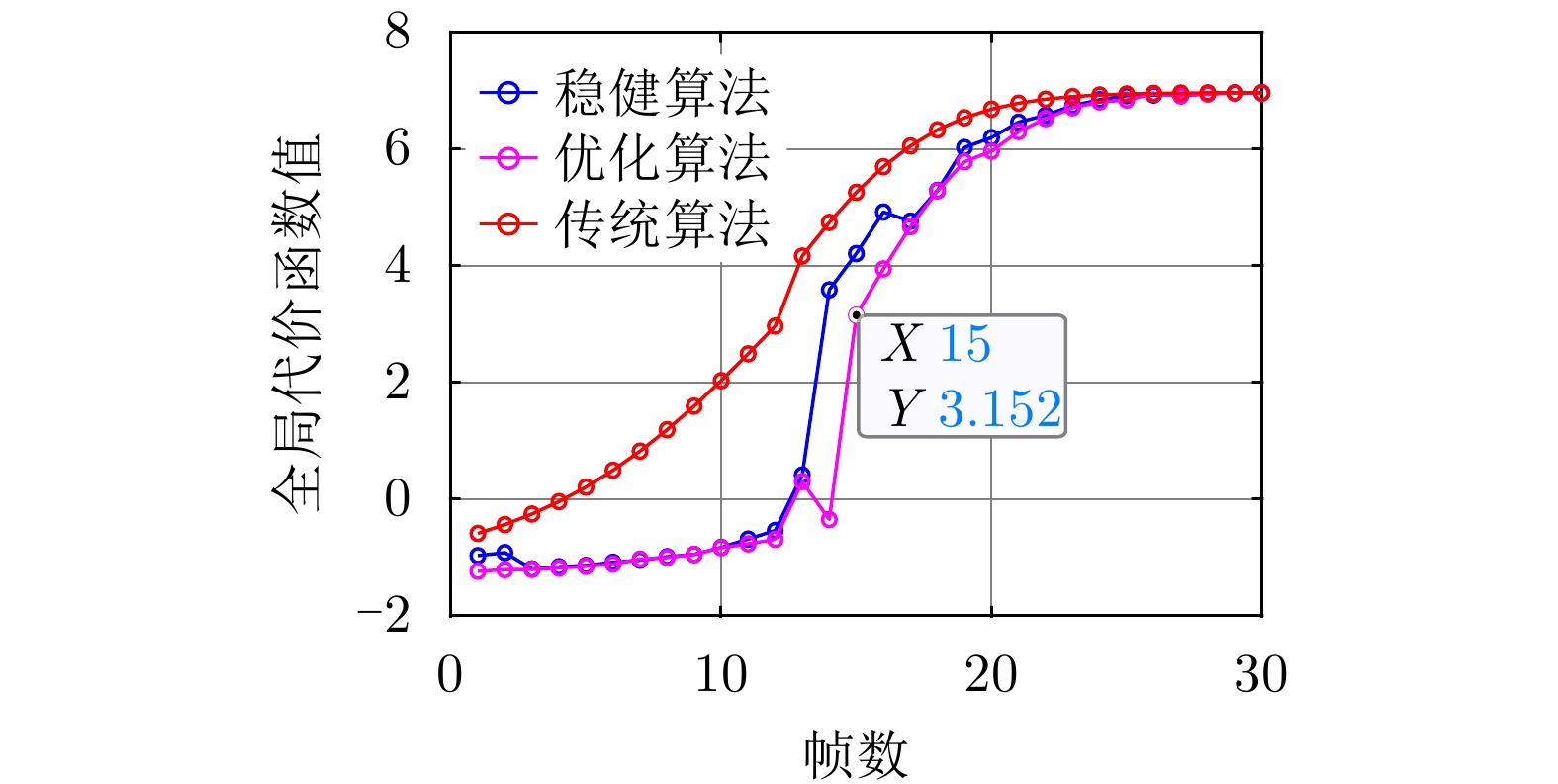
图8是优化算法与传统算法、稳健算法的全局代价函数值对比图。由图8可见,本文所提优化算法和稳健算法的全局代价函数值更小,进一步验证了本文所提方法的有效性。
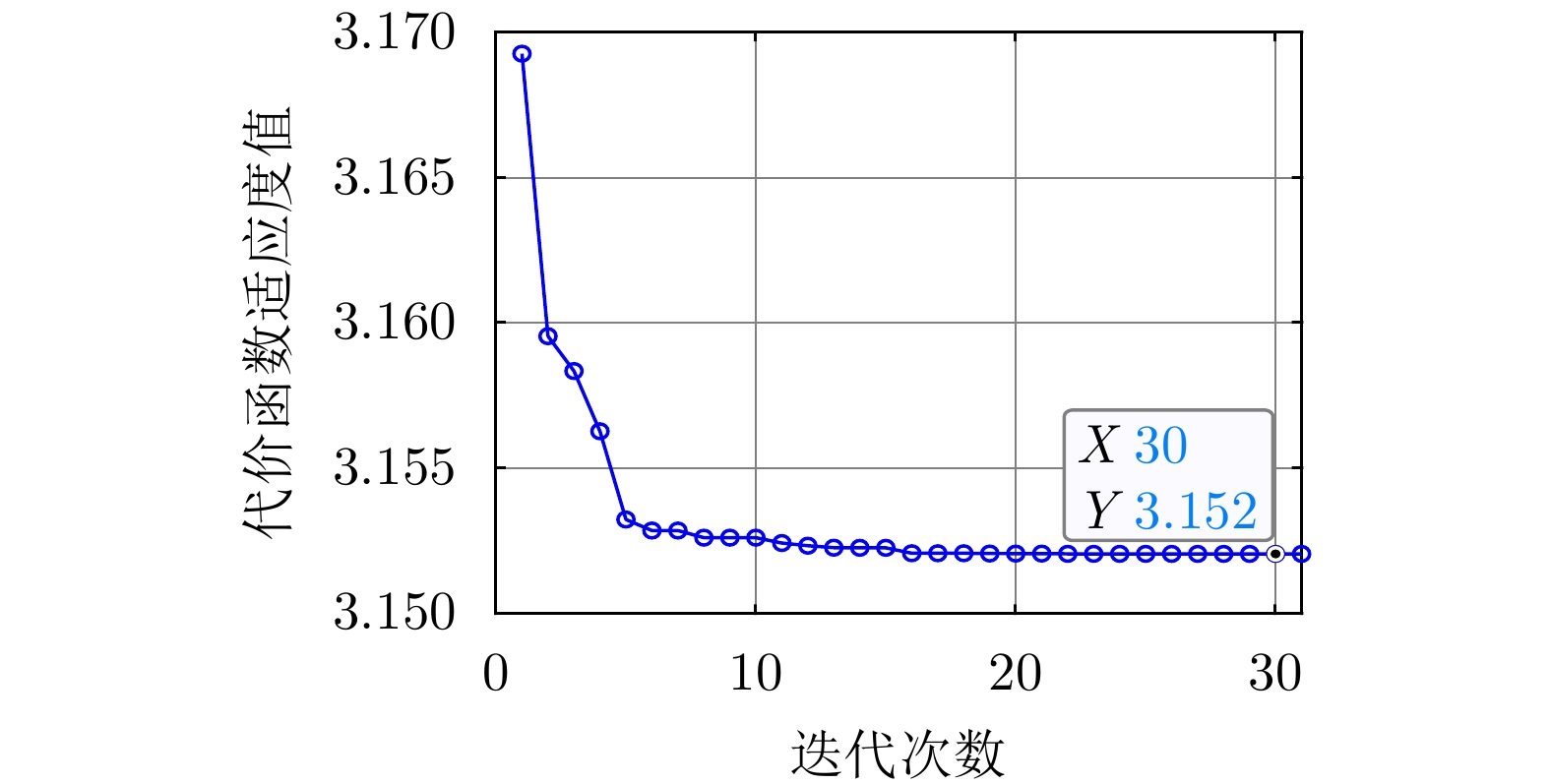
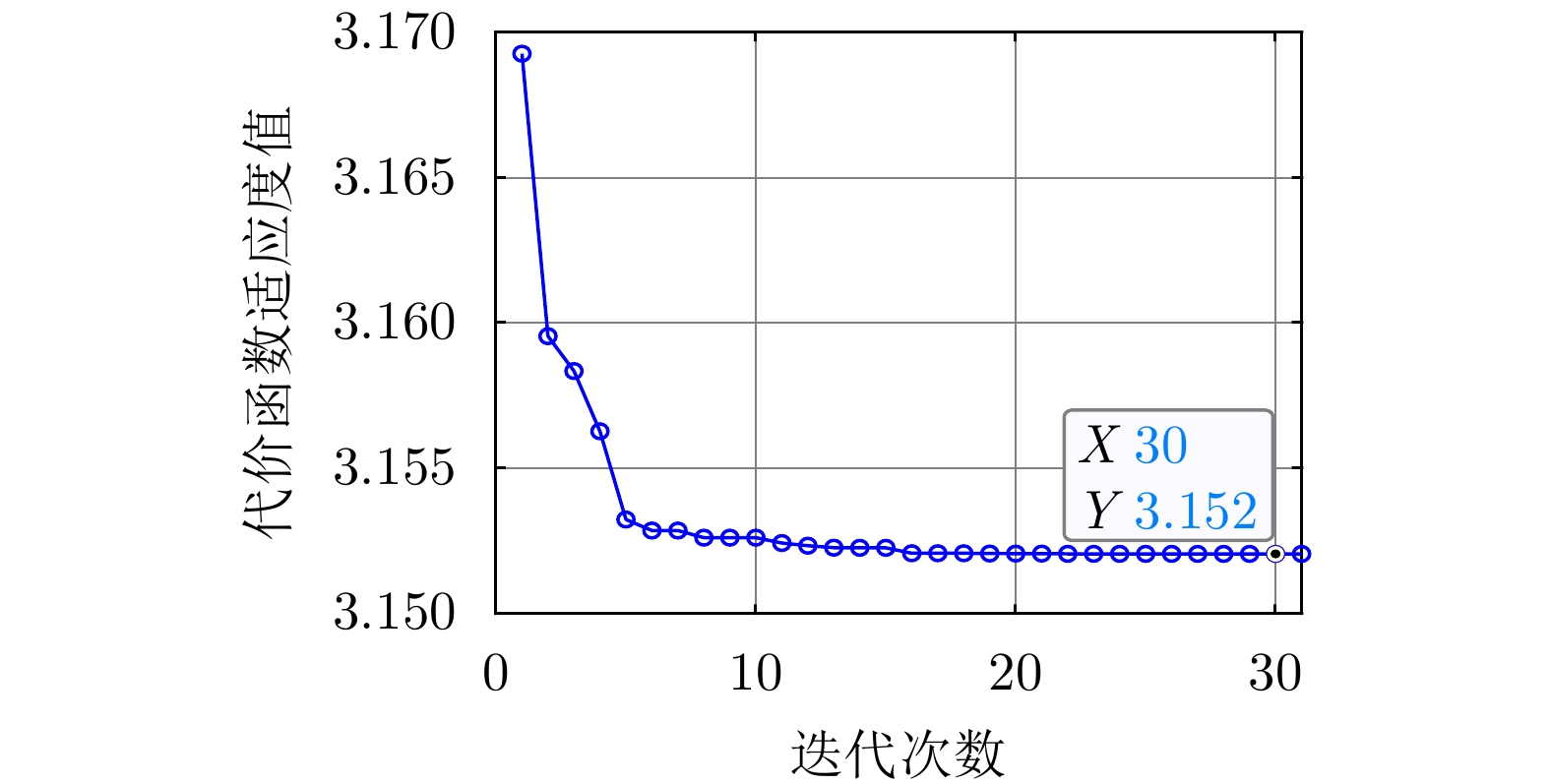
图9是用PSO求解优化问题式(33)时代价函数适应度值随迭代次数变化的曲线。由图9可见,随迭代次数增大,代价函数适应度值逐渐收敛,说明了PSO求解方法是可行的。
6. 结束语
本文针对多目标突防组网雷达的场景,提出了一种面向组网雷达干扰任务的多干扰机资源联合优化分配方法,在干扰资源有限的条件下,通过优化分配各干扰机的波束和功率资源,最小化组网雷达系统对突防目标的检测概率。之后,采用PSO分两步对上述优化问题进行求解。仿真结果表明,与传统方法相比,本文所提优化方法在干扰资源有限的条件下,通过优化配置干扰资源更能有效降低组网雷达对突防目标的检测概率,提升了多干扰机对组网雷达的协同压制干扰性能。需要指出的是,优化算法中的检测概率是在已知敌方组网雷达位置、融合方式以及融合准则等参数信息的理想情况下计算得到的。但在实际对抗环境中,考虑到获取组网雷达参数难度大和参数估计精度有限带来的检测概率泛化误差,本文建立了基于组网雷达参数不确定性的干扰资源稳健优化分配模型。仿真结果表明,相比传统方法,本文所提稳健方法提升了多干扰机对组网雷达的协同干扰性能,且有较好的鲁棒性。
-
表 1 不同融合准则下的组网雷达检测概率
Table 1. The detection probability of the NRS with different fusion rules
融合准则 检测概率 AND准则(K = N) {\rm{Pd} }_k^q = {\displaystyle\prod\limits_{i = 1}^N } {\rm{Pd} }_{i,k}^q OR准则(K = 1) {\rm{Pd} }_k^q = 1 - \displaystyle\prod \limits^N_{i = 1} (1 - {\rm{Pd} }_{i,k}^q) 秩K准则 {\rm{Pd} }_k^q = \displaystyle\sum\limits_{j = K}^N {\left\{ {\sum\limits_{\forall \left\{ {\sum {v_{i,k}^q = j} } \right\} } {\mathop \prod \limits_i { {({\rm{Pd} }_{i,k}^q)}^{v_{i,k}^q} }{ {(1 - {\rm{Pd} }_{i,k}^q)}^{1 - v_{i,k}^q} } } } \right\} } 表 2 基于PSO的波束指向
\boldsymbol{u}_k^{{\rm{opt}}} 求解方法Table 2. The solution algorithm of the beam selection
\boldsymbol{u}_k^{{\rm{opt}}} based on PSO步骤1 初始化\boldsymbol{P}_k^{{\rm{uni}}}, \boldsymbol{u}_k^{{\rm{opt}}}{\rm{ = }}{{\bf{0}}_{M \times N}}, \boldsymbol{u}_k^{{\rm{con}}} \in [0,1]; 步骤2 PSO求解式(32),得到松弛结果\boldsymbol{u}_{k,{\rm{opt}}}^{{\rm{con}}}; 步骤3 循环l = 1, 2,··· ,L \times M
寻找最大值[{m_l},{i_l}] = \arg \;\max \{ \boldsymbol{u}_{k,{\rm{opt}}}^{{\rm{con}}}\} ;
更新\boldsymbol{u}_k^{{\rm{opt}}}({m_l},{i_l}) = 1,且\boldsymbol{u}_{k,{\rm{opt}}}^{{\rm{con}}}({m_l},{i_l}) = 0;
判断\boldsymbol{u}_k^{{\rm{opt}}}是否满足式(2)—式(4)的约束条件,若不满足则
\boldsymbol{u}_k^{{\rm{opt}}}({m_l},{i_l}) = 0;
循环结束步骤4 输出波束指向结果\boldsymbol{u}_k^{{\rm{opt}}}。 表 3 干扰机工作参数
Table 3. The working parameters of the jammer
参数 数值 干扰机总功率P_m^{{\rm{total}}} 130 W 波束个数L 2 天线增益G_m^{\rm{J}} 10 dB 极化失配损失{\gamma ^{\rm{J}}} 0.5 工作波长{\lambda _{\rm{f}}} 0.1 m 天线波瓣宽度{\theta _{0.5}} 3° 表 4 雷达工作参数
Table 4. The working parameters of the radar node
参数 数值 发射功率P_i^{\rm{t}} 200 MW 最多被干扰波束个数S 1 发射天线增益G_i^{\rm{t}} 40 dB 虚警概率 10–6 工作波长{\lambda _{\rm{f}}} 0.1 m -
[1] 张养瑞, 高梅国, 罗皓月, 等. 基于检测概率的雷达网协同干扰效果评估方法[J]. 系统工程与电子技术, 2015, 37(8): 1778–1786. doi: 10.3969/j.issn.1001-506X.2015.08.10ZHANG Yangrui, GAO Meiguo, LUO Haoyue, et al. Evaluation method of cooperative jamming effect on radar net based on detection probability[J]. Systems Engineering and Electronics, 2015, 37(8): 1778–1786. doi: 10.3969/j.issn.1001-506X.2015.08.10 [2] ZHENG Gaoqian and ZHENG Ying. Radar netting technology & its development[C]. 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011: 933–937. doi: 10.1109/CIE-Radar.2011.6159694. [3] 时晨光, 汪飞, 周建江, 等. 基于低截获概率优化的雷达组网系统最优功率分配算法[J]. 雷达学报, 2014, 3(4): 465–473. doi: 10.3724/SP.J.1300.2014.13140SHI Chenguang, WANG Fei, ZHOU Jianjiang, et al. Optimal power allocation algorithm for radar network systems based on low probability of intercept optimization[J]. Journal of Radars, 2014, 3(4): 465–473. doi: 10.3724/SP.J.1300.2014.13140 [4] MA Jianming, LIU Yintong, and CHEN Guang. New jamming method of netted radar based on time synchronization errors[C]. 2019 International Conference on Information Technology, Electrical and Electronic Engineering, Sanya, China, 2019: 452–456. doi: 10.12783/dtcse/iteee2019/28787. [5] 段先华, 孙庆国, 蔡丹. 基于改进遗传算法的协同干扰资源优化分配[J]. 江苏科技大学学报: 自然科学版, 2016, 30(5): 466–472. doi: 10.3969/j.issn.1673-4807.2016.05.011DUAN Xianhua, SUN Qingguo, and CAI Dan. Optimization assignment for cooperative jamming resources based on improved genetic algorithms[J]. Journal of Jiangsu University of Science and Technology:Natural Science Edition, 2016, 30(5): 466–472. doi: 10.3969/j.issn.1673-4807.2016.05.011 [6] 张养瑞, 李云杰, 高梅国. 协同干扰资源优化分配模型及算法[J]. 系统工程与电子技术, 2014, 36(9): 1744–1749. doi: 10.3969/j.issn.1001-506X.2014.09.12ZHANG Yangrui, LI Yunjie, and GAO Meiguo. Optimal assignment model and solution of cooperative jamming resources[J]. Systems Engineering and Electronics, 2014, 36(9): 1744–1749. doi: 10.3969/j.issn.1001-506X.2014.09.12 [7] 黄郡, 单洪, 沈楠. 协同干扰节点资源优化分配模型及算法[J]. 计算机应用研究, 2011, 28(8): 2912–2914. doi: 10.3969/j.issn.1001-3695.2011.08.031HUANG Jun, SHAN Hong, and SHEN Nan. Optimal assignment model and solution of coordinated jamming nodes[J]. Application Research of Computers, 2011, 28(8): 2912–2914. doi: 10.3969/j.issn.1001-3695.2011.08.031 [8] 谯梁, 杨帅, 王鑫, 等. 雷达干扰效果评估与协同干扰策略分配算法研究[J]. 航天电子对抗, 2019, 35(3): 27–32. doi: 10.3969/j.issn.1673-2421.2019.03.007QIAO Liang, YANG Shuai, WANG Xin, et al. Effect evaluation of radar interference and cooperative interference strategy allocation algorithm[J]. Aerospace Electronic Warfare, 2019, 35(3): 27–32. doi: 10.3969/j.issn.1673-2421.2019.03.007 [9] 孙伯明, 梁修华, 吴付祥. 多波束雷达干扰机作战效能分析[J]. 舰船电子对抗, 2007, 30(5): 40–42. doi: 10.16426/j.cnki.jcdzdk.2007.05.025SUN Boming, LIANG Xiuhua, and WU Fuxiang. Operation effectiveness analysis of multi-beam radar jammer[J]. Shipboard Electronic Countermeasure, 2007, 30(5): 40–42. doi: 10.16426/j.cnki.jcdzdk.2007.05.025 [10] 韩剑, 张杰. 多波束及其在无人机上的应用[J]. 航天电子对抗, 2014, 30(2): 47–50. doi: 10.3969/j.issn.1673-2421.2014.02.014HAN Jian and ZHANG Jie. Multi-beam technology and applications to UAV[J]. Aerospace Electronic Warfare, 2014, 30(2): 47–50. doi: 10.3969/j.issn.1673-2421.2014.02.014 [11] 李光明, 田孝华, 刘潇, 等. 智能多波束干扰技术研究[J]. 电光与控制, 2017, 24(4): 1–4.LI Guangming, TIAN Xiaohua, LIU Xiao, et al. On multi-beam jamming technology based on array antenna[J]. Electronics Optics &Control, 2017, 24(4): 1–4. [12] LUO Zhaoyi, DENG Min, YAO Zhiqiang, et al. Distributed blanket jamming resource scheduling for satellite navigation based on particle swarm optimization and genetic algorithm[C]. The 2020 IEEE 20th International Conference on Communication Technology, Nanning, China, 2020: 611–616. doi: 10.1109/ICCT50939.2020.9295811. [13] 李昌锦, 陈永光, 沈阳, 等. 突防过程的组网雷达干扰资源优化分配[J]. 火力与指挥控制, 2006, 31(10): 8–10, 25. doi: 10.3969/j.issn.1002-0640.2006.10.003LI Changjin, CHEN Yongguang, SHEN Yang, et al. On study of optimum allocation for jamming resource against netted radar based on penetrating process[J]. Fire Control and Command Control, 2006, 31(10): 8–10, 25. doi: 10.3969/j.issn.1002-0640.2006.10.003 [14] 沈阳, 陈永光, 李修和. 基于0-1规划的雷达干扰资源优化分配研究[J]. 兵工学报, 2007, 28(5): 528–532. doi: 10.3321/j.issn:1000-1093.2007.05.005SHEN Yang, CHEN Yongguang, and LI Xiuhe. Research on optimal distribution of radar jamming resource based on zero-one programming[J]. Acta Armamentarii, 2007, 28(5): 528–532. doi: 10.3321/j.issn:1000-1093.2007.05.005 [15] 戴少怀, 杨革文, 李旻, 等. 改进粒子群算法的组网雷达协同干扰资源分配[J]. 航天电子对抗, 2020, 36(4): 29–34, 45. doi: 10.3969/j.issn.1673-2421.2020.04.007DAI Shaohuai, YANG Gewen, LI Min, et al. Cooperative jamming resources allocation of networked radar based on improved particle swarm optimization algorithm[J]. Aerospace Electronic Warfare, 2020, 36(4): 29–34, 45. doi: 10.3969/j.issn.1673-2421.2020.04.007 [16] 陈奕琪. 改进群智能算法多目标干扰决策[J]. 现代防御技术, 2020, 48(1): 107–112. doi: 10.3969/j.issn.1009-086x.2020.01.017CHEN Yiqi. Improved swarm intelligence algorithm for multi-objective jamming decision[J]. Modern Defence Technology, 2020, 48(1): 107–112. doi: 10.3969/j.issn.1009-086x.2020.01.017 [17] 郭小一, 袁卫卫, 黄金才. 雷达干扰资源一对多分配方法[J]. 火力与指挥控制, 2008, 33(12): 22–25, 29. doi: 10.3969/j.issn.1002-0640.2008.12.006GUO Xiaoyi, YUAN Weiwei, and HUANG Jincai. Research on method of radar jamming resource distribution based on one-jammer to multi-radar[J]. Fire Control and Command Control, 2008, 33(12): 22–25, 29. doi: 10.3969/j.issn.1002-0640.2008.12.006 [18] 高晓光, 胡明, 郑景嵩. 突防任务中的单机对多目标干扰决策[J]. 系统工程与电子技术, 2010, 32(6): 1239–1243. doi: 10.3969/j.issn.1001-506X.2010.06.028GAO Xiaoguang, HU Ming, and ZHENG Jingsong. Jamming strategy for single plane to multi-target in task of penetration[J]. Systems Engineering and Electronics, 2010, 32(6): 1239–1243. doi: 10.3969/j.issn.1001-506X.2010.06.028 [19] 崔哲铭, 彭世蕤, 任明秋, 等. 基于波束数量控制的多波束干扰资源调度研究[J]. 空军预警学院学报, 2020, 34(4): 274–278. doi: 10.3969/j.issn.2095-5839.2020.04.009CUI Zheming, PENG Shirui, REN Mingqiu, et al. Research on multi-beam interference resource scheduling based on beam quantity control[J]. Journal of Air Force Early Warning Academy, 2020, 34(4): 274–278. doi: 10.3969/j.issn.2095-5839.2020.04.009 [20] 张政超, 徐裴为, 李文臣, 等. 复杂电磁干扰下组网雷达检测概率研究[J]. 中国电子科学研究院学报, 2014, 9(4): 391–395. doi: 10.3969/j.issn.1673-5692.2014.04.013ZHANG Zhengchao, XU Peiwei, LI Wenchen, et al. Research on detected probability of radar network under complex electromagnetism jamming[J]. Journal of CAEIT, 2014, 9(4): 391–395. doi: 10.3969/j.issn.1673-5692.2014.04.013 [21] 王红军, 赵宏. 噪声干扰条件下雷达检测概率的评估[J]. 火力与指挥控制, 2003, 28(1): 40–42. doi: 10.3969/j.issn.1002-0640.2003.01.010WANG Hongjun and ZHAO Hong. Evalution of the radar detecting probability under noise jamming[J]. Fire Control & Command Control, 2003, 28(1): 40–42. doi: 10.3969/j.issn.1002-0640.2003.01.010 [22] 周怀军, 丁士援. 噪声干扰条件下雷达检测概率分析[J]. 舰船电子对抗, 2007, 30(6): 43–45. doi: 10.16426/j.cnki.jcdzdk.2007.06.007ZHOU Huaijun and DING Shiyuan. Analysis of radar detection probability under the noise jamming condition[J]. Shipboard Electronic Countermeasure, 2007, 30(6): 43–45. doi: 10.16426/j.cnki.jcdzdk.2007.06.007 [23] JIANG Haiqing, ZHANG Yangrui, and XU Hongyi. Optimal allocation of cooperative jamming resource based on hybrid quantum-behaved particle swarm optimisation and genetic algorithm[J]. IET Radar, Sonar & Navigation, 2017, 11(1): 185–192. doi: 10.1049/iet-rsn.2016.0119 [24] 胡新宇, 张铁军, 王昀. 低截获概率雷达信号侦察技术[J]. 航天电子对抗, 2020, 36(5): 40–43. doi: 10.16328/j.htdz8511.2020.05.009HU Xinyu, ZHANG Tiejun, and WANG Yun. Low probability of intercept radar signal reconnaissance technology[J]. Aerospace Electronic Warfare, 2020, 36(5): 40–43. doi: 10.16328/j.htdz8511.2020.05.009 [25] MA Jing, SHI Bin, CHE Fei, et al. Research on evaluation method of cooperative jamming effect in cognitive confrontation[C]. The 1st International Conference on Artificial Intelligence for Communications and Networks, Harbin, China, 2019: 40–51. [26] ZHANG Lin, SHI Guoqing, and GENG Xiutang. Blanket jamming targets assignment based on adaptive genetic algorithm[C]. 2019 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Bangkok, Thailand, 2019: 171–175. doi: 10.1109/CIS-RAM47153.2019.9095841. [27] SHEN Tongyun, DING Jianjiang, DING Yuan, et al. A method of detection performance modeling in jamming condition based on radar network system[C]. 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011: 1366–1369. doi: 10.1109/CIE-Radar.2011.6159812. [28] ZHANG Huan, YANG Rennong, SUN Changyue, et al. Research on multiaircraft cooperative suppression interference array based on an improved multiobjective particle swarm optimization algorithm[J]. Mathematical Problems in Engineering, 2017, 2017: 9843735. doi: 10.1155/2017/9843735 [29] 马哈夫扎, 挨尔舍贝利, 朱国富, 黄晓涛, 黎向阳, 等译. 雷达系统设计MATLAB仿真[M]. 北京: 电子工业出版社, 2009.MAHAFZA B R, ELSHERBENI A Z, ZHU Guofu, HUANG Xiaotao, LI Xiangyang, et al. translation. MATLAB Simulations for Radar Systems Design[M]. Beijing: Publishing House of Electronics Industry, 2009. [30] LIU Weijian, WANG Yongliang, LIU Jun, et al. Performance analysis of adaptive detectors for point targets in subspace interference and gaussian noise[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 429–441. doi: 10.1109/TAES.2017.2760718 [31] 韩国玺, 何俊, 祁建清. 基于秩K准则的网络雷达对抗系统融合发现概率计算模型[J]. 海军工程大学学报, 2014, 26(1): 64–70.HAN Guoxi, HE Jun, and QI Jianqing. Fused detection probability model of NRCS based on rank K criterion[J]. Journal of Naval University of Engineering, 2014, 26(1): 64–70. [32] 王国良, 申绪涧, 汪连栋, 等. 基于秩K融合规则的组网雷达系统干扰效果评估[J]. 系统仿真学报, 2009, 21(23): 7678–7680.WANG Guoliang, SHEN Xujian, WANG Liandong, et al. Effect evaluation for noise blanket jamming against netted radars based on rank-K information fusion rules[J]. Journal of System Simulation, 2009, 21(23): 7678–7680. [33] YI Wei, YUAN Ye, HOSEINNEZHAD R, et al. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2020, 68: 1602–1617. doi: 10.1109/TSP.2020.2976587 [34] YAN Junkun, LIU Hongwei, JIU Bo, et al. Simultaneous multibeam resource allocation scheme for multiple target tracking[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3110–3122. doi: 10.1109/TSP.2015.2417504 [35] YAN Junkun, LIU Hongwei, PU Wenqiang, et al. Joint beam selection and power allocation for multiple target tracking in netted colocated MIMO radar system[J]. IEEE Transactions on Signal Processing, 2016, 64(24): 6417–6427. doi: 10.1109/TSP.2016.2607147 期刊类型引用(14)
1. 阎潇,王青平,胡卫东,朱虹宇,王超. 基于椋鸟迁徙的干扰资源动态分配方法. 系统工程与电子技术. 2025(05): 1385-1394 .  百度学术
百度学术2. 胡继军,韩伟,张国玉,周希娃,贺杨婷,廖春兰. 基于多站数据融合的参数精估计方法. 遥测遥控. 2024(02): 109-123 .  百度学术
百度学术3. 赵宏宇,武忠国,李廷鹏,杨晓帆,陈冬冬. 射频信号合成与数字域信号合成的等效性分析. 电子信息对抗技术. 2024(03): 21-26 .  百度学术
百度学术4. 廖晓容,孙国皓,钟苏川,余显祥,李明. 面向多任务动态场景的雷达与干扰空时协同波束联合优化方法. 雷达学报. 2024(03): 613-628 .  本站查看
本站查看5. 邹玮琦,牛朝阳,刘伟,王艳云,湛嘉祺. 面向组网雷达干扰任务的多机伴随式编队航迹预规划方法. 系统工程与电子技术. 2024(08): 2807-2819 .  百度学术
百度学术6. 刘溥熙,赵欣怡,尤明,田栢苓,马龙. 面向组网雷达干扰任务的多无人机协同动态决策方法研究. 战术导弹技术. 2024(06): 14-25 .  百度学术
百度学术7. 袁野,杨剑,刘辛雨,易伟,孔令讲. 基于任务效用最大化的多雷达协同任务规划算法. 雷达学报. 2023(03): 550-562 .  本站查看
本站查看8. 王跃东,顾以静,梁彦,王增福,张会霞. 伴随压制干扰与组网雷达功率分配的深度博弈研究. 雷达学报. 2023(03): 642-656 .  本站查看
本站查看9. 时晨光,董璟,周建江. 频谱共存下面向多目标跟踪的组网雷达功率时间联合优化算法. 雷达学报. 2023(03): 590-601 .  本站查看
本站查看10. 齐铖,谢军伟,张浩为,丁梓航,杨潇. 基于目标检测的混合分布式PA-MIMO雷达系统阵元优化部署. 雷达学报. 2023(03): 576-589 .  本站查看
本站查看11. 纪慧颖,潘明海,张元时,喻庆豪. 基于遗传-蚁群融合算法的干扰资源分配方法. 系统工程与电子技术. 2023(07): 2098-2107 .  百度学术
百度学术12. 陆德江,王星,陈游,胡星. 联合多种资源协同干扰组网雷达系统的自适应调度方法. 系统工程与电子技术. 2023(09): 2744-2754 .  百度学术
百度学术13. 梁猛,檀雷,陈飞,梁斌,杨帅. 协同干扰技术应用研究. 航天电子对抗. 2023(04): 44-48+64 .  百度学术
百度学术14. 李健涛,王轲昕,刘凯,张天贤. 基于深度强化学习的干扰资源分配方法. 现代雷达. 2023(10): 44-51 .  百度学术
百度学术其他类型引用(14)
-



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公

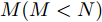
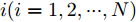
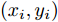
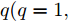
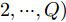
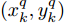
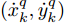
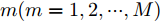
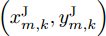

 下载:
下载:

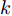
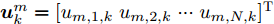
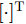
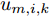
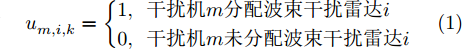

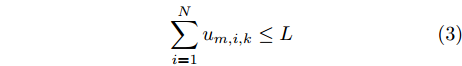
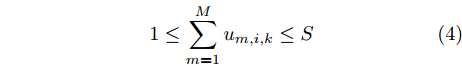
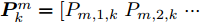
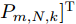
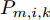
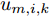

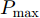
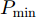
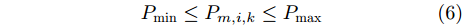
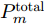
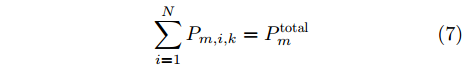
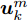
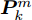
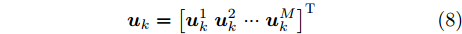
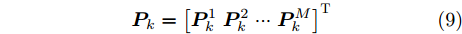

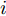
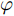
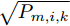
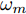
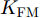
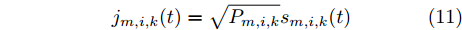
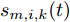


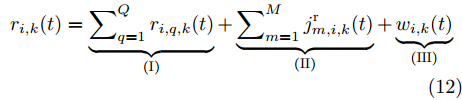

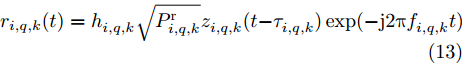
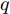
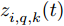
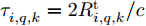
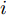
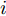
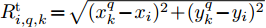
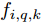
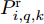
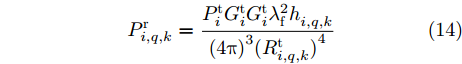
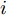
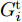
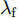
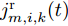
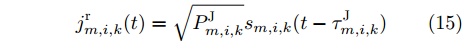
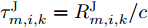


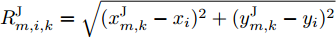
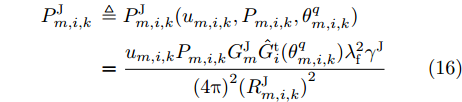
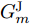


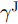
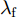
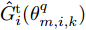
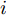
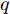
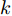

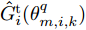
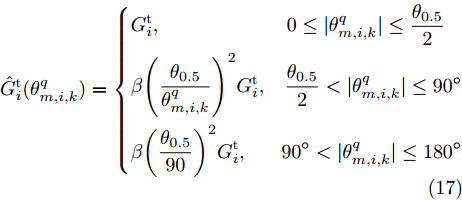
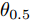
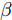
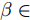
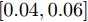
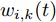
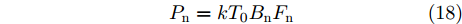
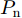
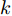
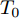
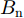
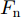
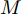
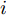
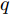
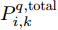
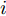
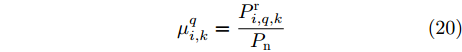
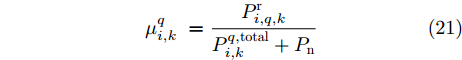
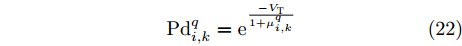
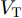
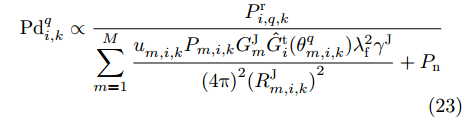
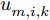
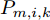
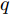
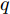
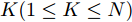
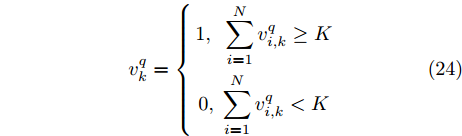
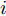
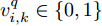
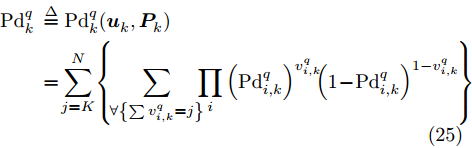
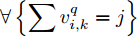
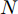
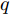
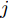

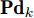
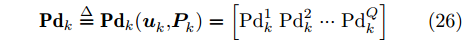
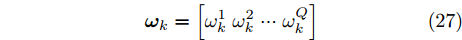
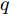
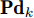
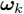
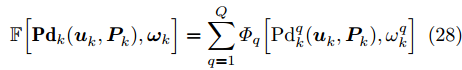
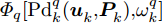
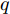
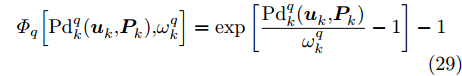
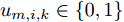
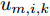
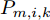
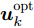
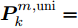
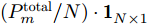
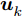
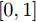
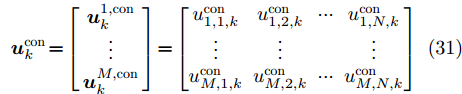
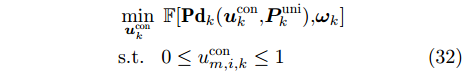
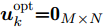
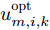
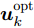
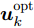
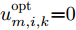
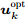
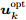
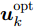
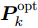
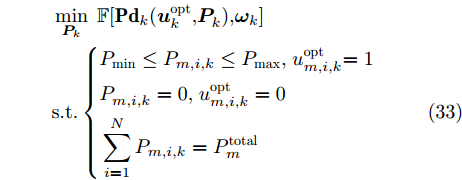
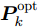
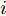

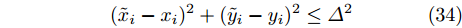
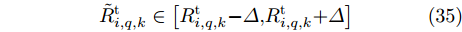
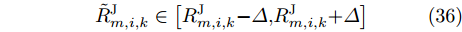
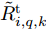
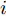
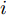
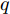
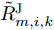

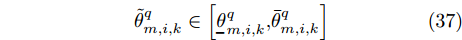
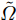
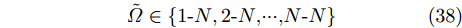
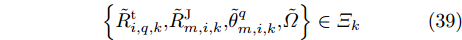
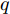
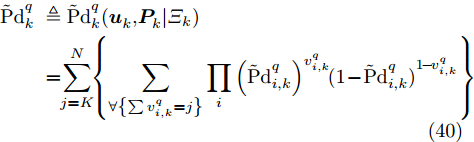
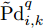
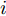
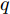
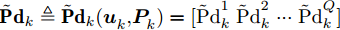
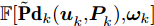
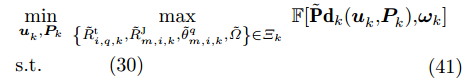
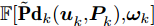
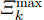
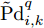
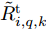
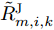
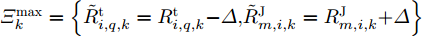
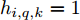
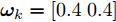
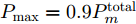
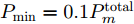
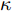
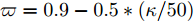



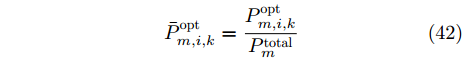
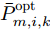

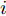





 下载:
下载:




 百度学术
百度学术