-
摘要: 通过在超表面单元上加载二极管等有源器件,可编程超表面可实现对电磁波的实时灵活调控。通常利用全波仿真软件计算可编程超表面的辐射场,但该方法需要消耗大量的时间,因而降低了设计效率。为了实现准确高效求解给定编码序列计算辐射场,该文首先设计了辐射场自动测试系统,利用该测试系统实测了少量的编码和辐射场数据,其后提出了一个正向深度神经网络,基于实测的数据训练该神经网络,最终实现了给定编码准确高效预测辐射场。对于给定辐射场求解编码的逆问题,该文提出了一个逆向深度神经网络。基于正向网络生成的数据训练所提出的逆向网络,最终实现了给定辐射场实时准确求解编码。该文所提出的方法为雷达波束形成提供了一种新可选方案,在雷达智能波束形成、微波成像等领域有一定的应用价值。Abstract: The Programmable Metasurface (PM) can flexibly manipulate electromagnetic waves in real time using loading active devices on the meta-element. Calculating the radiation fields of the PM with complex structures using full-wave simulation software is time-consuming, which results in design efficiency. To accurately and efficiently solve the mapping relationship from coding schemes to radiation fields, an Auto-Measuring System (AMS) of radiation patterns is designed. A few Code-to-Pattern (C-P) data are measured via the AMS. Then, a forward Deep Neural Network (DNN) is proposed, the DNN is trained by the measured data, and an accurate and efficient prediction of C-P is realized. More C-P data are generated based on the proposed forward neural network, and the data are used to train another proposed inverse DNN and realize the accurate prediction of codes when given patterns in real time. This method provides a new alternative scheme for radar beamforming and has application values in intelligent radar beamforming and microwave imaging.
-
1. 引 言
电磁超材料是由亚波长单元按一定规律组成的人工结构,具备自然界中材料不存在的特殊电磁特性。电磁超材料最早由苏联科学家Veselago等人[1]于1968年提出,由于当时实验条件所限,对超材料的研究停留在理论阶段。1996年帝国理工学院Pendry等人[2]利用周期性金属结构在实验上首次实现了等效负介电常数,继而引起越来越多学者的关注。数字编码超材料将相位相差180°的两种超材料单元作为数字单元0和1,通过改变数字编码序列即可实现对电磁波的调控[3]。可编程超表面是通过在二维数字编码超材料单元上加载二极管等,利用现场可编程门阵列(Field Programmable Gate Array, FPGA)控制二极管的导通和断开来实现多功能实时调控电磁波[4]。对于电尺寸较大结构复杂的可编程超表面,利用全波仿真软件计算多个编码序列对应的辐射场时,需要消耗大量时间,极大地降低了可编程超表面的设计效率。
深度学习技术通过计算多层神经网络将初始的“低层”特征表示转化为“高层”特征表示,可从大量的数据中“学习”其内在的物理规律。目前已经在语音识别[5-6]、图像处理[7]等领域得到了广泛的应用。由于可编程超表面存在大量不同编码对应的不同辐射场,提供了深度学习训练所需的数据,因而利用深度学习算法预测可编程超表面不同编码对应的辐射场成为可能。随着深度学习算法的不断完善,硬件算力的不断提升,深度学习在求解电大尺寸复杂结构可编程超表面编码序列与辐射场映射关系上有独特的优势。
本文针对给定编码序列高效准确求解可编程超表面辐射场的问题,首先设计了一套辐射场自动测试系统,动态切换编码并同时高效测量其辐射场。基于测量的少量编码-方向图数据训练提出的正向深度神经网络,最终实现了给定编码准确高效预测其对应的辐射场。利用该正向网络可以生成更多的辐射场数据,基于生成的数据和实测数据训练逆向深度神经网络,实现了实时准确求解给定辐射场逆向求解其对应编码。本文的创新性在于:(1)采用少量实测数据训练神经网络,实现对于整个编码空间的方向图预测,大大减少方向图计算量。(2)首先采用正向映射的深度神经网络产生更多方向图数据来训练从方向图求编码的逆向映射网络,其次提出了一个深度神经网络实现了从方向图到编码的逆向计算。基于所提出可编程超表面,提供了一个完整的同时包括正向和逆向计算的智能波束形成方案。
本文第2节给出可编程超表面结构和辐射场自动测试系统,第3节详细描述正向映射网络及其预测结果,第4节给出逆向映射网络及其预测结果,第5节对全文总结概括。
2. 可编程超表面设计与自动测试系统
2.1 可编程超表面设计
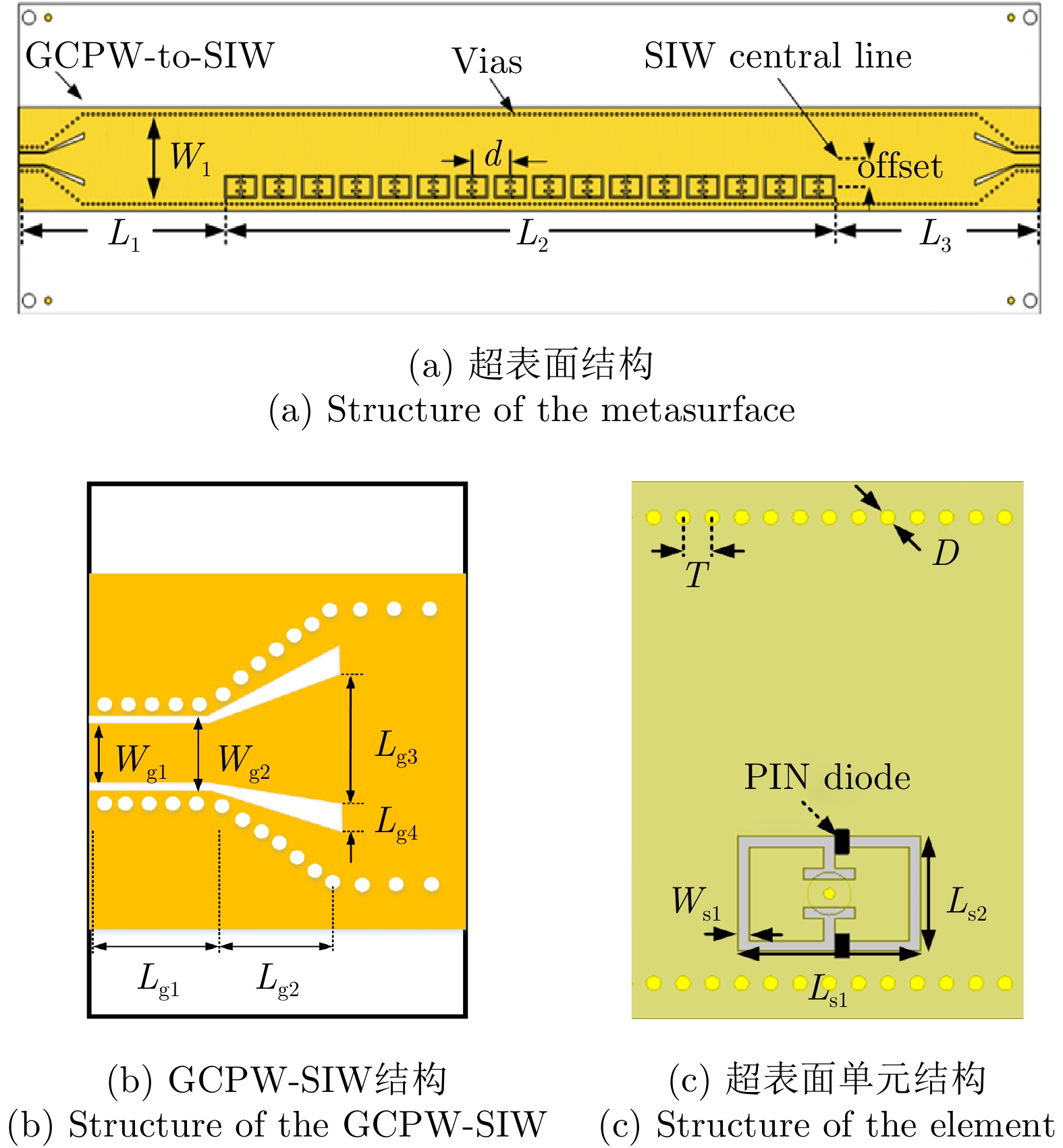
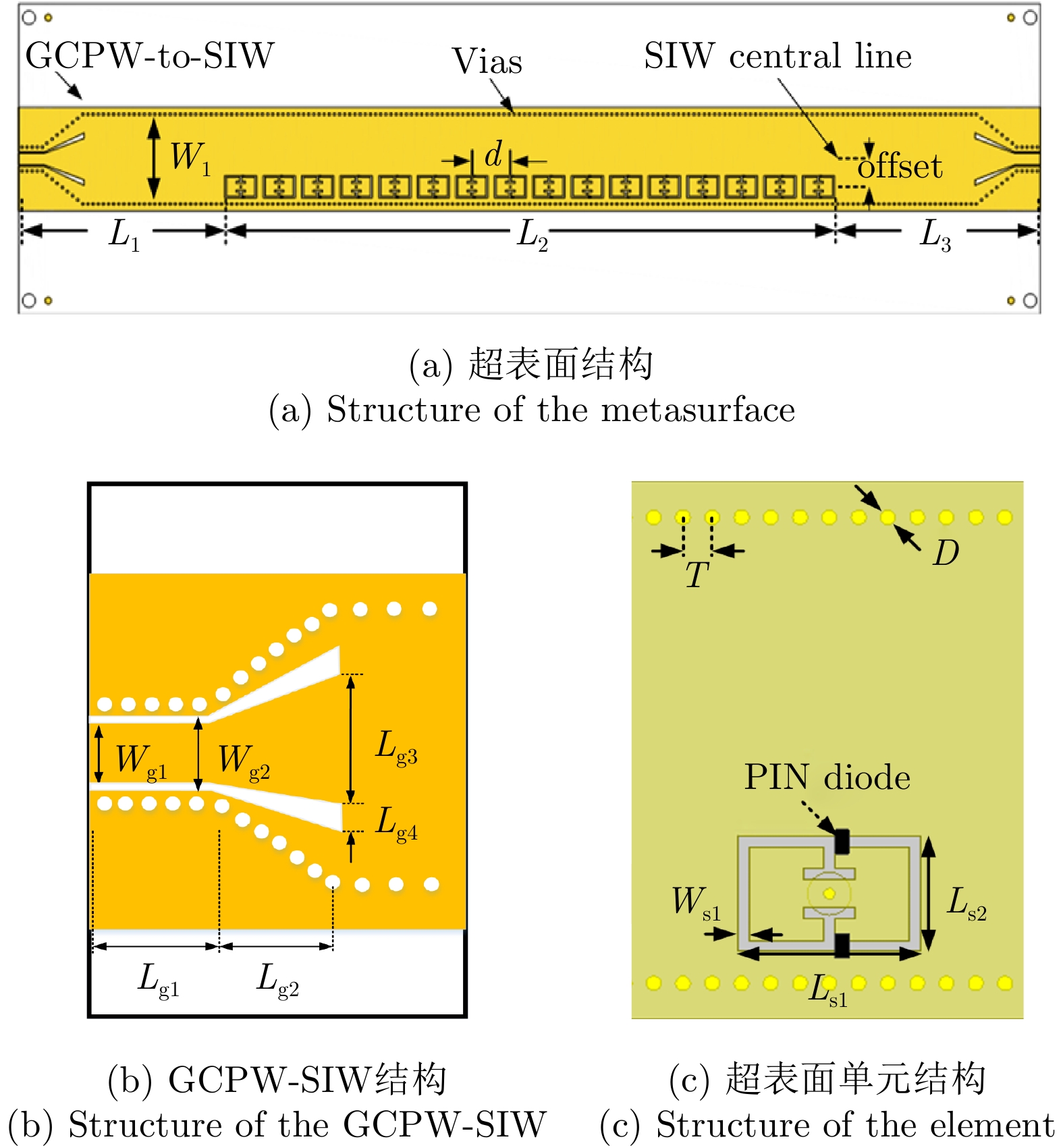
本文所提出的可编程超表面结构基于文献[4]中提出的结构,超表面结构如图1(a)所示,超表面包含16个单元,单元间距为6 mm。超表面采用侧馈的方式,接地共面波导(Grounded Coplanar Waveguide, GCW)转基片集成波导(Substrate Integrate Waveguide, SIW)的馈电结构可以在保证较好阻抗匹配的同时降低寄生辐射,GCPW-SIW结构如图1(b)所示。超表面单元为在基片集成波导上表面刻蚀互补电容电感谐振器(cELC)单元,如图1(c)所示,单元包含3层金属结构和3层介质。最上层为厚度1.524 mm的罗杰斯4003介质,中间层为厚度0.101 mm的Ro4450粘接层,底层为厚度0.508 mm的罗杰斯4003介质。在cELC单元的容性缝隙之间加载了两个二极管(MADP-000907-14020W),利用现场可编程门阵列控制二极管的通断,从而实现超表面单元在辐射态和非辐射态之间动态切换。二极管导通时可等效为电感L1=0.1 nH和电阻R1=5 Ω的串联,断开时可等效为电感L2=0.1 nH和电容C1=0.025 pF的串联。超表面各相关参数如表1所示。cELC最外层的矩形缝隙可等效为电容,电流经过cELC单元内部“T”字缝隙的时候,会形成环状电流,该环状电流可等效为电感效应。通过合理的设计外层矩形缝隙的尺寸和“T”字缝隙的长宽,可使得cELC单元在目标频率处获得较好的谐振性能。
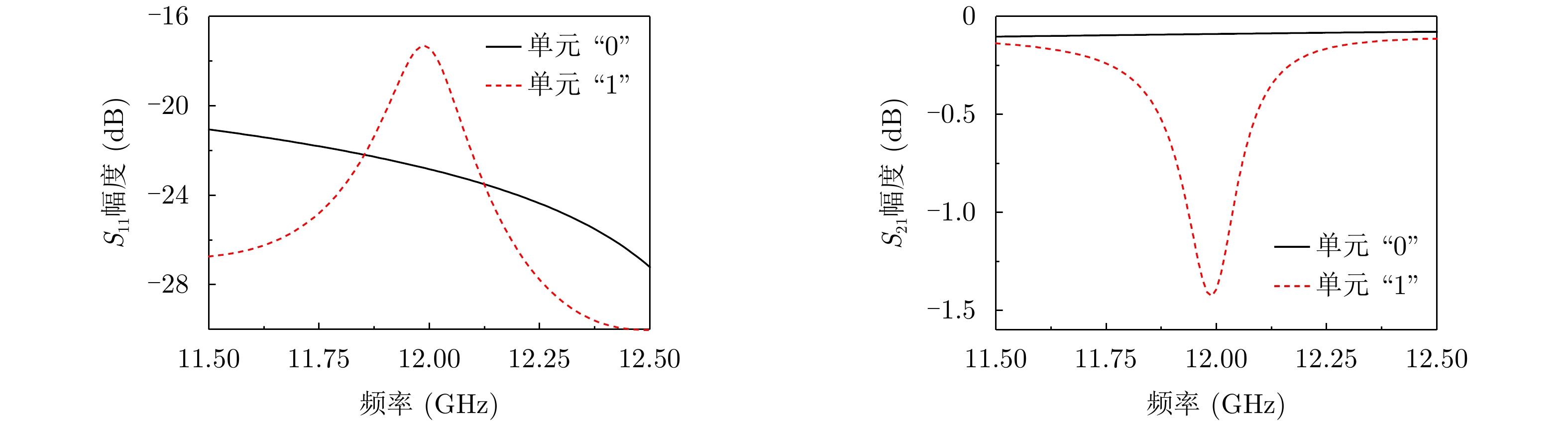
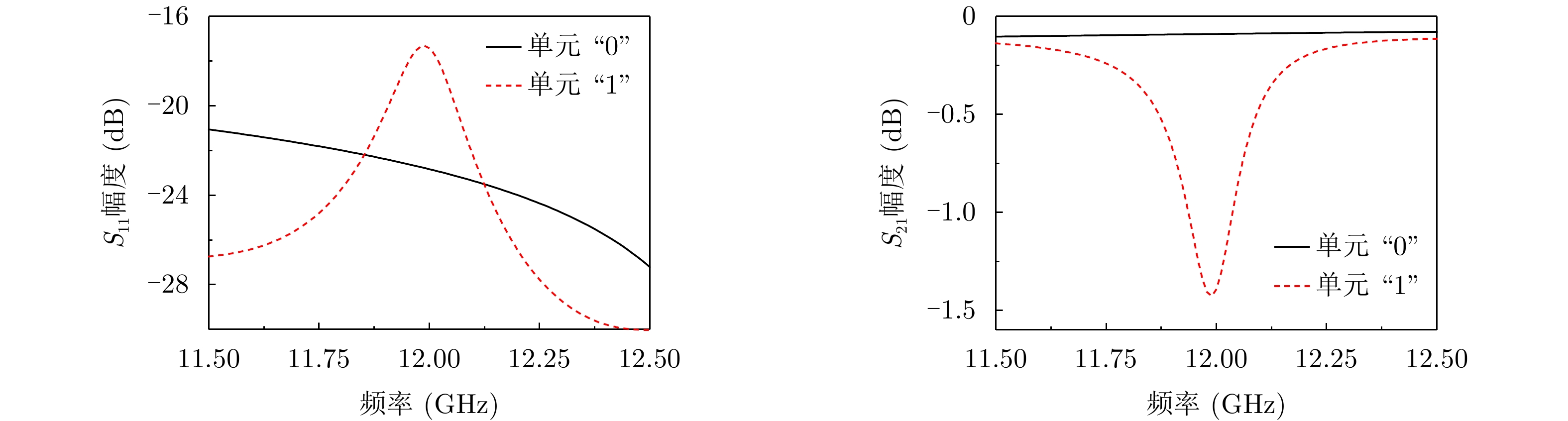
表 1 超表面相关参数(mm)Table 1. Parameters of the metasurface (mm)L1 L2 L3 W1 offset d Wfeed Lg1 Lg2 Lg3 32.1 95 32.1 13 4 6 1.65 3.7 6.3 6 Lg4 Wg1 Wg2 Ls1 Ls2 Ws1 T D h1 h2 0.8 1.65 2.05 5 3.2 0.3 0.8 0.4 1.524 0.508 利用全波仿真软件HFSS优化分析所设计的超表面单元。单元的端口1和端口2均设置为去嵌入端口且为TE10模激励。把二极管导通时记为单元“0”,二极管断开时记为单元“1”,仿真单元散射参数结果如图2所示[4]。在频率11.5 GHz到12.5 GHz频段,单元S11均小于–15 dB。二极管断开时单元“1”在12 GHz处谐振,S21=–1.42 dB,此时小部分能量被耦合到自由空间中形成辐射。单元“1”的谐振点随着T形缝隙的尺寸和内外金属导体缝隙的尺寸而改变。二极管导通时,谐振点消失,12 GHz处S21=–0.089 dB,大部分能量从1端口传输到2端口。由于cELC偏离SIW中心放置,单元的状态对导行波的相位影响较小。通过控制二极管的通断可以实现超表面单元在辐射态和非辐射态之间动态切换。
端口1设置为激励端口,端口2为匹配端口吸收余下的导行波。导行波从端口1沿着SIW传播时,依次激励SIW上表面加载的超表面单元,不同单元位置处的激励相位不同。超表面实现波束电扫描的物理机理为:当导行波沿SIW传播并激励cELC单元时,由于导行波的相位积累,不同编码序列下处于辐射态单元之间的相位差不同,由相控阵天线原理可知,不同单元间相位差对应主瓣指向不同,从而使超表面产生了不同指向的方向图。
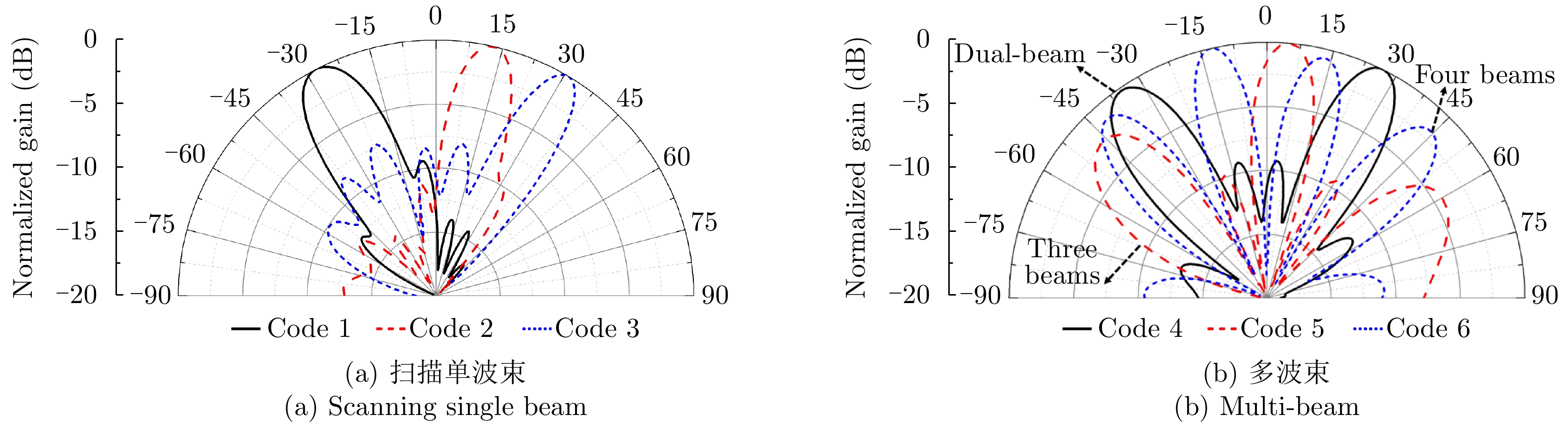
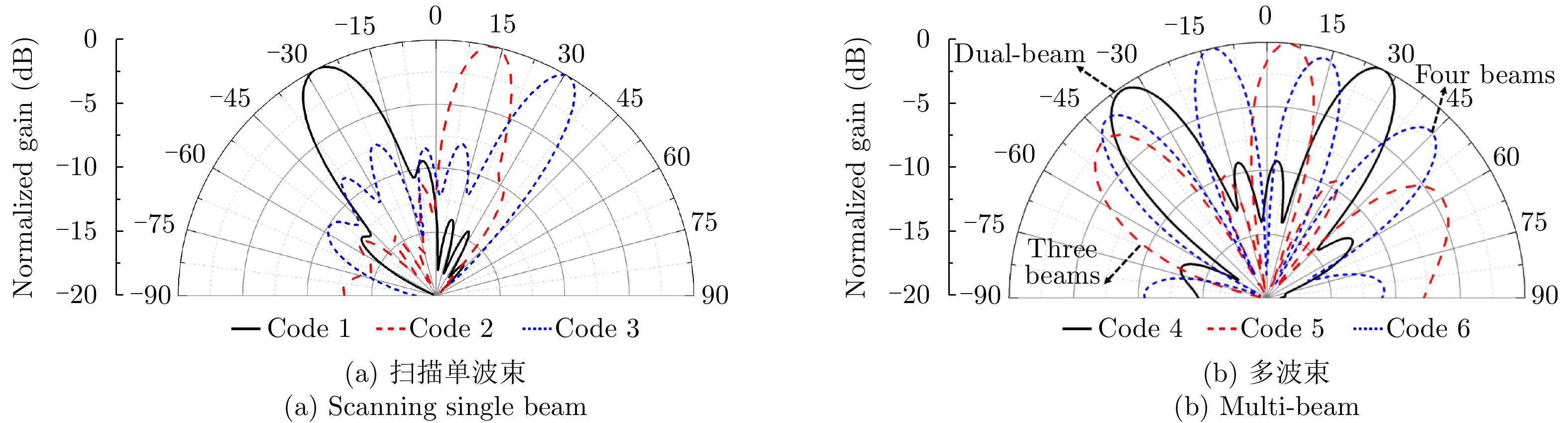
表2和表3分别展示了不同编码序列下,所提出超表面产生的扫描波束和多波束。图3(a)为表格1所示编码对应的扫描波束,当分别输入编码1、编码2和编码3时,超表面产生指向分别为–25°, 14°和32°的单波束,3 dB波束宽度分别为13.0°, 13.0°,和8.5°。如图3(b)所示,当分别输入表格2中编码4、编码5、编码6时,超表面分别产生双波束、三波束和四波束。超表面还可以产生更多的扫描波束和复杂波束,此处仅给出6个编码作为示例。
表 2 单波束编码Table 2. Codes for single beams编码号 编码序列 主瓣指向 波束宽度 Code 1 0101010101010101 –28° 13.5° Code 2 1001001001001001 13° 10.0° Code 3 1001100110011001 31° 8.5° 表 3 多波束编码Table 3. Codes for multi-beam编码号 编码序列 波束个数 Code 4 0001000100010001 2 Code 5 0000100001000010 3 Code 6 0000010000010000 4 2.2 自动测试系统
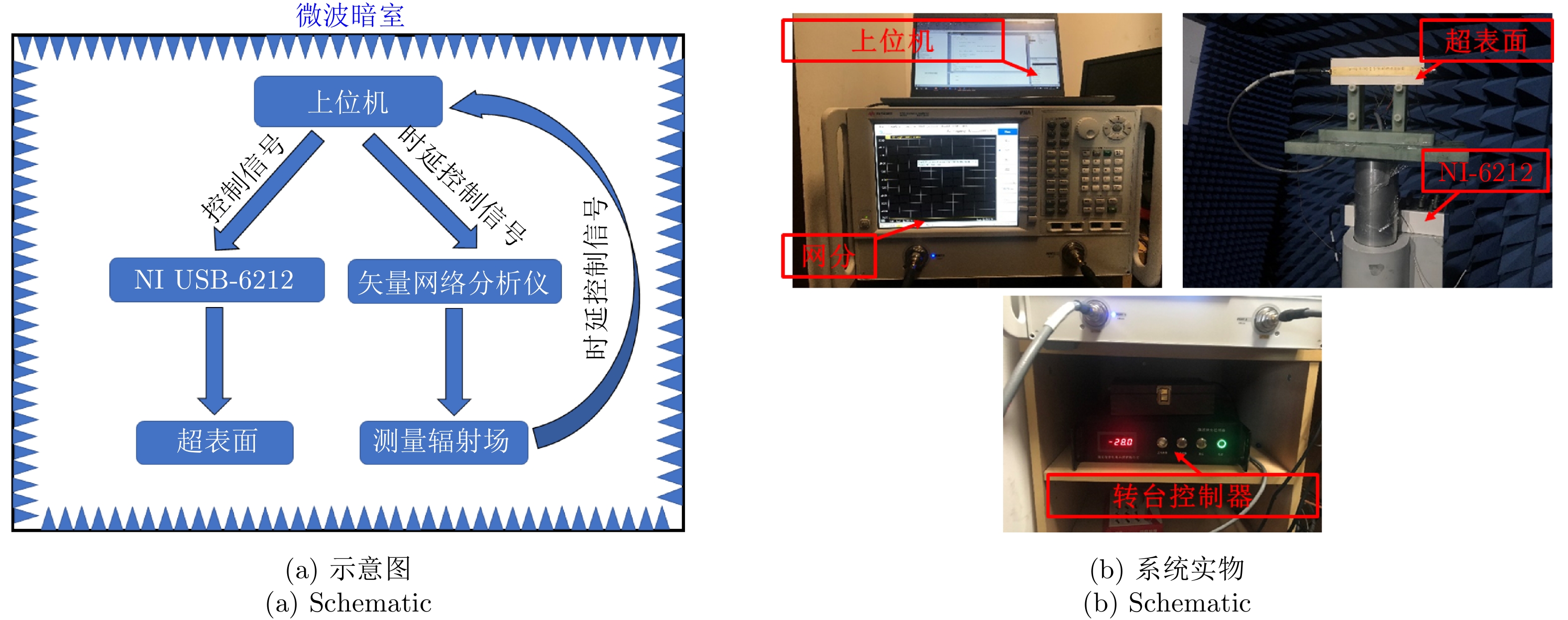
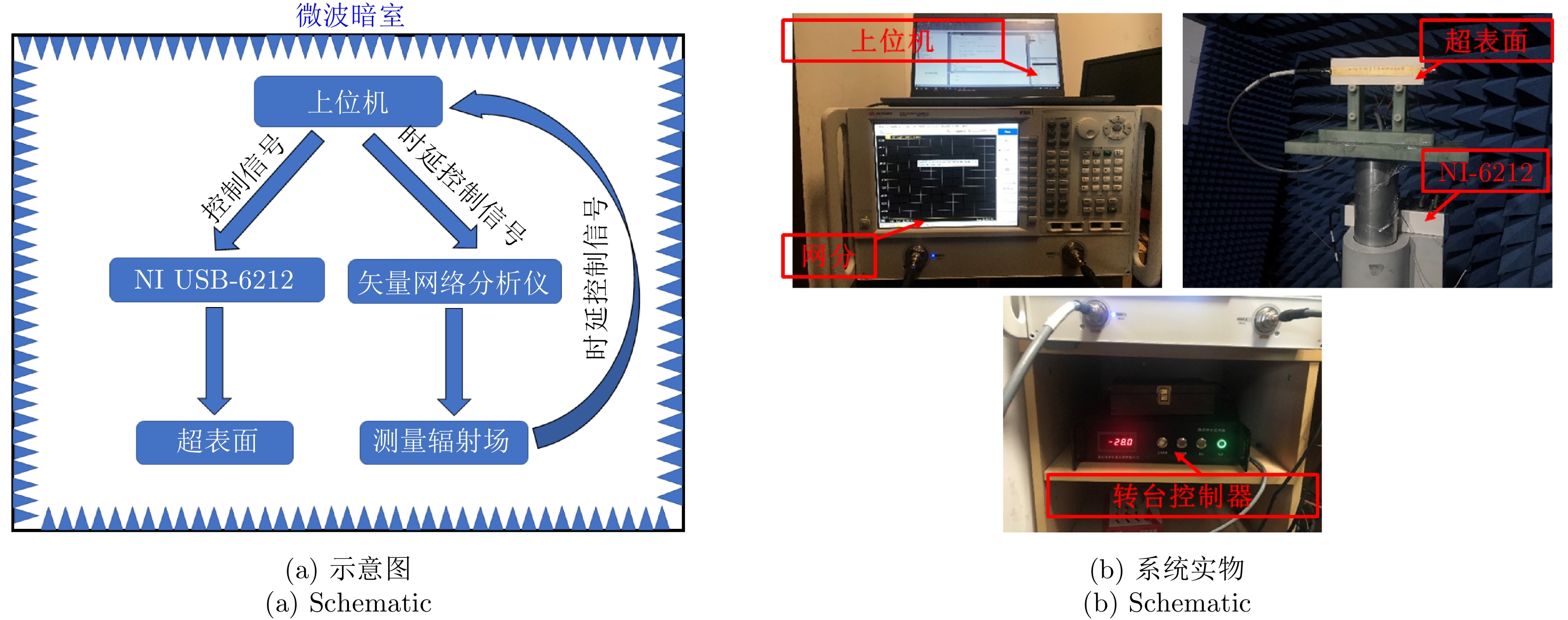
为了提供训练神经网络所需的数据集,本文设计了一套自动测试系统,自动切换编码的同时测试可编程超表面对应的辐射场。自动测试系统原理图和实物如图4所示,包括上位机、矢量网络分析仪、可编程超表面和NI USB-6212。NI USB-6212可与上位机通信并切换可编程表面上的直流偏置电压[5]。由于可编程超表面共有
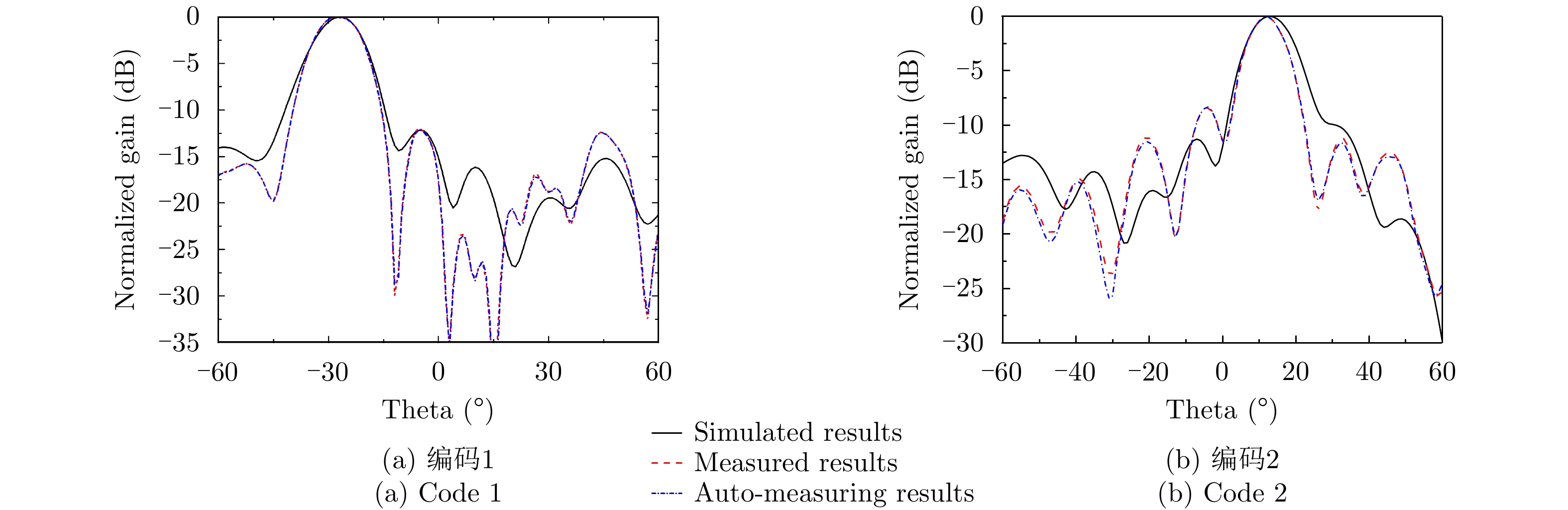
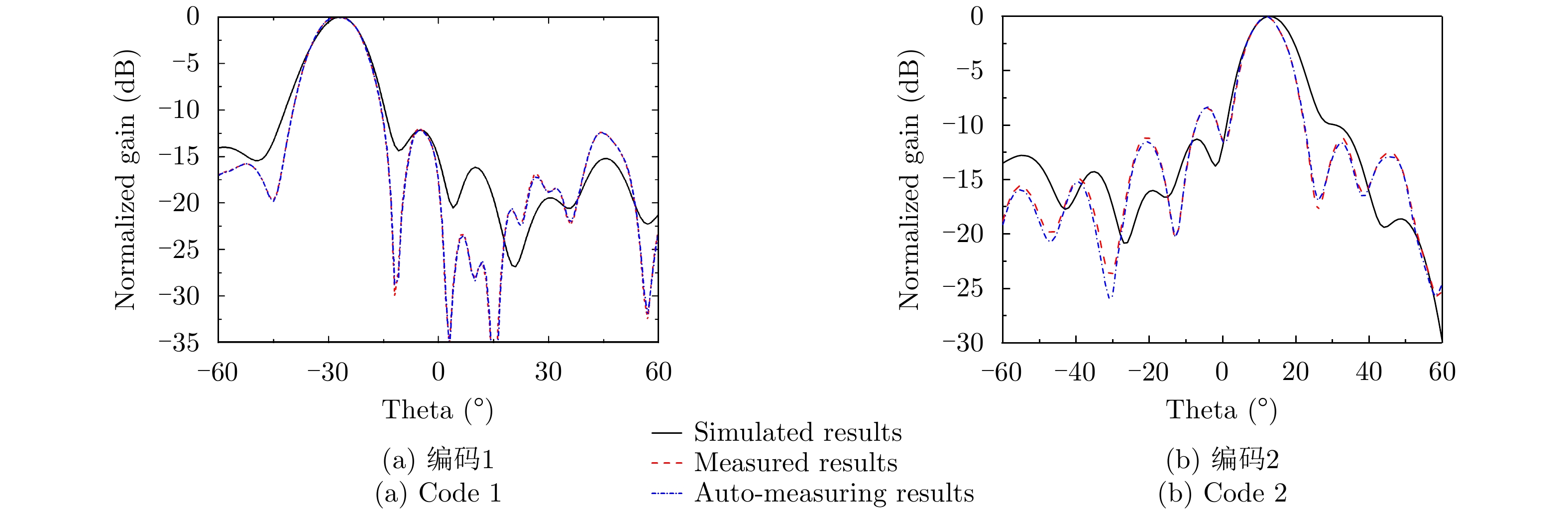
216 (65536)个不同的辐射场,我们利用自动测试系统随机选取16384个(占样本空间25%)不同的编码并测量其对应的辐射场数据。为了减少测试时间,我们仅对感兴趣的–60°~60°的辐射场数据测试。测试流程为:首先在起始角度,上位机控制NI USB-6212提供偏置电压给可编程超表面,经过0.02 s延迟后,上位机控制网络分析仪测试辐射场,经0.02 s延迟以后,上位机控制USB-6212切换辐射场并重复执行以上操作,直到在该角度下测完16384个编码的辐射场。然后利用上位机控制转台控制器切换到下一个角度,重复执行以上操作,直到测完–60°~60°所有编码的辐射场。经分析,自动测试系统的测量结果与实测方向图吻合良好。我们比较了编码1和编码2的HFSS仿真结果、实测结果和自动测试系统结果作为示例。如图5所示,自动测试系统的结果与实测值吻合良好,证明了设计的自动测试系统的正确性。值得注意的是,即使只测量了25%辐射场,仍然需要较长时间(约5天)。若利用自动测试系统测量整个样本空间的辐射场需要约20天以上,时间成本较高,对于单元数更多的超表面,将会消耗更多时间。基于测试获得的少量辐射场样本,利用神经网络可在不需要复杂前向物理模型的情况下,实现对剩下大量数据的准确高效预测。该方法对需要实时交互感知的应用具有重要意义。
3. 正向映射网络及预测结果
得益于深度学习算法的进步、硬件计算能力的提升,深度学习得到了越来越多的关注[6],近年来不断在语音、视频[7]等领域得到了大量的应用。然而在常见的无源天线、数字编码超材料方向图预测方向,深度学习的应用较为罕见,这是由于无源天线和数字编码超材料一旦制作完成,其辐射场为固定不变的。机器学习技术由大量的数据驱动,从数据中“学习”内在的物理规律。可编程超表面包含了许多主动器件,不同的数字编码序列对应不同的辐射场信息。不需要建立复杂的前向物理模型,利用深度学习技术可以很好地建立可编程超表面编码序列和辐射场的对应关系。
对于本文所提出超表面编码到辐射场的计算,传统方法例如离散偶极子近似,其基本原理是利用每个超表面单元处的总场等于入射场和其他单元产生的散射场在该处的叠加来求解最终的辐射场。但由于该算法中对格林函数的计算采用了近似值,导致对耦合效应的计算不准确,从而对最终的辐射场的计算存在偏差。为了快速求解所提出超表面辐射场,本文提出了一个深度神经网络,结构如图5所示。神经网络形式为全连接网络,由于神经网络可以从训练样本中准确的“学习”其物理规律,该方法可以准确建模不同编码下,超表面单元之间的耦合效应,从而实现对辐射方向图的精准预测,基于深度学习的方法优势在于:对于结构精细耦合效应复杂的超表面,传统的前向物理模型很难准确达到神经网络的预测效果,而深度学习算法可以克服该缺点。
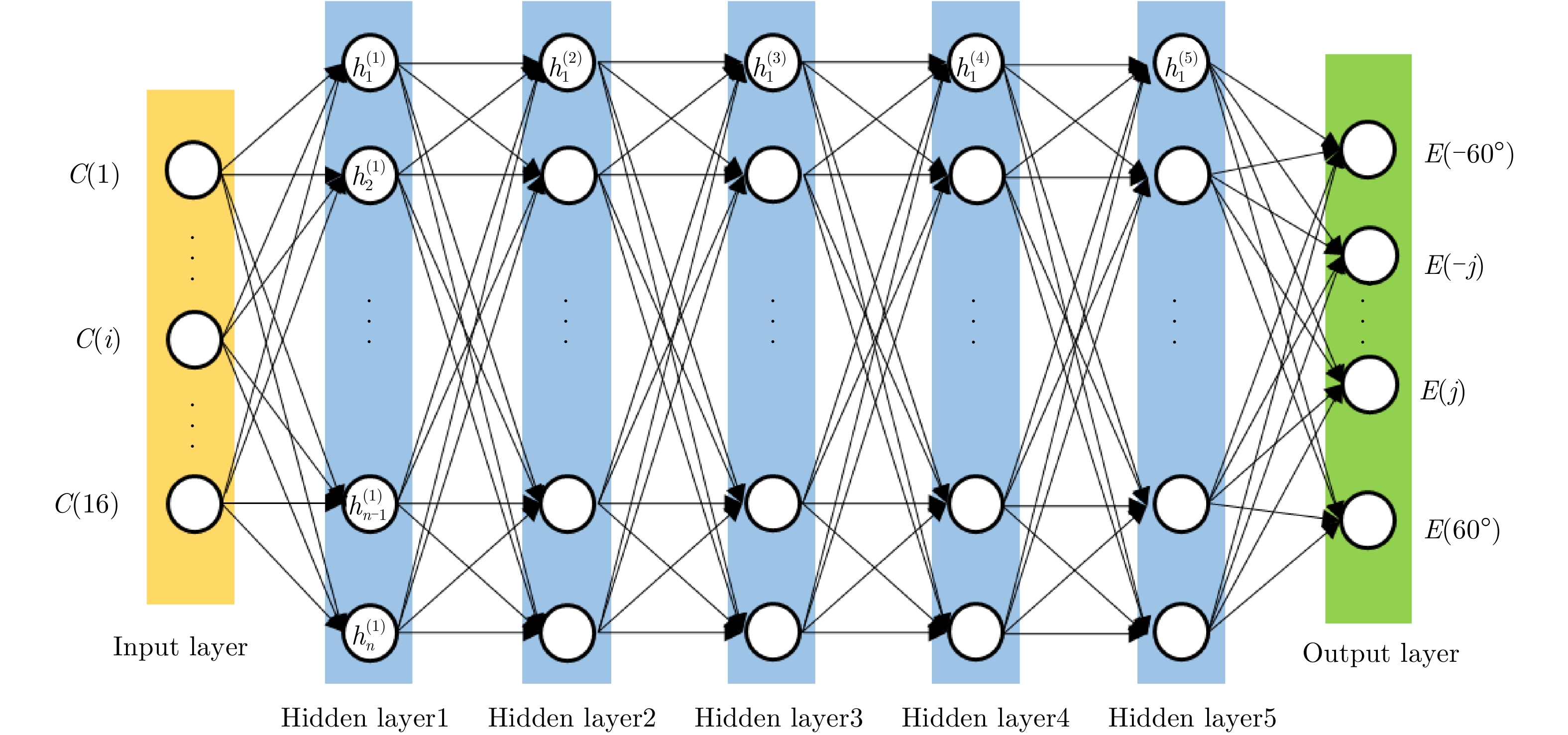
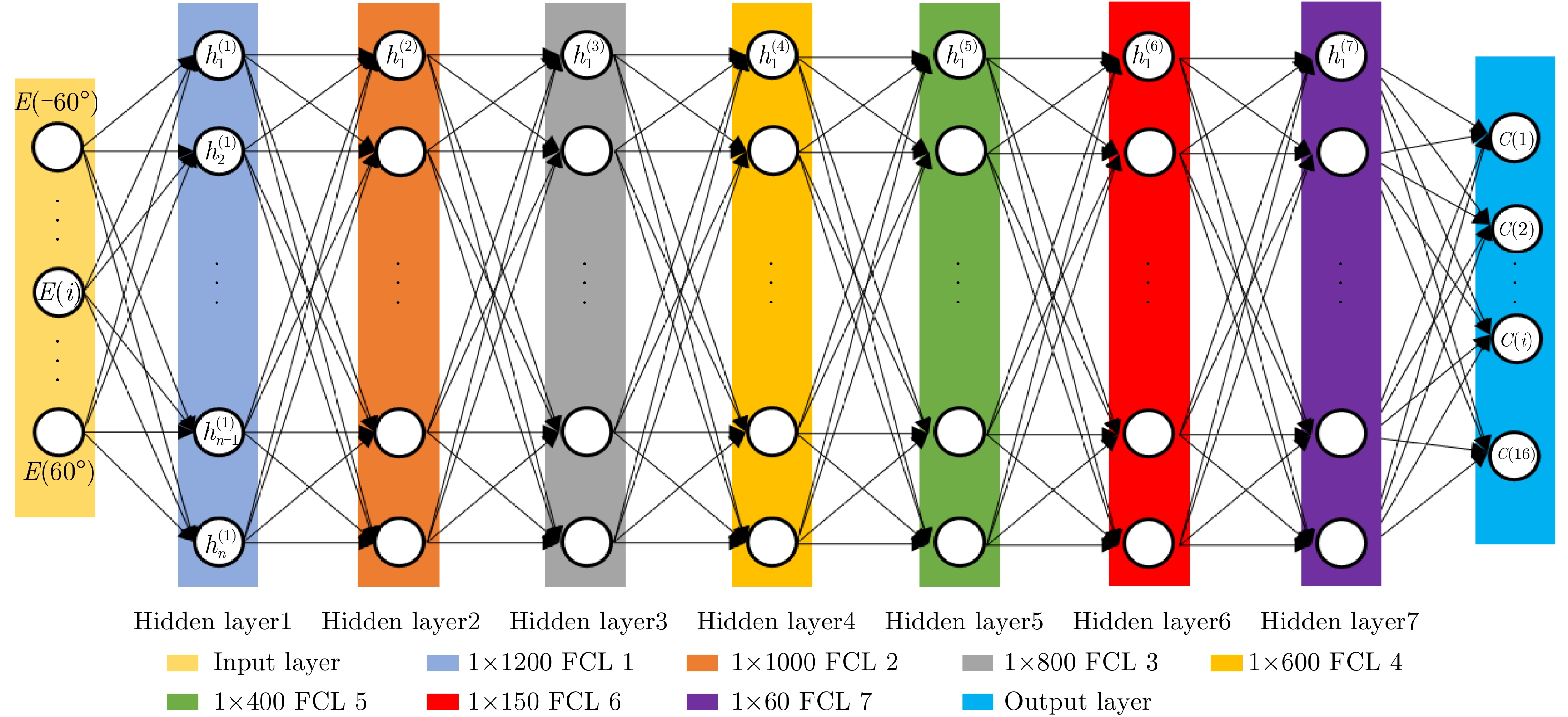
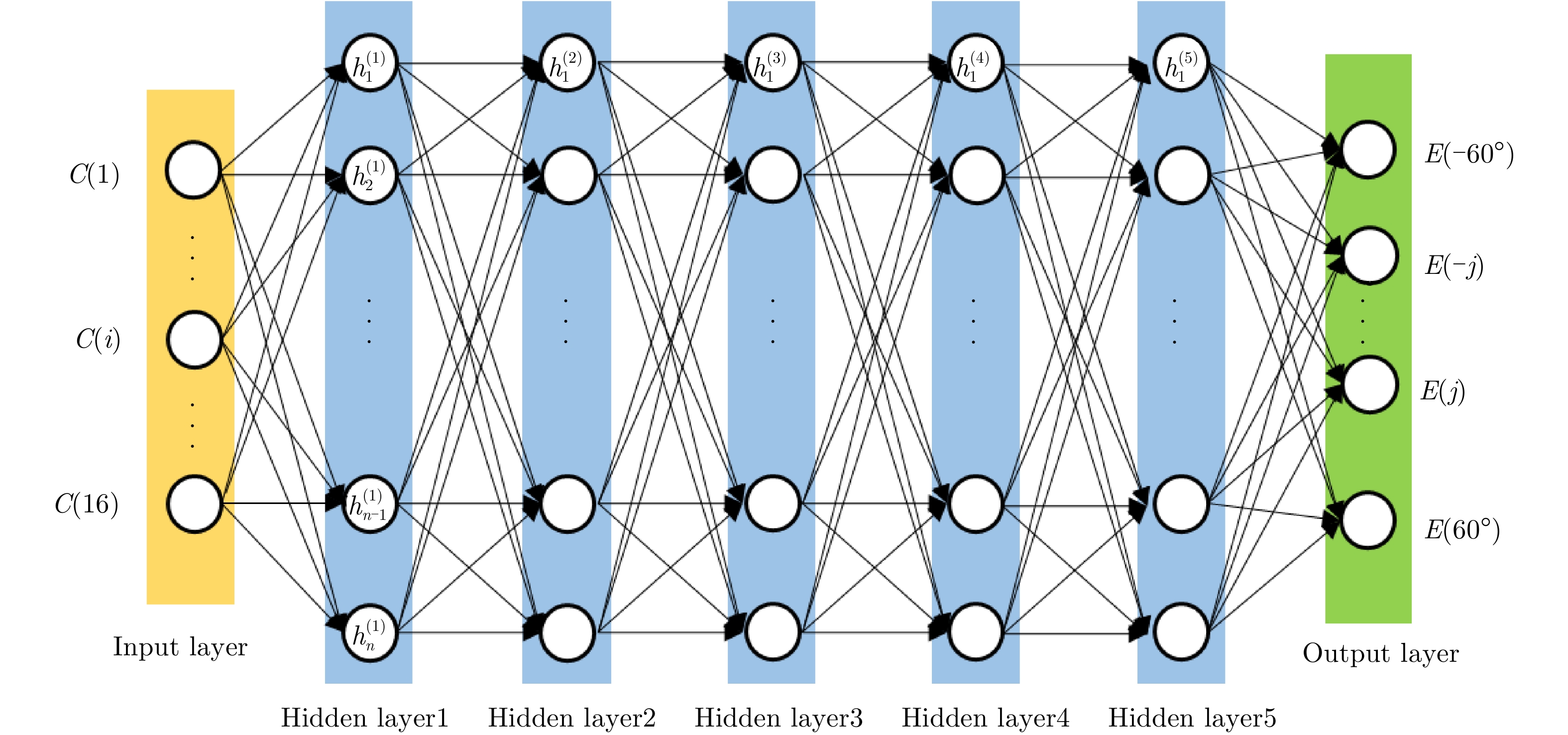
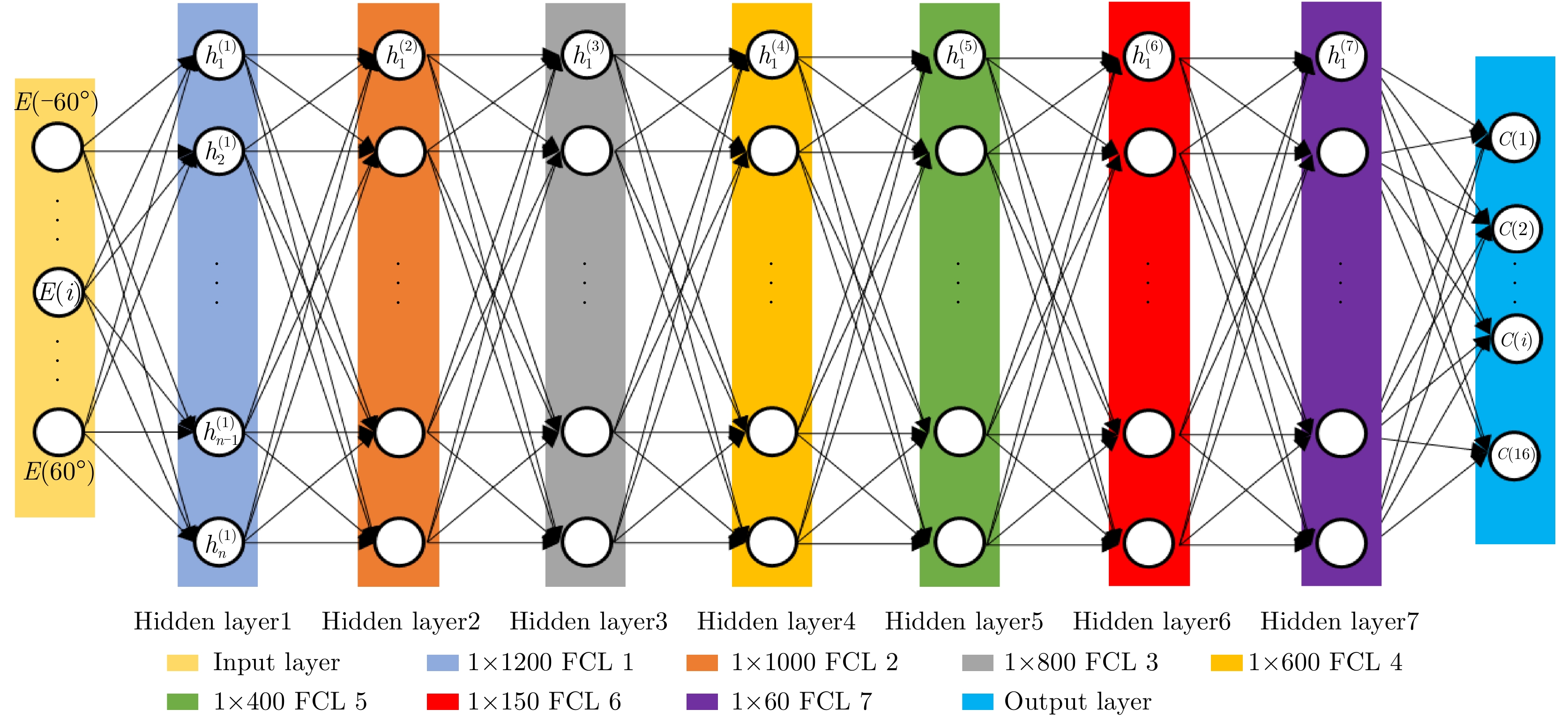
所提出网络结构如图6所示,输入层包含
16 个神经元,对应可编程超表面的16位编码序列,记为C(i), i为1~16的整数。网络包含5个隐藏层,从第1个到第5个隐藏层分别有1600, 1400, 1200, 800, 600个神经元,隐藏层中采用较多数目的神经元可以提高模型学习能力,网络采用线性整流函数(Rectified Linear Unit, ReLU)作为激活函数,隐藏层5 之后为包含121 个神经元的输出层,分别对应方向图中–60°~60°的辐射场[8]。训练过程的目标为最小化神经网络输出和真值之间的均方根误差RMSE,可表示为RMSE=√1nN∑i=1(ˆyi−yi)2 (1) 其中,n为样本个数,
ˆy 为神经网络预测值,y 为真值。训练过程中采用自适应矩估计法(Adaptive moment estimation, Adam)使得目标函数达到最小化。考虑到所提出超表面有16个单元,共有
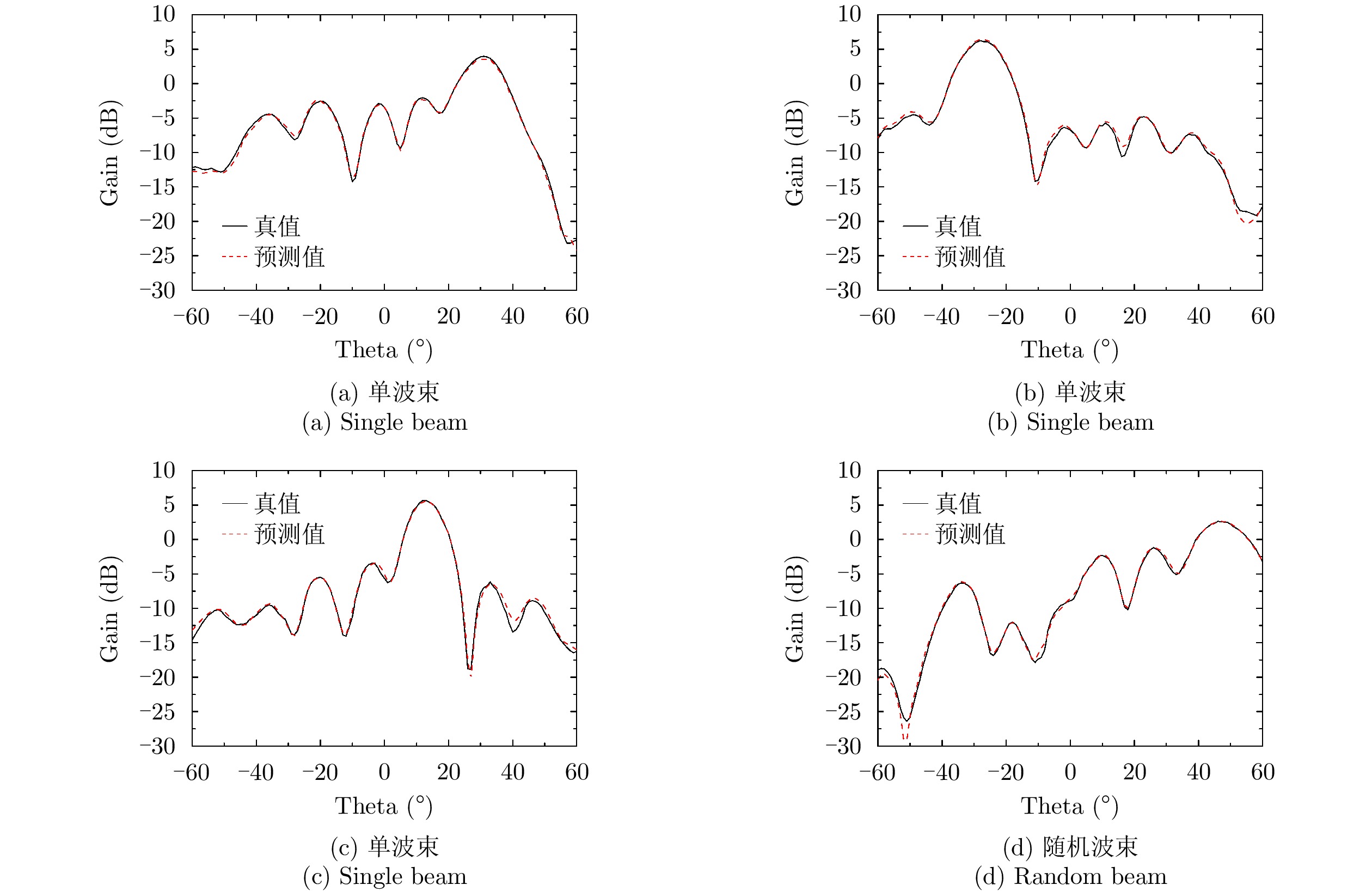
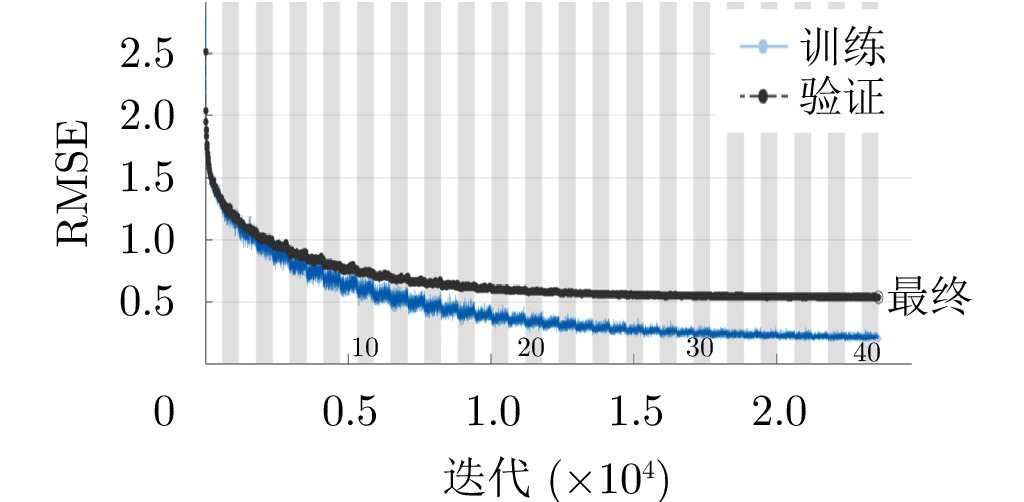
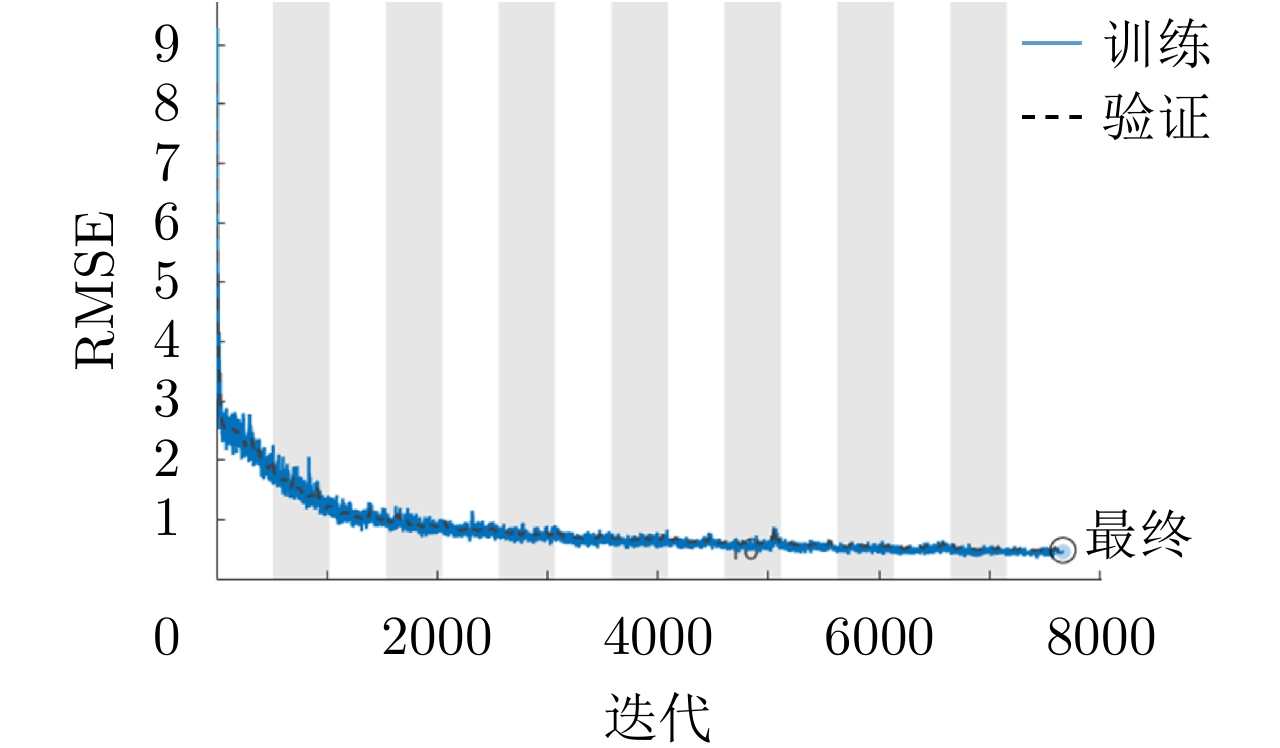
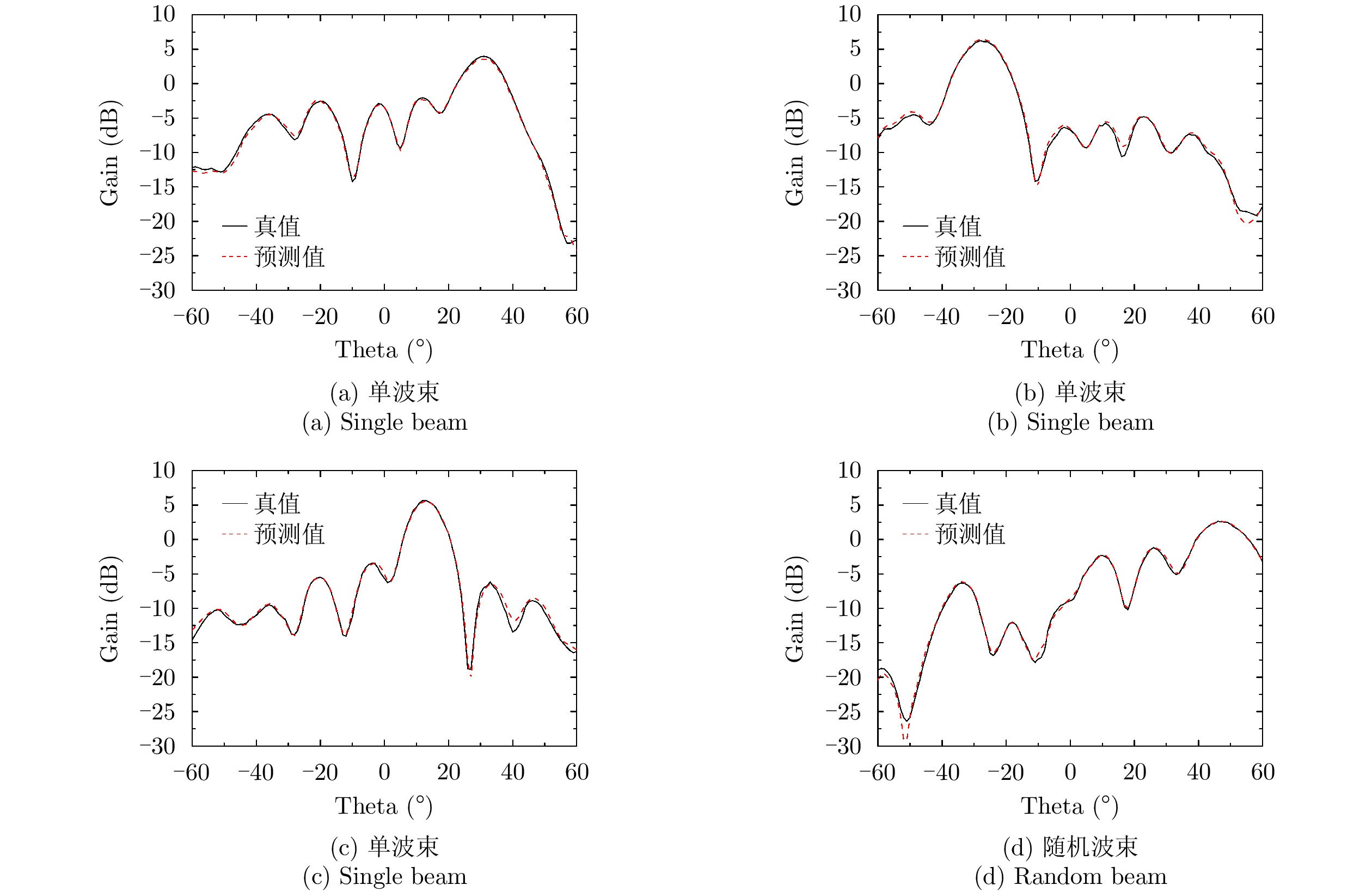
216 个不同的编码序列,对应216 =65536个不同的辐射场。我们利用自动测试系统测试整个样本空间1/4方向图样本的数据(16384个),取其中80%数据(13107个)作为训练样本,10%数据(1639个)作为验证数据,10%数据作为测试样本。训练过程均方误差随训练轮数结果如图7所示,随着迭代次数增加,网络模型收敛,最小均方误差为0.48。训练过程完成后,从测试样本中随机选取4个编码,利用神经网络预测方向图并与真值对比,其结果如图8所示。预测方向图和真值基本一致,对主瓣宽度和主瓣指向的预测较为准确。总体来看,利用该网络基本实现了仅有少量训练数据的情况下,准确预测所提出超表面的方向图。4. 逆向映射网络及反演结果
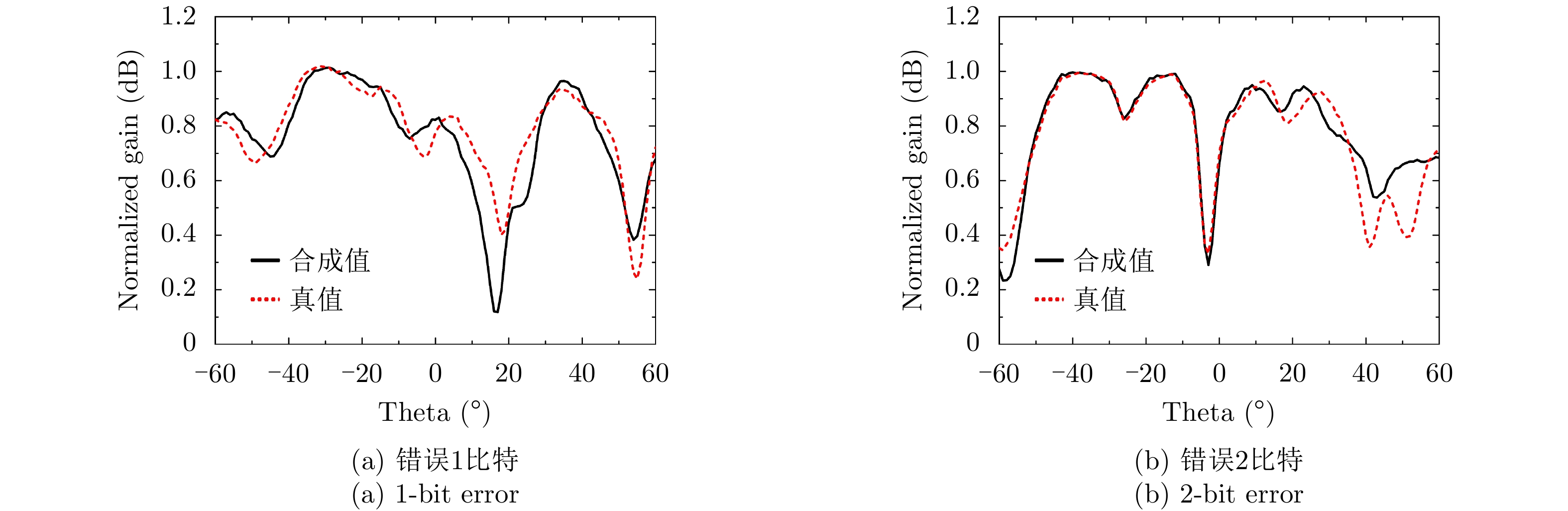
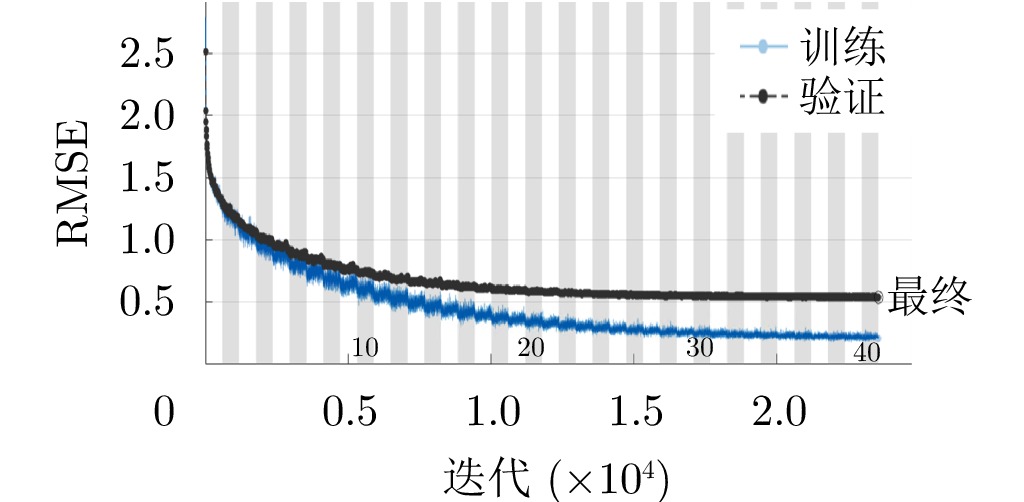
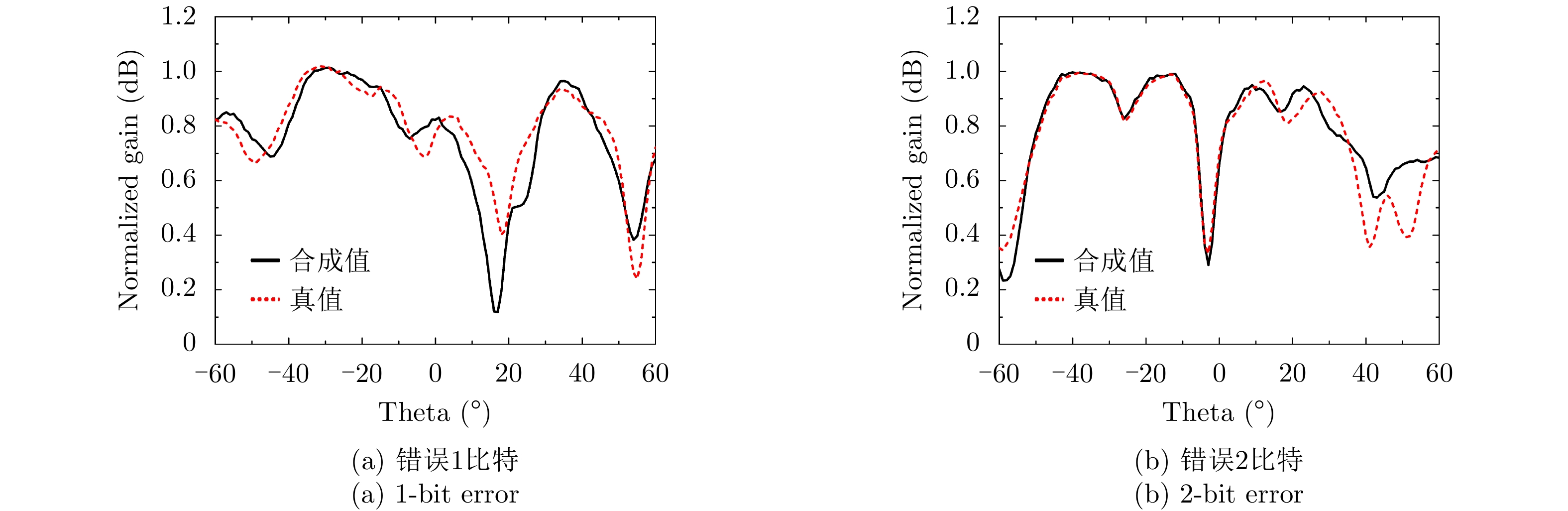
对于给定方向图反推编码的逆问题,传统的非线性优化算法可以解决该问题,但基于迭代的该类算法增加了计算复杂度,因而较难实现实时计算[9]。本文提出了另一个深度神经网络,通过增加网络层数实现对给定方向图准确实时预测其对应的编码。网络结构如图9所示,网络输入为–60°~60°的方向图数据,共有7层隐藏层,从隐藏层1到7分别有1200, 1000, 800, 600, 400, 150, 60个神经元,网络的输出为16位的编码,加深网络的层数可以提高编码预测准确率,网络激活函数为Leaky ReLU,训练采用Aadm算法。该网络对训练数据的要求比前向映射网络高,本文先利用前向神经网络预测了49150个方向图数据,再从实测数据中随机挑选9831个实测方向图数据,共同组成训练数据,测试数据为6553个实测方向图,训练过程的损失RMSE曲线如图10所示。为了直观展示预测错编码比特位数对方向图的影响,本文分别给出了预测错位1比特、2比特的方向图合成值和真值对比结果,为了减少测量方向图的时间,本文采用前向神经网络预测值作为合成值和真值比较。如图11所示,对于复杂波束,当预测错误1比特和2比特时,合成值和真值存在一定的偏差,但总体的趋势仍然比较接近。以上分析结果验证了所设计的深度神经网络的合理性。表4展示了深度神经网络计算的平均准确率
Accumean ,连续16位编码中错误0 比特准确率Accu0−bit ,错误1比特准确率Accu1−bit ,错误2比特准确率Accu2−bit ,错误3比特及以上准确率Accu3+bit 。神经网络对所有编码的计算平均准确率为99.09%,每个编码16位全正确的准确率为90.25%。对于一个Intel Core i7 - 8565U CPU @ 1.80 GHz配置的个人计算机,计算一个方向图到编码的平均时间为0.035 ms,在GPU加速的情况下该计算时间可以进一步被缩短。经过以上分析,给定方向图,所提出的网络可以实现实时准确预测其对应的编码序列。表 4 计算编码准确率Table 4. Accuracy for calculated codesAccumean Accu0−bit Accu1−bit Accu2−bit Accu3+bit 99.09% 90.25% 6.56% 2.12% 1.07% 5. 结论
针对可编程超表面编码和辐射场映射关系的快速求解,全波仿真软件耗时太长,传统算法计算复杂度高不能实时求解。本文通过设计一套辐射场自动测试系统,首先测试少量样本作为数据集,然后提出了前向的从编码到辐射场的深度神经网络,利用实测数据集作为训练数据训练前向网络,实现了对剩下辐射场的准确高效预测。利用该前向网络生成更多的辐射场数据,可训练逆向网络,即从辐射场到编码的映射网络,利用生成的数据和实测数据,实现了从辐射场到编码的实时准确求解。从而实现了可编程超表面基于神经网络的准实时智能波束形成。
-
表 1 超表面相关参数(mm)
Table 1. Parameters of the metasurface (mm)
L1 L2 L3 W1 offset d Wfeed Lg1 Lg2 Lg3 32.1 95 32.1 13 4 6 1.65 3.7 6.3 6 Lg4 Wg1 Wg2 Ls1 Ls2 Ws1 T D h1 h2 0.8 1.65 2.05 5 3.2 0.3 0.8 0.4 1.524 0.508 表 2 单波束编码
Table 2. Codes for single beams
编码号 编码序列 主瓣指向 波束宽度 Code 1 0101010101010101 –28° 13.5° Code 2 1001001001001001 13° 10.0° Code 3 1001100110011001 31° 8.5° 表 3 多波束编码
Table 3. Codes for multi-beam
编码号 编码序列 波束个数 Code 4 0001000100010001 2 Code 5 0000100001000010 3 Code 6 0000010000010000 4 表 4 计算编码准确率
Table 4. Accuracy for calculated codes
Accumean Accu0−bit Accu1−bit Accu2−bit Accu3+bit 99.09% 90.25% 6.56% 2.12% 1.07% -
[1] VESELAGO V G and LEBEDEV P N. The electrodynamics of substances with simultaneously negative values of ε and μ[J]. Soviet Physics Uspekhi, 1968, 10(4): 509–514. doi: 10.1070/PU1968v010n04ABEH003699 [2] PENDRY J B, HOLDEN A J, STEWART W J, et al. Extremely low frequency plasmons in metallic mesostructures[J]. Physical Review Letters, 1996, 76(25): 4773–4776. doi: 10.1103/PhysRevLett.76.4773 [3] CUI Tiejun, QI Meiqing, WAN Xiang, et al. Coding metamaterials, digital metamaterials and programmable metamaterials[J]. Light: Science & Applications, 2014, 3(10): e218. [4] LI Shangyang, XU Feng, WAN Xiang, et al. Programmable metasurface based on substrate-integrated waveguide for compact dynamic-pattern antenna[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(5): 2958–2962. doi: 10.1109/TAP.2020.3023581 [5] https://www.ni.com/zh-cn/support/model.usb-6212.html. [6] SAINATH T N, MOHAMED A R, KINGSBURY B, et al. Deep convolutional neural networks for LVCSR[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, Canada, 2013: 8614–8618. [7] TOMPSON J, JAIN A, LECUN Y, et al. Joint training of a convolutional network and a graphical model for human pose estimation[C]. The 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 1799–1807. [8] PULIDO-MANCERA L M, ZVOLENSKY T, IMANI M F, et al. Discrete dipole approximation applied to highly directive slotted waveguide antennas[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1823–1826. doi: 10.1109/LAWP.2016.2538202 [9] SHAN Tao, PAN Xiaotian, LI Maokun, et al. Coding programmable metasurfaces based on deep learning techniques[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2020, 10(1): 114–125. doi: 10.1109/JETCAS.2020.2972764 期刊类型引用(3)
1. 潘宇轩,蒋伊琳,闫成越,李金鑫. 基于强化学习的异常反射编码超表面设计. 哈尔滨商业大学学报(自然科学版). 2025(01): 38-42 .  百度学术
百度学术2. 院琳,唐佳,于海洋,张城. 基于人工神经网络的高效电磁诱导透明超表面阵列设计. 新一代信息技术. 2023(14): 1-4 .  百度学术
百度学术3. 刘星,封华伟. 6G通信时代产业生态典型机会探析. 中国科技产业. 2022(05): 55-57 .  百度学术
百度学术其他类型引用(4)
-



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公


 下载:
下载:


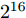


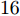
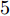
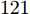

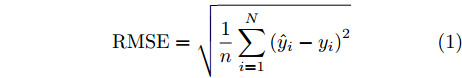
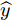
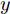
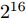
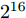


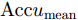
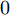
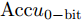
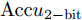
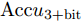



 下载:
下载:
 百度学术
百度学术