1 引言
逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)利用测量时间内目标相对雷达视线的姿态变换产生合成孔径获得方位高分辨,同时通过发射带宽信号来获得距离高分辨。为了避免不同目标散射点回波的脉冲交叠和互干扰问题,通常ISAR系统发射线性调频波形[1]和步进频波形[2]等宽带波形。在成像接收端,由于散射信号模糊函数旁瓣的影响,距离单元间干扰(Inter-Range-Cell Interference, IRCI)仍然存在,IRCI抑制是高分辨成像中的重大问题。为解决雷达成像中IRCI问题,依托无线通信中正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)解决码间干扰问题的方法,OFDM技术引入到雷达成像领域。传统OFDM雷达发射信号无循环前缀(Cyclic Prefix, CP)插入,接收端采用匹配滤波[3, 4, 5],由于信号旁瓣的影响,与普通雷达信号一样IRCI依然存在。为改善这一问题,基于CP的OFDM信号及无IRCI距离向重构问题目前已提出[6, 7],通过插入足够长度的CP,可以对IRCI进行有效抑制,但此方法目前主要针对SAR成像,ISAR方面的应用目前处于初级阶段。ISAR成像针对的通常是非合作目标,需要运动补偿来克服包络走动和图像散焦。运动补偿通常包含两个步骤:包络对齐和相位校正[8, 9]。包络对齐是用来粗略地校正运动误差,可通过最大相关法和全局优化法实现。相位校正是用来消除高阶相位误差项,其方法大概可分为两类:第1类方法是基于显性散射点的相位追踪方法,这类方法着眼于独立散射点的相位历程,当在高杂波和信噪比较低的环境中,算法性能下降。另一类算法从图像质量的角度估计相位误差,比如加权最小二乘法估计(Weighted Least-Squares Estimation, WLSE)和最小熵相位校正。这些方法利用图像中所有散射点来估计相位误差,因此,这类方法对噪声有很强的鲁棒性。随着稀疏信号处理理论的发展,未知自聚焦稀疏ISAR图像可通过解决优化问题从有限测量数据中被恢复。OFDM信号对频偏和运动误差更为敏感,针对OFDM-ISAR成像需要联合考虑无IRCI距离像综合和相位补偿问题,相比传统ISAR成像难度更大。
稀疏信号处理理论[10]已成功应用于ISAR成像和相位校正[11, 12, 13, 14],本文将其拓展到OFDM-ISAR的成像处理。与现有的无IRCI距离像重构相比,利用了ISAR成像的本质稀疏性,本文稀疏优化的算法联合考虑到各距离单元间IRCI和目标运动误差。在优化求解方面,本文同时建立了利用快速傅里叶变换的高效求解方法。
2 基于CP的OFDM-ISAR信号模型
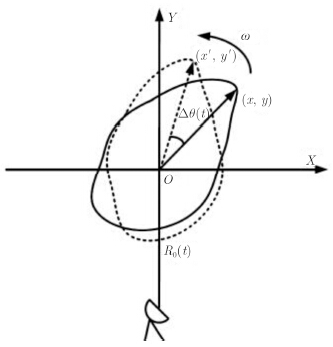
ISAR成像几何如图 1所示,雷达与目标之间的相对运动可分为平动和转动,仅转动分量对ISAR成像有贡献而平动分量应该被补偿。目标区域可被划分为${x_m} = m{\rho _x}$ (m=0, 1, $\cdots$, M-1)和${y_h} = h{\rho _y}$ (h=0, 1, $\cdots$, H-1) (${\rho _x}$和${\rho _y}$分别为方位向和距离向分辨率)。我们假设OFDM信号有N个子载波且带宽为B。
|
\[S\left( \tau \right) = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {W_k}\exp \left( {{\rm{j}}2\pi k\Delta f\tau } \right),\quad 0 \le \tau \le T\]
| (1) |
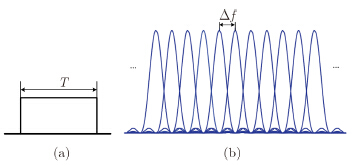
其中,${W_k}\left( {k = 0, 1, \cdots, N - 1} \right)$是调制符号,对应着第k子载波的复权值$\sum\nolimits_{k = 0}^{N - 1} {{{\left| {{W_k}} \right|}^2}} = N$ 。T是不包含CP的OFDM信号长度,$\Delta f$为子载波间隔。为避免OFDM子载波间干扰,需要保持子载波正交性,这就需要每个子载波的频域结构与子载波间隔相结合,如图 2所示,满足1/T=$\Delta f$。假设OFDM采样间隔为Ts=T/N=1/B,则OFDM信号可通过对权向量逆傅里叶变化方式获得。
根据这一假设,离散采样OFDM信号表示为:
|
\[\begin{array}{l}
S\left( {n{T_{\rm{s}}}} \right) = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {{W_k}\exp \left( {{\rm{j}}2\pi \frac{{kn}}{N}} \right)} ,\\
\quad \quad \quad \quad \quad \quad 0 \le n \le N - 1
\end{array}\]
| (2) |
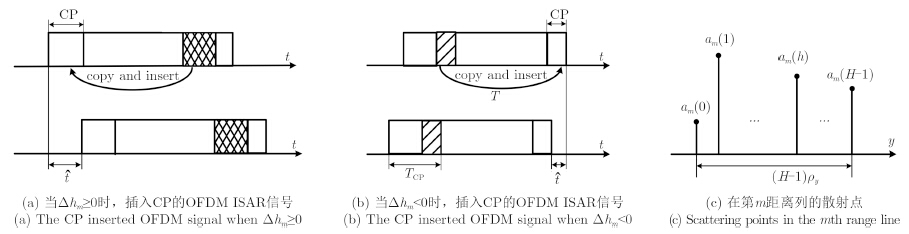
离散OFDM信号${{s}} \!=\! {[\begin{array}{*{20}{c}} \!\! {S\left( 0 \right)} \, {S\left( {{T_{\rm s}}} \right)} \, \, \cdots \, \, {S\left( {(N \!\!-\!\! 1){T_{\rm s}}} \right)} \!\! \end{array}]^{\rm{T}}}$为权向量${{w}} = {[\begin{array}{*{20}{c}} \!\! {{W_0}} \, \, \, {{W_1}} \, \, \cdots \, \, {{W_{N - 1}}} \!\! \end{array}]^{\rm{T}}}$的N点信号矢量。对于非合作目标,目标平动带来的距离向偏移会降低OFDM成像的质量,与文献[6]中的忽略距离偏移误差的方法不同,通过插入足够长度的CP,本文提出了针对非合作目标的无IRCI的距离像重构算法。假设距离向有H个距离单元,Δhm是第m个距离列由于平动引起的距离偏移分辨率数目,$\Delta {h_{\max }} = \mathop {\max }\limits_m \{ |\Delta {h_m}|\} $。为避免所有距离列的IRCI,保证回波信号的正交性,CP的长度需要满足${N_{\rm{CP}}} \ge H + 2\Delta {h_{\rm max}} - 1$[6],在这种情况下,一个距离列的所有距离单元的回波时间延迟$\hat t$不会超过TCP,发射信号的模拟长度为T+TCP。CP插入的具体过程如图 3(a),图 3(b)所示。与基于CP的SAR成像[6, 7]相比,此处CP的长度不仅与距离单元有关,还要考虑平动误差的影响。
考虑到载频fc的影响,发射OFDM-ISAR信号可表示为:
|
\[\begin{array}{l}
{S_{{\rm{tr}}}}\left( \tau \right) = S\left( \tau \right)\exp \left( {{\rm{j}}2\pi {f_{\rm{c}}}\tau } \right)\\
\quad \quad \quad = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {{W_k}\exp \left[ {{\rm{j}}2\pi ({f_{\rm{c}}} + k\Delta f)\tau } \right]} ,\\
\quad \quad \quad \quad \quad \quad 0 \le \tau \le T + {T_{{\rm{CP}}}}
\end{array}\]
| (3) |
在基频压缩之后,目标的第m距离列回波脉冲可用快时间τ和慢时间tm表示为:
|
\[\begin{array}{l}
{G_m}\left( {\tau ,{t_m}} \right) = \sum\limits_{h = 0}^{H - 1} {{a_m}} \left( h \right)\exp \left( { - {\rm{j}}\frac{{4\pi {R_{mh}}\left( {{t_m}} \right)}}{\lambda }} \right)\\
\quad \quad \quad \quad \cdot \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {W_k}\exp \left[ {{\rm{j}}2\pi k\Delta f\left( {\tau - \frac{{2{R_{mh}}\left( {{t_m}} \right)}}{c}} \right)} \right]
\end{array}\]
| (4) |
其中λ=c/fc是发射信号波长,c是光速。am(h)是成像平面中第m距离列中第h个散射点的后向散射系数,如图 3(c)所示。Rmh(tm)是坐标为(xm, yh)=(mρx, hρy)的散射点到雷达的瞬时距离,可表示为:
|
\[{R_{mh}}\left( {{t_m}} \right) = {R_0}\left( {{t_m}} \right) + {y_h}\cos \Delta \theta \left( {{t_m}} \right) + {x_m}\sin \Delta \theta \left( {{t_m}} \right)\]
| (5) |
其中
R0(
tm)是第
m(0≤
m≤
M)个回波目标旋转中心到雷达的距离,Δ
θ(
tm)是旋转角,假设转速
ω在CPI内保持不变,则转角可表示为Δ
θ(
tm)=
ωtm, tm=m(
T+
TCP),
T+
TCP是脉冲重复周期。在CPI内,转角较小,我们可得到如下假设sinΔ
θ(
tm)≈
ω(
tm)和cosΔ
θ(
tm)≈1。式(4)中$\tau - \frac{{2{R_{mh}}\left( {{t_m}} \right)}} c$项可表示为:
|
\[\begin{array}{l}
\tau - \frac{{2{R_{mh}}\left( {{t_m}} \right)}}{c} = \tau - \frac{{2[{R_0}\left( {{t_m}} \right) + {y_h} + {x_m}\Delta \theta \left( {{t_m}} \right)]}}{c}\\
\quad \quad \quad \quad \quad = \tau - \frac{{2{y_h}}}{c} - \frac{{2[{R_0}\left( {{t_m}} \right) + {x_m}\Delta \theta \left( {{t_m}} \right)]}}{c}\\
\quad \quad \quad \quad \quad = \tau - h{T_{\rm{s}}} - {t_{m0}}
\end{array}\]
| (6) |
小角度ISAR成像可假设转动引起的越距离单元徙动可忽略,则时间延迟2R0(tm)/c对应平动引起的第m距离列的距离偏移误差,其可近似为$\Delta {h_m}{T_{\rm s}}$。在$\tau \! = \! l \ {T_{\rm s}}(l = 0, 1, \cdots, N \! + \! {N_{\rm CP}} \! + \! H \! - \! 2)$ 处采样,第m距离列的脉冲回波可近似表示为:
|
\[\begin{array}{l}
{G_m}\left( l \right) = \sum\limits_{h = 0}^{H - 1} {{a_m}} \left( h \right)\exp \left( { - {\rm{j}}\frac{{4\pi {R_{mh}}\left( {{t_m}} \right)}}{\lambda }} \right)\\
\quad \quad \quad \cdot \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {W_k}\exp \left[ {{\rm{j}}2\pi k\Delta f\left( {l{T_{\rm{s}}} - h{T_{\rm{s}}} - \Delta {h_m}{T_{\rm{s}}}} \right)} \right]\\
\quad \quad = \sum\limits_{h = 0}^{H - 1} {{U_m}} \left( h \right)\tilde S\left( {l - h - \Delta {h_m}} \right),\\
\quad \quad \quad \quad l = 0,1, \cdots ,N + {N_{{\rm{CP}}}} + H - 2
\end{array}\]
| (7) |
其中${U_m}\left( h \right) \! = \! {a_m}\left( h \right)\exp \left( \! {- {\rm j}\frac{{4\pi {R_{mh}}\left( {{t_m}} \right)}}{\lambda }} \right)$, $\tilde S\left( i \right)$ 为插入CP的OFDM信号,可表示为:
|
\[\begin{array}{l}
\tilde S(i) = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {{W_k}\exp [{\rm{j}}2\pi k\Delta fi{T_{\rm{s}}}]} \\
\quad \quad = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {{W_k}\exp \left( {{\rm{j}}2\pi \frac{{ki}}{N}} \right)} ,\\
\quad \quad \quad \quad \quad i = 0,1, \cdots ,N + {N_{{\rm{CP}}}} - 1
\end{array}\]
| (8) |
第m距离列距离单元回波信号长度为$N + {N_{\rm{CP}} } + H - 1$。IRCI可在前NCP个采样中出现,为得到无IRCI的图像,前NCP个采样需要被移除,同时,残余信号的后H-1个采样不能完全反映H个散射点后向散射系数,所以,在雷达接收端,移除CP后还需移除后H个采样值,从而第m距离列回波信号为:
|
\[\begin{array}{l}
{G_m}\left( {l + {N_{{\rm{CP}}}}} \right) = \sum\limits_{h = 0}^{H - 1} {{U_m}} \left( h \right)\tilde S\left( {l + {N_{{\rm{CP}}}} - h - \Delta {h_m}} \right),\\
\quad \quad \quad \quad \quad \quad \quad \;l = 0,1, \cdots ,N - 1
\end{array}\]
| (9) |
信号的矩阵形式表达如下:
|
\[\begin{array}{*{20}{l}}
{\left[ {\begin{array}{*{20}{c}}
{{G_m}\left( {{N_{{\rm{CP}}}}} \right)}&{{G_m}\left( {{N_{{\rm{CP}}}} + 1} \right)}& \cdots &{{G_m}\left( {{N_{{\rm{CP}}}} + N - 1} \right)}
\end{array}} \right]}\\
{ = \left[ {\begin{array}{*{20}{c}}
{{U_m}\left( 0 \right)}&{{U_m}\left( 1 \right)}& \cdots &{{U_m}\left( {H - 1} \right)}
\end{array}} \right]}\\
{ \times \left[ {\begin{array}{*{20}{c}}
{S({N_{{\rm{CP}}}} - \Delta {h_m})}&{\tilde S({N_{{\rm{CP}}}} - \Delta {h_m} + 1)}& \cdots &{\tilde S({N_{{\rm{CP}}}} - \Delta {h_m} + N - 1)}\\
{S({N_{{\rm{CP}}}} - \Delta {h_m} - 1)}&{\tilde S({N_{{\rm{CP}}}} - \Delta {h_m})}& \cdots &{\tilde S({N_{{\rm{CP}}}} - \Delta {h_m} + N - 2)}\\
\vdots & \vdots & \ddots & \vdots \\
{S({N_{{\rm{CP}}}} \!\!- \!\! \Delta {h_m}\!\!-\!\! H \!\!+ \!\!1)}&{\tilde S({N_{{\rm{CP}}}} \!\!-\!\! \Delta {h_m} \!\!-\!\! H \!\!+\!\! 2)}& \cdots &{\tilde S({N_{{\rm{CP}}}} \!\!- \!\!\Delta {h_m}\!\! -\!\! H \!\!+\!\! N)}
\end{array}} \right]}\\
{ = \left[ {\begin{array}{*{20}{c}}
{{U_m}*{{({{\tilde s}_m})}_{H - 1}}}
\end{array}} \right]}
\end{array}\]
| (10) |
其中${\left( {{{\tilde s}_m}} \right)_{H - 1}} = \left[ {\tilde S\left( {{N_{{\rm{CP}}}} - \Delta {h_m}} \right)} \right.\;\;\tilde S\left( {{N_{{\rm{CP}}}} - \Delta {h_m} + 1} \right) \cdots \;\;\left. {\tilde S\left( {{N_{{\rm{CP}}}} - \Delta {h_m} + N - 1} \right)} \right]$,则回波信号为:
|
\[G = \left[ {\begin{array}{*{20}{c}}
{{g_0}}\\
{{g_1}}\\
\vdots \\
{{g_{M - 1}}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{u_0}*{{\left( {{{\tilde s}_0}} \right)}_{H - 1}}}\\
{{u_1}*{{\left( {{{\tilde s}_1}} \right)}_{H - 1}}}\\
\vdots \\
{{u_{M - 1}}*{{\left( {{{\tilde s}_{M - 1}}} \right)}_{H - 1}}}
\end{array}} \right]\]
| (11) |
OFDM可对向量
gm进行(快速傅里叶变换)FFT解调,对
gm的FFT结果可表示为:
|
\[{\rm{FFT}}\left( {{g_m}} \right) = {\rm{FFT}}\left( {{u_m}} \right) \cdot {\rm{FFT}}\left( {{{\tilde w}_m}} \right)\]
| (12) |
其中FFT(·)为向量
N点FFT, ${\rm{FFT}}\left( {{u_m}} \right)\left( k \right) = \sqrt N \sum\nolimits_{n = 0}^{N - 1} {{U_m}} \left( n \right){\rm{exp}}\left( { - {\rm{j}}2\pi \frac{{kn}}{N}} \right)。{\rm{FFT}}\left( {{{\tilde w}_m}} \right)$是向量${\left( {{{\tilde s}_m}} \right)_{H - 1}}$的FFT,注意到$\tilde S$的周期性以及$ {\left({{{\tilde {{s}}}_m}} \right)_{H - 1}} \! = \! \left[{\tilde S \! \left( {{N_{\rm CP}} \! - \! \Delta {h_m}} \right), \tilde S\left( {{N_{\rm CP}} \! - \! \Delta {h_m} \! + \! 1} \right), \cdots, } \right.$ $ \tilde S\left( {N \! - \! 1} \right), {\tilde S\left( 0 \right), \tilde S\left( 1 \right), \cdots, \tilde S\left( {{N_{\rm CP}} - \Delta {h_m} \!-\! 1} \right)}$,本质上为向量 $\tilde S$的${N_{{\rm{CP}}}} - \Delta {h_m}$的循环平移。
从上文的讨论可知,s对应向量ω的逆傅里叶变换,在雷达接收端,在没有Δhm项的前提下,权向量ω的设计可与文献[6, 7]中相同,${\tilde W_k}$可表示为:
|
\[{\tilde W_k} = {W_k}\exp \left( {{\rm{j}}2\pi \frac{{\left( {{N_{{\rm{CP}}}}} \right)k}}{N}} \right),\;k = 0,1, \cdots ,N - 1\]
| (13) |
则${\mathop{\rm FFT}\nolimits} \left( {{{{u}}_m}} \right)$可通过下式估计:
|
\[\begin{array}{*{20}{c}}
{{\rm{FFT}}\left( {{u_m}} \right)\left( k \right) = \frac{{{\rm{FFT}}\left( {{g_m}} \right)\left( {k} \right)}}{{{{\tilde W}_k}}} = \frac{{{\rm{FFT}}\left( {{g_m}} \right)\left( {k} \right)}}{{{W_k}\exp \left( {{\rm{j}}2\pi \frac{{\left( {{N_{{\rm{CP}}}}} \right)k}}{N}} \right)}},}\\
{k = 0,1, \cdots ,N - 1}
\end{array}\]
| (14) |
通过对${\mathop{\rm FFT}\nolimits} \left( {{{{u}}_m}} \right)$做N点IFFT可得到Um,考虑到Δhm的影响,第m距离列的距离像可表示为:
|
\[\begin{array}{l}
{U_m}\left( {\tau ,{t_m}} \right) = \sum\limits_{k = 0}^{N - 1} {{{\hat a}_m}} \left( k \right)\delta \left( {\tau - k{T_{\rm{s}}} - \Delta {h_m}{T_{\rm{s}}}} \right)\\
\quad \quad \quad \quad \quad \cdot \exp \left( { - {\rm{j}}\frac{{4\pi {R_{mh}}\left( {{t_m}} \right)}}{\lambda }} \right)
\end{array}\]
| (15) |
文献[6, 7]描述了OFDM雷达成像与通信系统的相似性,指出雷达应用子载波的数量至少为目标覆盖的距离单元数,也就是N≥H。如果N>H,得到的式(15)中的向量${\hat {a}_m}$有一些零值,$\left[{{{\hat a}_m}\left( {H - 1} \right), \cdots, {{\hat a}_m}\left( {N - 1} \right)} \right]$部分为不存在的后向散射系数。如果N=H,向量${\hat {a}_m}$的估计恰好等于第m距离列的散射点后向散射系数。当N<H,由于傅里叶变换的周期性,式(10)中的每一列向量均大于1个周期,Gm的估计来自于不同距离单元的和,IRCI出现。因此,OFDM信号子载波的数量N至少等于H。同时,为完全避免不同距离单元间的IRCI, CP的长度也需要如本文前面分析的一样进行适当选择。在ISAR成像中,距离单元为发射带宽的函数,由于子载波的数量N至少等于距离单元数H,高分辨的无IRCI的距离像可获得,其分辨率为${\rho _y} = c/\left( {2B} \right)$。
对于OFDM-ISAR成像而言,对目标平动补偿的精确校正至关重要。本文采用相关包络对齐估计目标平动参数,为了最大限度地获得好的包络对齐效果,通过2次拟合来压制信号的跳变,拟合函数的1次和2次系数分别对应着非合作目标的速度和加速度分量,我们可获得时间延迟$\Delta {h_m}{T_{\rm s}}$的估计,为得到无IRCI的距离像,$\Delta {h_m}$被近似为整数。包络对齐后,在同一距离的散射点被校正到相同的距离单元,无IRCI的距离像可表示为:
|
\[\begin{array}{l}
U\left( {\tau ,{t_m}} \right) = \sum\limits_{m = 0}^{M - 1} {\sum\limits_{k = 0}^{N - 1} {{{\hat a}_m}} } \left( k \right)\delta \left( {\tau - k{T_{\rm{s}}}} \right)\\
\quad \quad \quad \quad \cdot \exp \left( { - {\rm{j}}\frac{{4\pi {R_{mk}}\left( {{t_m}} \right)}}{\lambda }} \right)
\end{array}\]
| (16) |
3 稀疏优化的OFDM-ISAR相位校正
式(16)中U的相位项反映了OFDM回波信号的方位向信息,把式(5)式代入式(16),信号转变为:
|
\[\begin{array}{l}
U\left( {\tau ,{t_m}} \right) \approx \sum\limits_{m = 0}^{M - 1} {\sum\limits_{k = 0}^{N - 1} {{{\hat a}_m}} } \left( k \right)\delta \left( {\tau - k{T_{\rm{s}}}} \right)\\
\quad \quad \quad \quad \cdot \exp \left( { - {\rm{j}}\frac{{4\pi \left( {{R_0}({t_m}) + {y_k} + {x_m}\omega {t_m}} \right)}}{\lambda }} \right)\\
\quad \quad \quad = \sum\limits_{m = 0}^{M - 1} {\sum\limits_{k = 0}^{N - 1} \exp } \left( { - {\rm{j}}\frac{{4\pi {R_0}\left( {{t_m}} \right)}}{\lambda }} \right){{\hat a}_m}\left( k \right)\delta \left( {\tau - k{T_{\rm{s}}}} \right)\\
\quad \quad \quad \quad \cdot \exp \left( { - {\rm{j}}\frac{{4\pi \left( {{y_k} + {x_m}\omega {t_m}} \right)}}{\lambda }} \right)
\end{array}\]
| (17) |
第1个相位相对应目标平动引起的多普勒偏移,与文献[6]中的SAR成像相似,如不考虑相位误差,方位向成像与应用传统信号(LFM或步进频信号)的ISAR成像一样,通过对式(17)中的方位维进行M点FFT, ISAR图像可获得:
|
\[U\left( {\tau ,{f_{\rm{d}}}} \right) = \sum\limits_{m = 0}^{M - 1} {\sum\limits_{k = 0}^{N - 1} {{\hat a}_m}} \left( k \right)\delta \left( {\tau - k{T_{\rm{s}}}} \right) \cdot \delta \left( {{f_{\rm{d}}} - \frac{{2{x_m}\omega }}{\lambda }} \right)\]
| (18) |
回波信号的平动误差已通过包络对齐进行了粗补偿,然而相位校正的准确度要求在波长水平,残余误差不能被忽略。由于平动误差校正的不准确性,不管是RD算法还是本文提出的OFDM-ISAR算法,所得的ISAR图像均有严重的图像模糊,另外,在包络对齐补偿距离偏移$\Delta {h_m}{T_ {\rm s}}$的过程中,我们假设$\Delta {h_m}$为整数来避免IRCI,然而,当距离偏移不是${T_{\rm s}}$的整数倍时,残余的误差也需要被补偿,为从基于CP的OFDM信号中获得聚焦良好的图像,需要相位校正算法补偿复杂的相位误差项。
在移除式(7)中的CP后,信号可以矩阵形式表示为:
其中
AM×N是反射矩阵,其元素对应ISAR目标相应散射中心的后向散射系数,矩阵
|
\[\begin{array}{*{20}{l}}
{E = {\rm{diag}}\left[ {\exp \left( { - {\rm{j}}\frac{{4\pi {R_0}\left[ {m\left( {T + {T_{{\rm{CP}}}}} \right)} \right]}}{\lambda }} \right)} \right]}\\
{\quad = {\rm{diag}}\left[ {\exp \left( {{e_m}} \right)} \right],\;m = 0,1, \cdots ,M - 1}
\end{array}\]
|
对应需要补偿的由目标平动引起的相位误差。大小为
M×
M的矩阵
F= [
F0 F1 $\cdots$
Fm $\cdots$
FM-1]代表方位维傅里叶变换,其中F
m=${\left[ {\exp \left( { - {\rm{j}}2\pi \;\frac{{m \cdot 0}}{M}} \right)\quad \;\exp \left( { - {\rm{j}}2\pi \;\frac{{m \cdot 1}}{M}} \right)\quad \; \cdots \quad \exp \left( { - {\rm{j}}2\pi \frac{{m \cdot \left( {M - 1} \right)}}{M}} \right)\;} \right]^{\rm{T}}}$。结合式(8)和式(10),包络对齐补偿$\Delta {h_m}$后,得到矩阵
S=[
S0 S1 ···
Sn···
SN-1],其中${S_n} = \left[ {\tilde S\left( {{N_{{\rm{CP}}}} + n} \right){\mkern 1mu} {\mkern 1mu} \tilde S\left( {{N_{{\rm{CP}}}} - 1 + n} \right)\:} \right. \cdots \;{\left. {\tilde S\left( {{N_{{\rm{CP}}}} - N + 1 + n} \right)} \right]^{\rm{T}}}$。大小为
M×
N的矩阵
G为已知的回波信号。
通过向量化和Kronecker积[15, 16], 式(19)中的2D模型可转化为下面1D信号模型:
|
\[\begin{array}{l}
g = {S^{\rm{H}}} \otimes \left( {EF} \right)a = \left( {I \otimes E} \right)\left( {{S^{\rm{H}}} \otimes F} \right)a\\
\quad = {Z_E}a
\end{array}\]
| (20) |
其中
g=vec(
G),
a=vec(
A), vec(·)表示矩阵列向量的顺迭,矩阵
I表示大小为
N×
N的单位矩阵。${{I}} \otimes {{E}}$和${{{S}}^{\rm{H}}} \otimes {{F}}$均为大小为
MN×
MN的分块矩阵。
由于矩阵E是未知的,{E, a}的解是无穷的,对a进行准确恢复是一项有挑战性的工作,必须寻找额外信息来获得优化解。由于ISAR目标图像是由强散射构成,强散射点数量远远少于成像平面像素值,所以ISAR图像拥有很强的空间稀疏性,这一性质为恢复ISAR图像提供了重要的先验信息,考虑到噪声影响,图像可通过解决${\ell _1}$范数优化问题解决[13, 14]:
|
\[\left. {\begin{array}{*{20}{c}}
{J\left( {a,E} \right) = \left\| {g{\rm{ - }}{Z_E}a} \right\|_F^2 + \rho {{\left\| a \right\|}_1}}\\
{\left( {a,E} \right){\mkern 1mu} {\mkern 1mu} = \arg \min \left\{ {J\left( {a,E} \right)} \right\}\quad {\rm{ }}}
\end{array}} \right\}\]
| (21) |
式中,${\left\| \cdot \right\|_F}$表示
F矩阵范数,${\left\| \cdot \right\|_1}$表示${\ell _1}$范数。r表示取决于噪声和稀疏性的稀疏系数。式(21)的优化包含两部分:${\left\| a \right\|_1}$部分反映了
a中仅有少数元素是非零的,对应了ISAR图像的稀疏性,$\left\| {{{g}}{\rm{ - }}{{{Z}}_{{E}}}a} \right\|_F^2$对应了噪声抑制项。解决优化式(21)的一个关键问题是确定稀疏系数r,只有合理选择散射系数,才能准确地从OFDM信号中恢复ISAR图像。如果稀疏系数太小,噪声得不到很好地抑制,如果太大,较弱散射点将连同噪声一起被抑制。文献
[13]提供了一种稀疏系数估计方法。为求解优化问题中的未知量
a和
E,这里采用双迭代求解思路。与基于匹配滤波的双重迭代法不同,本文的相位校正算法是基于针对插入CP的OFDM信号的特殊距离像重构方法。测量矩阵
ZE代表了基于CP的OFDM成像的逆过程。为解决${\left\| {\overline {{A}}} \right\|_1}$在原点的不可微性,引入下面的平滑近似:
|
\[{\left\| a \right\|_1} = \sum\limits_{mh = 1}^{MH} {a\left( {mh} \right)} \approx \sum\limits_{mh = 1}^{MH} {{{\left[ {{{\left| {a\left( {mh} \right)} \right|}^2} + \varepsilon } \right]}^{1/2}}} \]
| (22) |
为保证近似有效,$\epsilon $设置为小的正数。这样式(21)中的优化转化为:
|
\[\left. {\begin{array}{*{20}{c}}
{{J_\varepsilon }\left( {a,E} \right) = \left\| {g{\rm{ - }}{Z_E}a} \right\|_F^2}\\
{\; + \rho \sum\limits_{mh = 1}^{MH} {{{\left[ {{{\left| {a\left( {mh} \right)} \right|}^2} + \varepsilon } \right]}^{1/2}}} }\\
{\quad \quad \left( {a,E} \right) = \arg \min \left\{ {J\left( {a,E} \right)} \right\}}
\end{array}} \right\}\]
| (23) |
对式(21)优化求解的一个重要方面在于对{E, $a$}初始化,合适的初始化值可以降低迭代次数,提高算法的准确性,但通常情况下{E, a}的准确先验信息是未知的,与文献[11, 12]中初始化不同,在基于CP的OFDM成像中,初始值a0可通过a0=(ZE0)Hg来形成无IRCI的距离像重构特性。由于无先验信息,相位矩阵E0初始化为I,也就是说(en)0(0≤n≤N-1)。根据OFDM成像步骤,a0的初始化可通过以下步骤实现:(1)移除回波信号的CP并在距离维进行FFT;(2)用每个距离向量除以Wk(k=0, 1, ···, N-1),进行距离向IFFT;(3)对方位维进行FFT。两个未知量a和E的优化求解可利用目标函数对其的导数。在求解a时,在第l次迭代中利用CGA算法[17],Hessian矩阵为:
|
\[H\left( {{a^{l - 1}}} \right){a^l} = {\left( {{Z_{{E^{l - 1}}}}} \right)^{\rm{H}}}g\]
| (24) |
Hessian矩阵的近似求解式为${{H}}\left( a \right) = {\left( {{{{Z}}_{{E}}}} \right)^{\rm{H}}}{{{Z}}_{{E}}} + $ $\rho \cdot {{Λ}} \left( a \right) = {{I}} + \rho \cdot {{Λ}} \left( a \right)$,其中${{Λ}} \left( a \right)$为对角矩阵,可表示为${\rm{diag}}\left\{ {1 / \! \sqrt {|a \! \left( 0 \right) \! {|^2} \! + \! \epsilon} \quad 1 / \! \sqrt {|a \! \left( 1 \right) \! {|^2} \! + \! \epsilon} \quad \ldots } \right. \left. {1/\sqrt {|a\left( {MH - 1} \right){|^2} + \epsilon} } \right\}$。在迭代中,CGA算法可充分利用FFT和Hessian矩阵来提高算法效率。在第
l次迭代中,相位误差可估计为:
|
\[{\left( {{e_n}} \right)^l} = - \angle \left[ {{g^{\rm{H}}}{\rm{vec}}\left[ {\Pi E_n^{l - 1}F{A^l}SI} \right]} \right]\]
| (25) |
其中$\angle \left[\cdot \right]$表示一个复数的角度,$\Pi {{{E}}_n}$是对角矩阵,除了第
n个对角元素外其余对角元素均为零。为了避免上式矩阵运算,提高算法效率,可对矩阵
Al进行方位向IFFT和距离向FFT后,对每一行向量除以${\tilde W_k}$$(k = 0, 1, \cdots, N - 1)$,对所得结果距离维进行IFFT操作并乘以$\Pi {{{E}}_n}_{}^{(w - 1)}$,最后对所得矩阵向量化并与
gH相乘,所得向量元素的角度即为各(e
n)
l的估计值。算法设置迭代终止条件为:
|
\[\frac{{\left\| {{a^{l{\rm{ + }}1}} - {a^l}} \right\|_2^2}}{{\left\| {{a^l}} \right\|_2^2}} \lt \delta \]
| (26) |
其中
d为限定界限。值得注意的是在上述的相位校正过程中,对相位误差的形式是没有要求的,也就是说,此相位校正算法适用于不同类型的相位误差,如由目标平动引起的2次曲线相位误差,由振荡器和子系统不稳定引起的正弦曲线相位误差甚至随机相位误差等。
4 实验验证与分析
雷达仿真信号可根据下列典型的雷达参数产生:PRF=800 Hz,带宽B=370 MHz,中心频率fc=9.6 GHz, OFDM信号采样率为Ts=1/B= 2.7×10-9 s,目标运动角速度为0.03 rad/s。总共有1024个回波脉冲,每个回波脉冲包含N=1024个子载波,距离单元数为512,子载波间隔为Δf=B/N =0.36 MHz,子载波上发射的权向量设为值为-1和1的2次PN码。目标平动速度和加速度分别为100 m/s和5 m/s2,由于平动引起的方位向走动可达127.9 m,相当于距离分辨单元的315倍,由距离偏移引起的频率误差可达1.18 MHz,要远远大于子载波间隔,在OFDM-ISAR成像中要引入运动补偿算法。假设17个散射点均匀分布于距离列中,我们验证CP长度对所提OFDM-ISAR成像算法的影响。
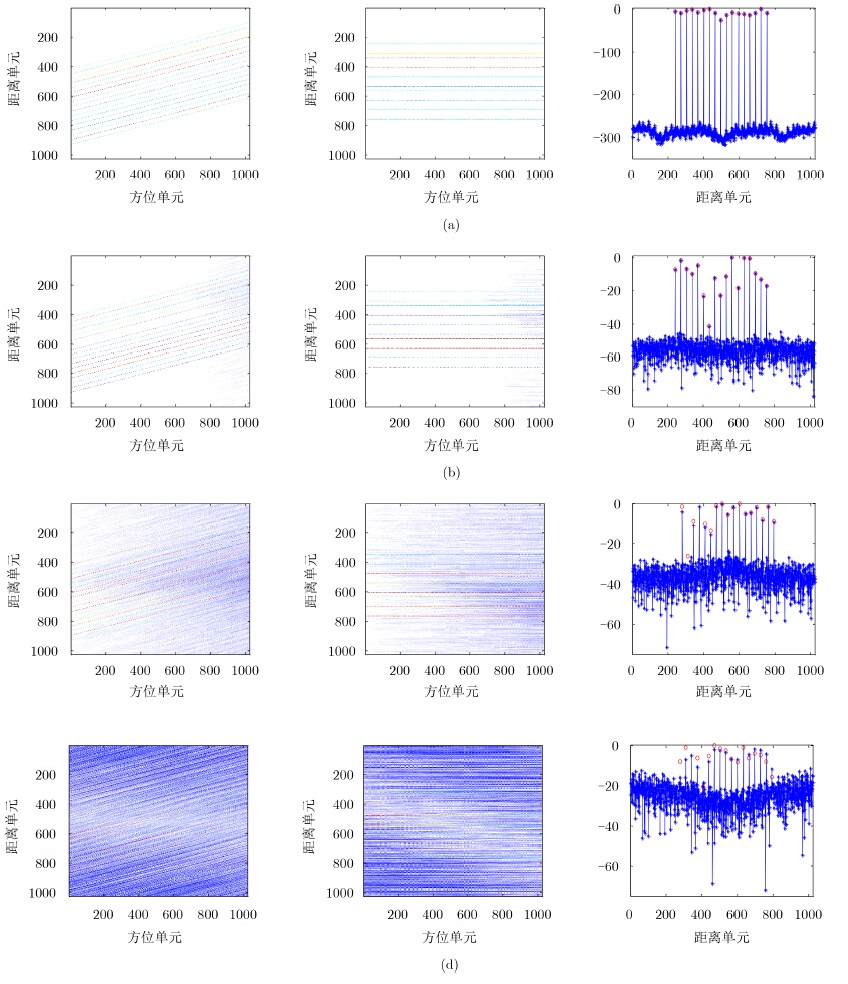
如图 4中红色圆圈所示,17个散射点的幅度是随机产生的,其余距离单元散射点振幅为零,在距离脉压后,不同CP长度的回波OFDM信号如第1列所示,运动目标的走动导致了CPI内距离包络的偏移和检测性能的下降,距离校正算法需对距离偏移误差进行补偿。如第2列所示,利用本文提出的包络对齐方法,可把在同一距离的散射点校正到同一距离单元。为了进一步说明算法的性能,估计的距离列的规范化距离像在第3列用蓝色星线表示,估计所得速度和加速度结果在表 1中列出。图 4和表 1表明,当CP长度为NCP=H+Δhmax-1=826时,所估计得到的点散射点速度、加速度和幅度都比较准确,散射点幅度为零的区域,估计幅度结果低于-270 dB(主要来源于电脑计算误差),随着CP长度的下降,估计的准确性变低,当不考虑距离偏移对CP的影响时,即CP长度为距离单元数512时,估计的准确性进一步变低,IRCI增强,特别地,当CP长度为0时,一些散射点甚至湮没于IRCI中。因此,只有插入足够长度的CP才可以获得无IRCI的ISAR图像。
表 1(Tab. 1)
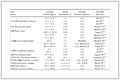
表 1 估计ISAR目标速度和加速度结果
Tab. 1 The estimated velocity and acceleration results
| CP |
826 |
750 |
512 |
0 |
| Velocity (m/s) |
99.9974 |
100.0028 |
99.9969 |
99.9892 |
| Acceleration (m/s2) |
5.034 |
5.065 |
4.892 |
5.127 |
|
表 1 估计ISAR目标速度和加速度结果
Tab. 1 The estimated velocity and acceleration results
|
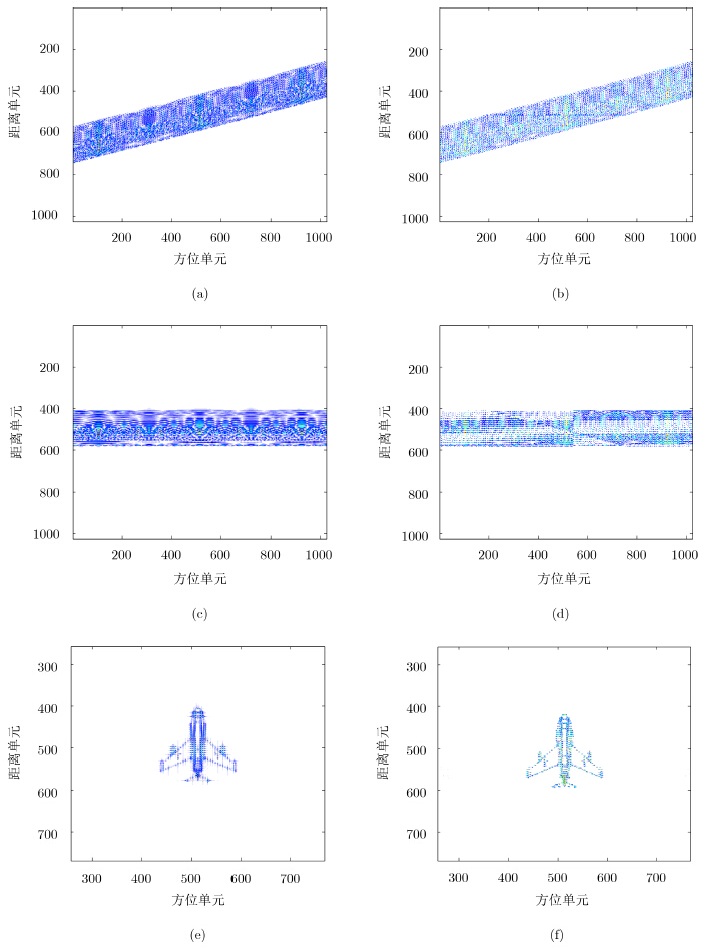
下面,我们验证Yak-42散射模型,进行仿真分析本文算法对OFDM-ISAR成像的运动补偿性能。雷达与目标运动参数均与上面实验一致,应用步进频波形和插入CP的OFDM波形的距离脉压结果分别如图 5(a)和图 5(b)所示,两者均需要运动补偿来校正距离偏移。图 5(a)利用最大相关法和图 5(b)应用修正的最大相关法的包络对齐结果如图 5(c)和图 5(d)所示。为了增加校正的准确性来避免图像模糊,需进一步对误差相位进行校正,图 5(e)和图 5(f)为传统WLSE算法应用到图 5(c)和本文所提算法应用到图 5(d)所得结果,图 5(f)所示结果由于抑制了IRCI,其成像质量远远高于普通算法所得结果。
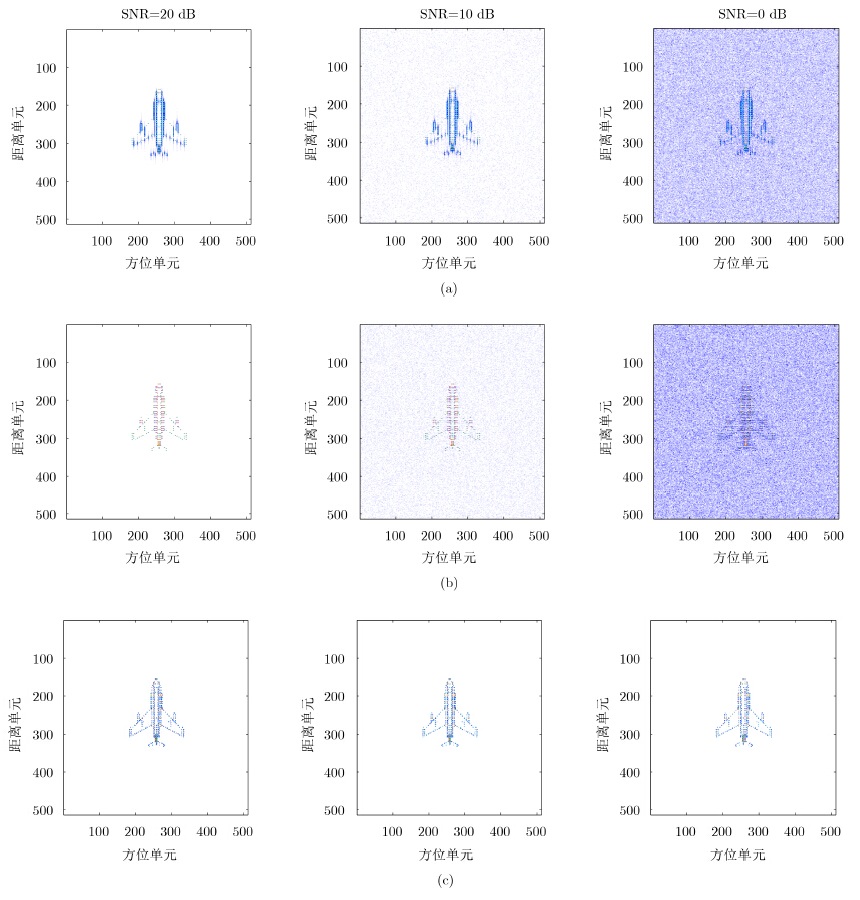
最后,验证噪声对本文算法的影响,假设已通过包络对齐补偿距离偏移,相位误差形式是随机的,由雷达与目标相对速度产生,相对速度范围为-10~10 m/s。步进频波形WLSE算法,插入CP的OFDM波形WLSE算法,插入CP的OFDM波形的本文算法结果分别如图 6(a),图 6(b)和图 6(c)所示。加入高斯白噪声,从左到右SNR为20 dB, 10 dB和0 dB,当SNR较高时,3种算法都可取得较好的相位补偿效果,然而,由于IRCI的存在,步进频波形WLSE算法旁瓣较高,而插入CP的OFDM的WLSE算法和稀疏校正算法抑制了IRCI。尽管插入CP的OFDM的WLSE算法可有效抑制IRCI,但随着噪声的增强,图像湮没在噪声中,而本文所提算法在强噪声环境下依然可以恢复无IRCI距离像并校正相位误差。实验说明了本文算法通过解决稀疏优化问题对相位误差进行校正,具有优越的噪声抑制效果。
5 结束语
本文提出了基于CP的OFDM-ISAR高精度成像算法,通过发射插入足够长度CP的OFDM信号,利用ISAR目标的本质稀疏性,进行联合成像与相位校正,有效实现了精确运动补偿,获得无IRCI的高精度OFDM-ISAR成像。稀疏优化求解算法有效利用了FFT提高运算效率。仿真实验验证了算法有效性。
 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 7)
7) 4)
4) 1)
1) 1)
1) 1)
1) 2)
2) 2)
2) 3)
3) 2)
2) 1)
1) 1)
1) 1)
1)

